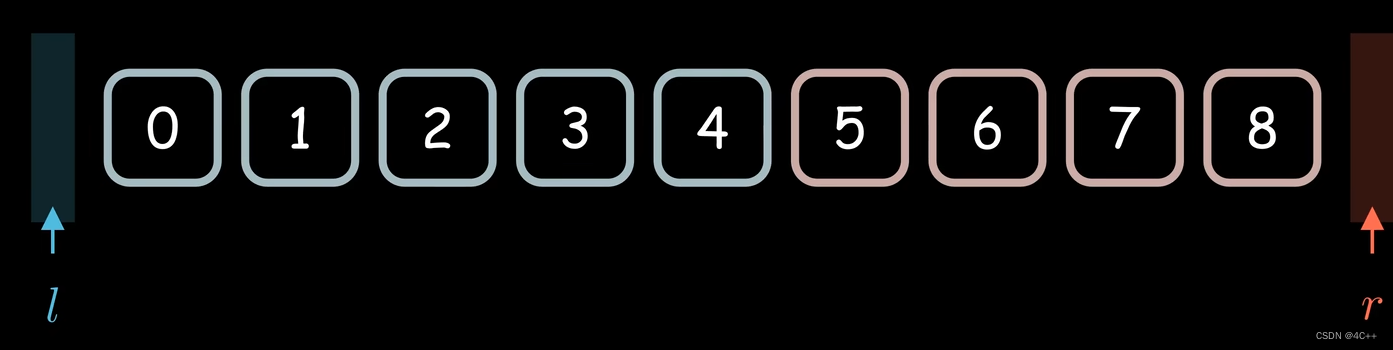目录

一、如何编写二分

二、题目练习

1、二分查找----点击跳转题目

2、在排序数组中查找元素的第⼀个和最后⼀个位置 点击跳转题目

3、搜索插⼊位置----点击跳转题目

4、x的平⽅根----点击跳转题目

5、⼭峰数组的峰顶---点击跳转题目

6、寻找峰值----点击跳转题目

7、搜索旋转排序数组中的最⼩值----点击跳转题目

---

本文使用的方法是基于b站up-- 五点七边 的视频---点击跳转视频

二分算法是一种在有序数组中查找特定元素的高效算法。它的基本思想是通过不断将数组分成两部分，然后比较目标元素与中间元素的大小，从而逐步缩小查找范围，直到找到目标元素或确定目标元素不存在。

二分算法是针对数组的查找算法，要求数组具有单调性，但请不要把单调性简单理解为数字的递增递减，其实只要是数组，无论是什么类型的数组，只要满足单调性，都可以使用二分算法；那究竟这个单调性是什么意思呢？

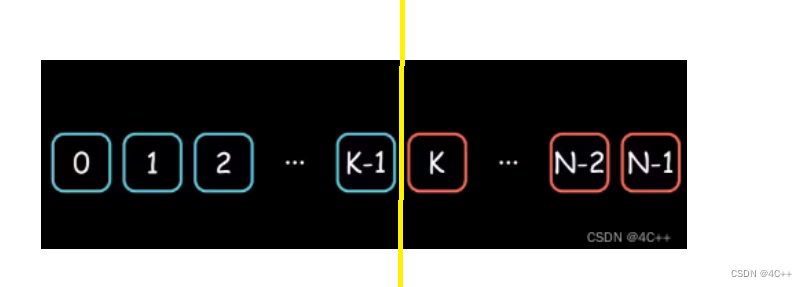
当我们需要在数组中查找某一元素时，如果我们能根据数组和元素的特征，把数组分成两部分，两部分各自持有不同的性质，那么就可以使用二分算法。

红蓝各自代表一种性质，此时，红蓝的边界就是我们查找的元素

一、如何编写二分

我们从前学习的二分算法是定义两个指针l、r，把l~r区间视为有效搜索区间，通过不断的对[l , r]的中点判断性质为缩小l~r区间，当区间长度为1时（l=r）即找到了目标，区间长度为0时（l>r）代表没有符合的目标，但如果按照这种搜索有效区间的思路来编写代码时，在代码的细节问题上总是容易出现边界问题，为了处理各种各样的边界问题，又有几种对应的二分模板；其实如果换一种角度，可以把这些二分模板统一为一个，这篇文章我们换一种角度来编写二分，使得二分算法有且仅有一个统一的模板。

我们暂且把这种方法叫做红蓝染色法：把待搜索的数组看成灰色（待搜索），把我们挖掘出来的性质分别看作红色和蓝色，所谓二分，此时就变成了不断判断数组元素的性质，对数组染色的过程，查找完成时，数组完全被红色、蓝色占据，红蓝边界即为查找结果。

此时再理解二分，其实就是想象一个挡板（黄色），把数组分为两部分（蓝、红），通过不断的迭代，l会移动到黄色的左边，r会移动到黄色的右边，再根据题意酌情返回l或者r。

伪代码如下：

l=-1, r=N  //在(l,r)的数组索引开区间内，数组元素都是灰色的while l+1≠r  //l+1=r时，蓝红区域接触m = ⌊(l+r)/2⌋  //开区间中间元素if IsBlue(m)l=m  //蓝色区域向右拓展到中间元素elser=m  //红色区域向左拓展到中间元素//根据实际情况返回l或r，但要注意：返回谁就要对谁做越界判断！
return l or r  

需要注意的是，一开始定义l、r指针时，它们是指向数组外的，这样才能代表数组是灰色待搜索的，也就是刚开始蓝色区域、红色区域在数组索引区域外，因为数组区域可能全蓝或全红，为保证考虑到所有情况不得不这么做。

二、题目练习

1、二分查找----点击跳转题目

题意：在单调递增的数组中查找值为target，可能不存在target

思考：把数组以target分割，左边元素的性质为：小于等于target；右边元素的性质为：大于target；最后找到的分界线中，左边为l，右边为r，如果l位置的元素不等于target则数组中没有值为target的元素

class Solution {
public:int search(vector<int>& nums, int target) {int l = -1, r = nums.size();while(l+1 < r){int mid = l + r >> 1;if(nums[mid] <= target)l = mid;elser = mid;}//引用l、r前需要判断是否为合法下标if( l == -1 || nums[l] != target) return -1;else return l;}
};

2、在排序数组中查找元素的第⼀个和最后⼀个位置 点击跳转题目

二分两次，分别找到红色、黄色的划分挡板

代码：

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int l = -1, r = nums.size();int ret1,ret2;if(r == 0) return {-1,-1};while(l +1 < r){int mid = l + r >> 1;if(nums[mid] < target)l = mid;elser = mid;}if(l+1 >= nums.size() || nums[l+1] != target) return {-1,-1};ret1 = l + 1;l = -1, r = nums.size();while(l +1 < r){int mid = l + r >> 1;if(nums[mid] <= target)l = mid;elser = mid;}ret2 = l;return {ret1,ret2};}
};

3、搜索插⼊位置----点击跳转题目

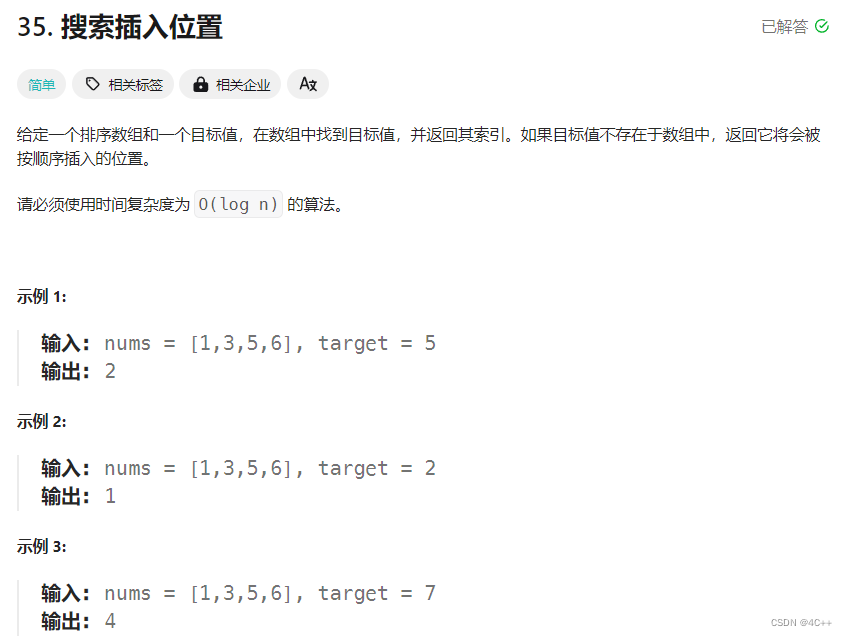
以小于等于target为标准划分数组，对比l指向的元素是否为target

代码：

class Solution {
public:int searchInsert(vector<int>& nums, int target) {int l = -1 ,r = nums.size();while(l + 1 < r){int mid = l + r >> 1;if(nums[mid] <= target)l = mid;elser = mid;}int index = 0;if(l == -1 ) index = 0;else if(nums[l] != target) index = l + 1;else index = l;return index;}
};

4、x的平⽅根----点击跳转题目

对0~INT_MAX做二分，挡板左边：平方小于等于x；挡板右边：平方大于x

代码：

class Solution {
public://l: l^2 <= x//r: r^2 > xint mySqrt(int x) {int l = -1, r = INT_MAX;while(l + 1 < r){//做平方时防止溢出long long mid = l + r >> 1;if(mid*mid <= x)l = mid;elser = mid;}if(l==-1) return 0;else return l;}
};

5、⼭峰数组的峰顶---点击跳转题目

以山峰元素的右侧为挡板

挡板左侧：arr[i-1] < arr[i]

挡板右侧：arr[i-1] > arr[i]

代码：

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {//l：arr[l] < arr[l+1] //r: arr[r] > arr[r+1] //返回rint l = -1, r = arr.size();while(l + 1 < r){int mid = l + r >> 1;if(arr[mid] < arr[mid+1])l = mid;elser = mid;}return r;}
};

6、寻找峰值----点击跳转题目

观察可知，峰值元素的左侧满足递增、右侧满足递减；由于是返回任意峰值，所以和上一题一样；

挡板左侧：arr[i-1] < arr[i]

挡板右侧：arr[i-1] > arr[i]

代码：

class Solution {
public:int findPeakElement(vector<int>& nums) {int l = -1, r = nums.size();while(l +1 < r){int mid = l + r >> 1;if(mid-1 >= 0){if(nums[mid-1] < nums[mid])l = mid;elser = mid;}else    l = mid;//数组越界时说明在比较nums[-1]和nums[0]}return l;}
};

7、搜索旋转排序数组中的最⼩值----点击跳转题目

由于数组是由单调递增的数组旋转得到，那么得到的数组满足左侧区间永远大于右侧区间

以最小值左侧为挡板，取数组最后一个值x来比较（因为他是第二段区间的最大值）

挡板左侧：左侧元素 > x

挡板右侧：右侧元素 <= x (因为右侧区间可能只有一个元素，所以取等)

代码：

class Solution {
public:int findMin(vector<int>& nums) {int l = -1, r = nums.size();int x = nums[r-1];while(l + 1 < r){int mid = l + r >> 1;if(nums[mid] > x)l = mid;elser = mid;}return nums[r];}
};

8、点名----点击跳转题目

数组中记录的是未缺勤的学生，通过观察我们发现，如果所有学生都未缺勤，那么数组下标就会和学号正好相等，那么在点名还没点到缺勤学生时，这个性质依然成立，以缺勤学生本该在的位置为挡板：

挡板左侧：数组下标 等于 对应元素

挡板右侧：数组下标 不等于 对应元素

代码：

class Solution {
public:int takeAttendance(vector<int>& records) {//l:下标和值相等 r：下标和值不想等int l = -1, r= records.size();while(l + 1 < r){int mid = l + r >> 1;if(records[mid] == mid)l = mid;elser = mid;}return l+1;}
};

通过以上题目的练习我们发现，⼆分的本质：找到⼀个判断标准，使得查找区间能够⼀分为⼆，分界中存在一个挡板，挡板左侧为l，挡板右侧为r