Basic radiometry

辐射度量学

之前实现过Blinn-Phong model

你认为Whitted-style的光线追踪会给你正确的结果吗？

路径追踪的基础

照明测量系统和单位
精确测量光的空间特性
新术语：辐射通量，强度，辐照度，辐射度
Radiant flux, intensity, irradiance, radiance

以物理正确的方式进行照明计算

辐射能和通量（功率）Radiant Energy and Flux (Power)

定义：辐射能(Radiant energy)是电磁辐射的能量。它的单位是焦耳，用符号表示
$$Q[J=Joule]$$
定义：辐射通量（功率）Radiant flux (power)是单位时间内发射、反射、发射或接收的能量
$$\Phi =\frac{dQ}{dt}[W=Watt][lm=lumen{]}^{\ast }$$
通量-#在单位时间内流过传感器的光子数

重要的光测量

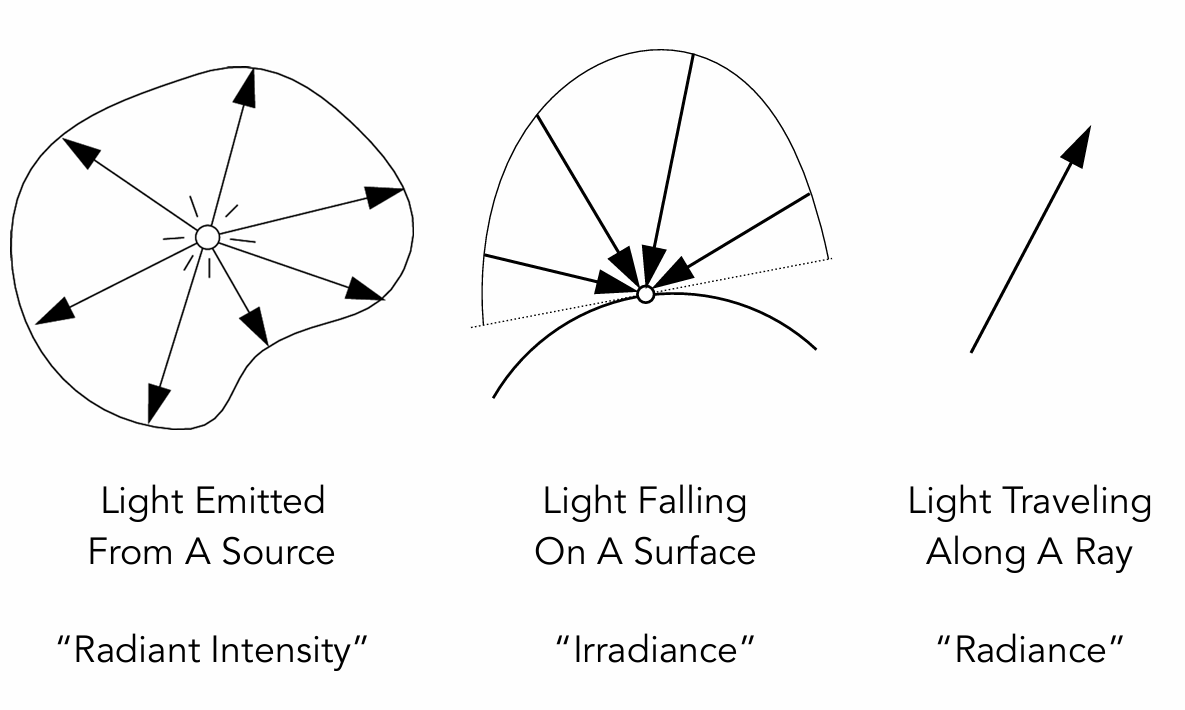
辐射强度 Radiant Intensity

定义：辐射（发光）强度是点光源单位solid angle立体角（?）发出的功率。
$$I(\omega )=\frac{d\Phi }{d\omega }$$
$$[\frac{W}{sr}][\frac{lm}{sr}=cd=candela]$$
坎德拉是国际单位制的七个基本单位之一。

角和立体角
角：圆上的弧长与半径之比

• $\theta =\frac{l}{r}$
• 圆有$2\pi$弧度
  

立体角：球面上的面积与半径的平方之比

• $\Omega =\frac{A}{r^2}$
• 球面$4\pi$球面度
  

微分立体角
$$dA=(rd\theta )(r\sin \theta d\varphi )=r^2\sin \theta d\theta d\varphi$$
$$d\omega =\frac{dA}{r^2}=\sin \theta d\theta d\varphi$$

球面：$S^2$
$$\Omega ={\int }_{S^2}d\omega ={\int }_0^{2\pi }{\int }_0^{\pi }\sin \theta d\theta d\varphi =4\pi$$
$\omega$是一个方向向量
将使用$\omega$表示方向矢量(单位长度

各向同性点源

$$\Phi ={\int }_{S^2}Id\omega =4\pi I$$
$$I=\frac{\Phi }{4\pi }$$

现代LED灯

辐照度Irradiance

定义：辐照度是入射到表面点上的单位面积的功率。

$$E(x)=\frac{d\Phi (x)}{dA}$$
$$[\frac{W}{m^2}]=[\frac{lm}{m^2}=lux]$$

朗伯余弦定律Lambert’s Cosine Law

表面的辐照度正比于光方向与表面法线夹角的余弦。
$$E=\frac{\Phi }{A}\cos \theta$$
其中$\cos \theta =l\cdot n$

Radiance辐亮度

辐射度是描述光在环境中分布的基本场量

• 亮度是与射线有关的量
• 渲染就是计算亮度

定义：辐射度（亮度）是一个表面在单位立体角、单位投影面积上发射、反射、传输或接收的功率。

$$L(p,\omega )=\frac{d^2\Phi (p,w)}{d\omega dA\cos \theta }$$

$$[\frac{W}{sr{m}^2}][\frac{cd}{m^2}=\frac{lm}{sr{m}^2}=nit]$$

单位投影面积上单位立体角的功率。

Incident Radiance入射辐亮度

入射辐射度是到达表面的单位立体角的辐射度
$$L(p,\omega )=\frac{dE(p)}{d\omega \cos \theta }$$
它是沿着给定光线到达表面的光。点在表面和入射方向

Exiting Radiance出射辐亮度

出射辐射度是离开表面的单位投影面积的强度。
$$L(p,\omega )=\frac{dI(p,\omega )}{dA\cos \theta }$$
对于面积光，它是沿着给定光线发出的光（指向表面和出口方向）。

辐照度：面积dA所接收的总功率

辐亮度：面积dA从“方向”dw接收的功率
$$dE(p,\omega )=L_i(p,\omega )\cos \theta d\omega$$

$$E(p)={\int }_{H^2}{L}_i(p,\omega )\cos \theta d\omega$$

单位半球:$H^2$

双向反射分布函数 Bidirectional Reflectance Distribution Function (BRDF)

一点的反射

从${\omega }_i$方向发出的辐射转化为dA接收的功率E

功率E就变成了任意方向上的辐照度${\omega }_0$

微分辐照度入射：$dE({\omega }_i)=L({\omega }_i)\cos {\theta }_{i}d{\omega }_i$

微分辐亮度射出：$d{L}_r({\omega }_r)$

双向反射分布函数（BRDF）表示从每个入射方向反射到每个出射方向${\omega }_r$的光量

$$f_r({\omega }_i\to {\omega }_r)=\frac{d{L}_r({\omega }_r)}{d{E}_i({\omega }_i)}=\frac{d{L}_r({\omega }_r)}{L_i({\omega }_i)\cos {\theta }_{i}d{\omega }_i}[\frac{1}{sr}]$$

反射方程

$$L_r(p,{\omega }_r)={\int }_{H^2}{f}_r(p,{\omega }_i\to {\omega }_r)L_i(p,{\omega }_i)\cos {\theta }_{i}d{\omega }_i$$

挑战：递归方程

反射辐照取决于入射辐照

但是入射的辐照取决于反射的辐照（在场景的另一点）

任何一个出射的点都可能作为其他点的入射

渲染方程

通过添加一个发射项来使反射方程具有普遍性
$$L_r(p,{\omega }_r)=L_e(p,{\omega }_o)+{\int }_{{\Omega }^{+}}{f}_r(p,{\omega }_i,{\omega }_o)L_i(p,{\omega }_i)(n\cdot {\omega }_i)d{\omega }_i$$
自身发射的光。注意：现在，我们假设所有方向是向外的！

一个点光源

一堆点光源

面光源

光源可能是反射来的

Kajiya 86

是第二类Fredholm积分方程[广泛的数值研究]以标准形式
$$I(u)=e(u)+\int I(v)K(u,v)dv$$
线性算子方程

$K(u,v)$方程的核，光转移算子
$$L=E+KL$$
可以离散成一个简单的矩阵方程[或联立线性方程组](L， E为矢量，K为光转移矩阵

光线追踪和拓展

• 通用类数值蒙特卡罗方法

• 场景中所有光线路径的近似集合

$$L=E+KL$$

$$(I-K)L=E$$

$$L=(I-K{)}^{-1}E$$

$$L=(I+K+K^2+...)E$$

$$L=E+EK+E{K}^2+E{K}^3+,,,$$

$E$: 直接从光源发出的光

$KE$: 表面直接照明

以上两个：光栅化中的着色

$K^{2}E$: 间接照明（一次间接反弹）(镜子,折射)

$K^{3}E$：两次反弹

加起来：全局光照