线性方程组

考虑线性方程组， 已知 $A\in {\mathbb{R}}^{n,n},b\in {\mathbb{R}}^n$， 求未知 $x\in {\mathbb{R}}^n$

$$A_{1,1}{x}_1+A_{1,2}{x}_2+\cdots +A_{1,n}{x}_n=b_1,$$
$$A_{2,1}{x}_1+A_{2,2}{x}_2+\cdots +A_{2,n}{x}_n=b_2,$$
$$\cdots$$
$$A_{n,1}{x}_1+A_{n,2}{x}_2+\cdots +A_{n,n}{x}_n=b_n,$$

也可以写为矩阵乘法的形式，
$$Ax=b$$

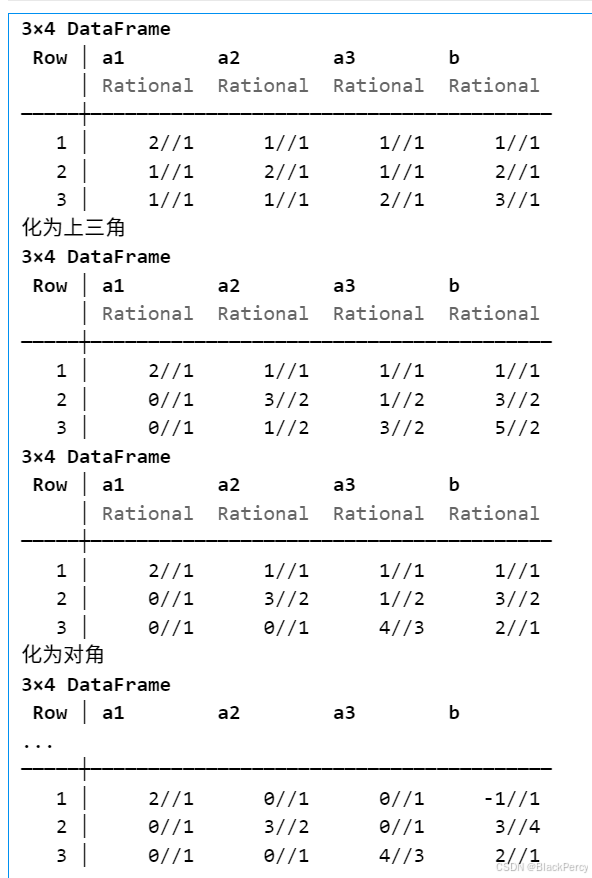
化为上三角

• 第 1 轮:
  $$A_{i,1:n}=A_{i,1:n}-\frac{A_{i,1}}{A_{1,1}}{A}_{1,1:n},i=2,\cdots ,n$$

• 第 2 轮:
  $$A_{i,2:n}=A_{i,2:n}-\frac{A_{i,2}}{A_{2,2}}{A}_{2,2:n},i=3,\cdots ,n$$
  $\cdots$

• 第 k 轮:
  $$A_{i,k:n}=A_{i,k:n}-\frac{A_{i,k}}{A_{k,k}}{A}_{k,k:n},i=k+1,\cdots ,n$$

• 第n-1 轮
  $$A_{i,n-1:n}=A_{i,n-1:n}-\frac{A_{i,n-1}}{A_{n-1,n-1}}{A}_{n,n-1:n},i=n$$

化为对角

• 第 1 轮:
  $$A_{i,2:n}=A_{i,2:n}-\frac{A_{i,n}}{A_{n,n}}{A}_{n,2:n},i=1,\cdots ,n-1$$

• 第 2 轮:
  $$A_{i,2:n-1}=A_{i,2:n-1}-\frac{A_{i,n-1}}{A_{n-1,n-1}}{A}_{n-1,2:n-1},i=1,\cdots ,n-2$$
  $$\cdots$$

• 第 k 轮:
  $$A_{i,2:n-k+1}=A_{i,2:n-k+1}-\frac{A_{i,n-k+1}}{A_{n-k+1,n-k+1}}{A}_{n-k+1,2:n-k+1},i=1,\cdots ,n-k+1$$

• 第n-1 轮

$$A_{i,2}=A_{i,2}-\frac{A_{i,2}}{A_{2,2}}{A}_{2,2},i=1$$

美化数据格式

julia">using DataFrames
function pm(A,b)m,n=size(A); z=[]for i=1:nz=[z; "a$i"]endz=[z; "b"]println(DataFrame([A b],z))
end            

高斯消元法程序

julia">function LEsol(A,b,SHOW=false)"""SHOW 默认为 false 不输出解题步骤, 可以选填 true 输出解题步骤"""n=length(b);   A=copy(A);  b=copy(b)if SHOW pm(A,b) endif SHOW println("化为上三角") endfor i=1:n-1for j=i+1:nc=A[j,i]/A[i,i]b[j]=b[j]-b[i]*cA[j,i:n]=A[j,i:n]-A[i,i:n]*c endif SHOW pm(A,b) endendif SHOW println("化为对角") endfor i=n:-1:2for j=1:i-1c=A[j,i]/A[i,i]b[j]=b[j]-b[i]*cA[j,i:n]=A[j,i:n]-A[i,i:n]*cendif SHOW pm(A,b) endendx=copy(b)for j=1:nx[j]=b[j]/A[j,j];endreturn(x)
end

举例

julia">n=3;
A=ones(Rational,n,n)
b=ones(Rational,n)
for i=1:n-1A[i,i]=2.0;A[i,i+1]=1.0;A[i+1,i]=1.0; b[i]=i+0.0
end
A[n,n]=2.0;
b[n]=n;
x=LEsol(A,b,true)

求解结果