Adam是一种自适应学习率的优化算法,结合了动量和自适应学习率的特性。
主要思想是根据参数的梯度来动态调整每个参数的学习率。
核心原理包括:
-
动量(Momentum):Adam算法引入了动量项,以平滑梯度更新的方向。这有助于加速收敛并减少震荡。
-
自适应学习率:Adam算法计算每个参数的自适应学习率,允许不同参数具有不同的学习速度。
-
偏差修正(Bias Correction):Adam算法在初期迭代中可能受到偏差的影响,因此它使用偏差修正来纠正这个问题。
Adam相关公式
初始化:
-
参数:
-
学习率:
-
梯度估计的移动平均(一阶矩):
-
梯度平方的移动平均(二阶矩):
-
时间步数:
每个迭代步骤:
-
计算梯度:
-
更新一阶矩:
-
更新二阶矩:
-
修正偏差(Bias Correction):
和
-
更新参数:
,其中
是一个小的常数,以防分母为零。
项目:基于Adam优化算法的神经网络训练
在这个项目中,我们将使用Adam优化算法来训练一个简单的神经网络,以解决二分类问题。我们将深入讨论Adam算法的原理和公式,并展示如何在Python中实施它。最后,我们将绘制学习曲线,以可视化模型的训练进展。
项目:基于Adam优化算法的神经网络训练
在这个项目中,我们将使用Adam优化算法来训练一个简单的神经网络,以解决二分类问题。我们将深入讨论Adam算法的原理和公式,并展示如何在Python中实施它。最后,我们将绘制学习曲线,以可视化模型的训练进展。
模型训练
使用Python代码实现Adam算法来训练一个二分类的神经网络。
使用Python中的NumPy库来进行计算,并使用一个合成的数据集来演示。
import numpy as np
import matplotlib.pyplot as plt# 定义模型和数据
np.random.seed(42)
X = np.random.rand(100, 2) # 特征数据
y = (X[:, 0] + X[:, 1] > 1).astype(int) # 二分类标签# 定义神经网络模型
def sigmoid(x):return 1 / (1 + np.exp(-x))def predict(X, weights):return sigmoid(np.dot(X, weights))# 初始化参数和超参数
theta = np.random.rand(2) # 参数初始化
alpha = 0.1 # 学习率
beta1 = 0.9 # 一阶矩衰减因子
beta2 = 0.999 # 二阶矩衰减因子
epsilon = 1e-8 # 用于防止分母为零# 初始化Adam算法所需的中间变量
m = np.zeros(2)
v = np.zeros(2)
t = 0# 训练模型
num_epochs = 100
for epoch in range(num_epochs):for i in range(len(X)):t += 1gradient = (predict(X[i], theta) - y[i]) * X[i]m = beta1 * m + (1 - beta1) * gradientv = beta2 * v + (1 - beta2) * gradient**2m_hat = m / (1 - beta1**t)v_hat = v / (1 - beta2**t)theta -= alpha * m_hat / (np.sqrt(v_hat) + epsilon)# 输出训练后的参数
print("训练完成后的参数:", theta)# 定义损失函数
def loss(X, y, weights):y_pred = predict(X, weights)return -np.mean(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))# 记录损失值
loss_history = []
for i in range(len(X)):loss_history.append(loss(X[i], y[i], theta))# 绘制损失函数曲线
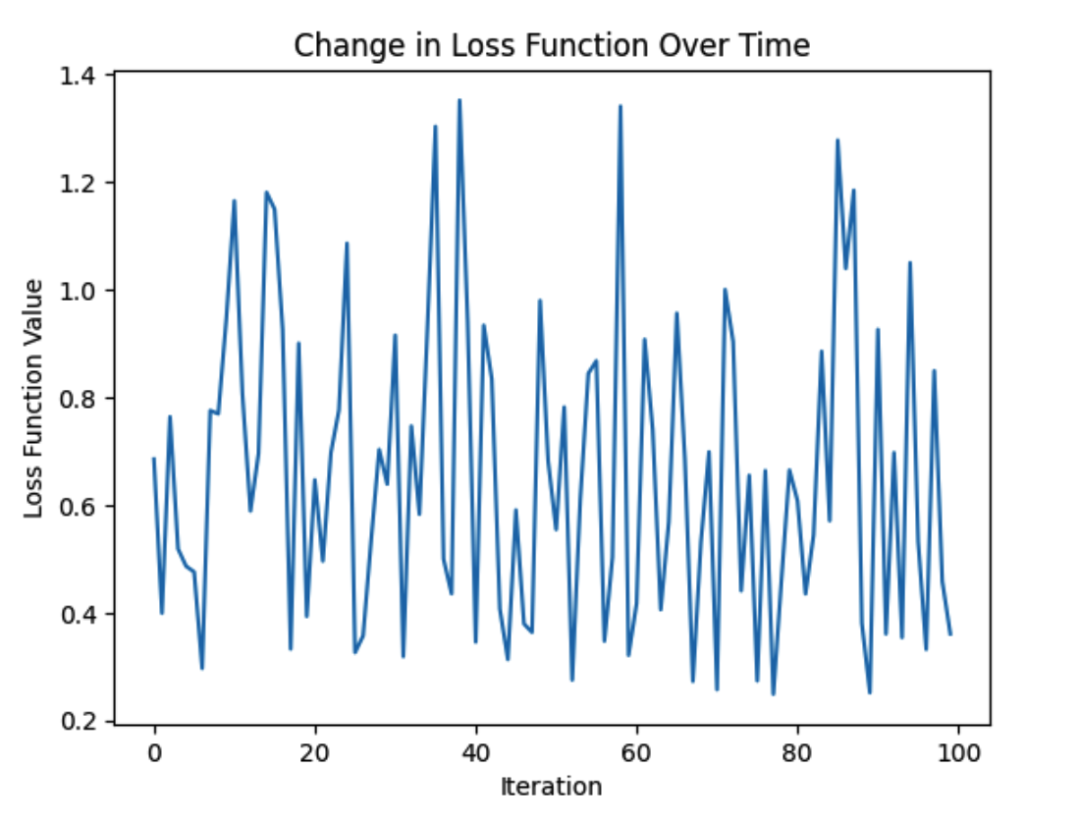
plt.plot(range(len(X)), loss_history)
plt.xlabel("Iteration")
plt.ylabel("Loss Function Value")
plt.title("Change in Loss Function Over Time")
plt.show()
这个图形将显示损失函数值随着迭代次数的减小而减小,这表明Adam优化算法成功地训练了模型。