🔒文章目录:
1.❤️❤️前言~🥳🎉🎉🎉
2.栈的应用场景
2.1逆序打印链表
2.2逆波兰表达式求值
2.3括号匹配
2.4出栈入栈次序匹配
2.5最小栈
3. 栈 虚拟机栈 栈帧的区别
4.总结
1.❤️❤️前言~🥳🎉🎉🎉
Hello, Hello~ 亲爱的朋友们👋👋,这里是E绵绵呀✍️✍️。
如果你喜欢这篇文章,请别吝啬你的点赞❤️❤️和收藏📖📖。如果你对我的内容感兴趣,记得关注我👀👀以便不错过每一篇精彩。
当然,如果在阅读中发现任何问题或疑问,我非常欢迎你在评论区留言指正🗨️🗨️。让我们共同努力,一起进步!
加油,一起CHIN UP!💪💪
🔗个人主页:E绵绵的博客
📚所属专栏:1. JAVA知识点专栏
深入探索JAVA的核心概念与技术细节
2.JAVA题目练习
实战演练,巩固JAVA编程技能
3.c语言知识点专栏
揭示c语言的底层逻辑与高级特性
4.c语言题目练习
挑战自我,提升c语言编程能力
📘 持续更新中,敬请期待❤️❤️

2.栈的应用场景
2.1逆序打印链表
一般我们可以用递归去逆序打印链表。
// 递归方式 void printList(Node head){if(null != head){printList(head.next);System.out.print(head.val + " ");} }
除此之外我们还可以用另一种特殊方法,就是利用栈去打印,代码展示在这。相比递归其更高效。
// 循环方式 void printList(Node head){if(null == head){return;}Stack<Node> s = new Stack<>();// 将链表中的结点保存在栈中Node cur = head;while(null != cur){s.push(cur);cur = cur.next;}// 将栈中的元素出栈while(!s.empty()){System.out.print(s.pop().val + " ");} }
2.2逆波兰表达式求值
题目描述:
给你一个字符串数组
tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式,返回一个表示表达式值的整数。
- 注意:两个整数之间的除法只保留整数部分。
- 可以保证给定的逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 :
输入:tokens = ["2","1","+","3","*"] 输出:9 解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
🍓逆波兰表达式:逆波兰表达式是一种后缀表达式,所谓后缀就是指运算符写在后面
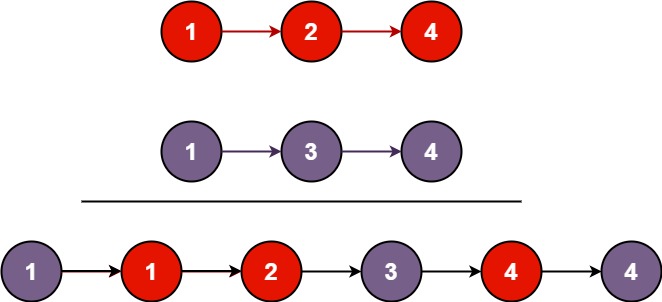
- 平常使用的算式则是一种中缀表达式,如 ( 1 + 2 ) * ( 3 + 4 ) 。
- 该算式的逆波兰表达式写法为 1 2 + 3 4 + * 。
✨前、中、后缀表达式的转换:
- 将中缀表达式按运算顺序加上括号,从左到右分别将运算符移到对应括号的最右边,再去掉所有括号,就能得到后缀表达式。
- 同理将运算符移到对应括号的最左边就得到了前缀表达式。
🌌逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
- 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
所以我们可以根据其第二个优点作为思路去求逆波兰表达式的值
⏳解题思路:
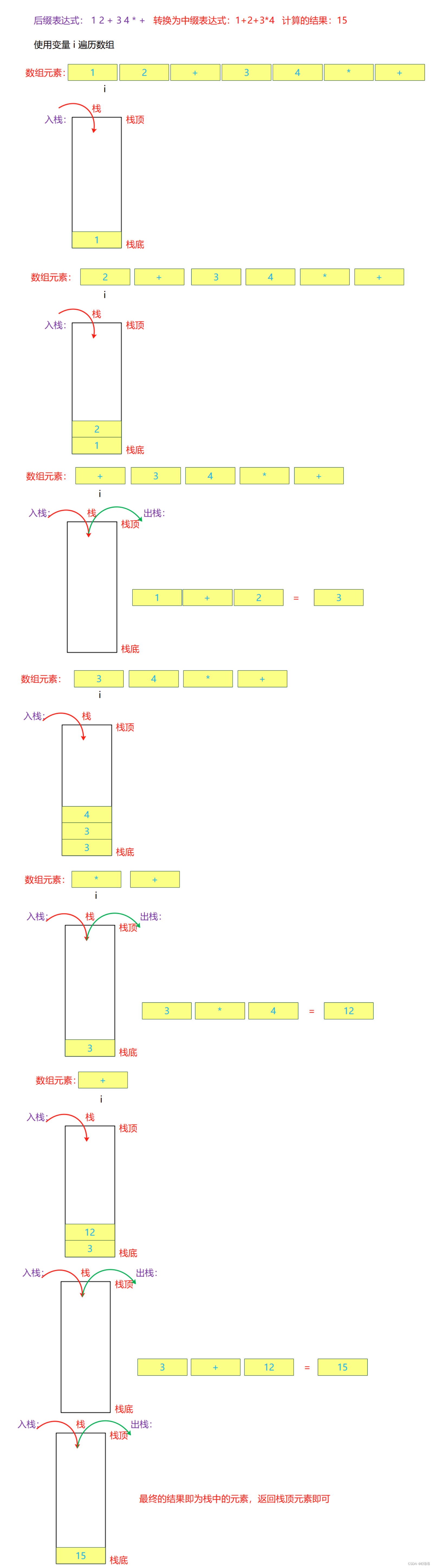
1.创建一个存放整型数据的栈。遍历字符串数组,遇到数字就入栈。遇到运算符则取出栈顶的两个元素进行计算,再将计算后的结果入栈。
2.写一个方法isOperation(),判断字符串数组中的字符是不是运算符。
3.遍历字符串数组,调用isOperation()方法。如果当前字符不是运算符,则将字符转换为对应的十进制整数并入栈。如果当前字符是运算符则取出两个元素进行计算(出栈)。再计算后的结果入栈。
需要注意:先出栈的元素放到运算符的右边,后出栈的元素放到运算符的左边。
最终栈顶元素的值为计算的结果,返回栈顶元素即可。
完整代码及测试 :
public class Test1 {public static void main(String[] args) {String[] a={"1","2","+","3","4","*","+"};Solution solution=new Solution();System.out.println( solution.evalRPN(a));}}class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack=new Stack();int a=0;for(;a<tokens.length;a++){if(checkDo(tokens[a])==true){switch(tokens[a]){case "+":stack.push(stack.pop()+stack.pop());break;case "-":int b=stack.pop();int c=stack.pop();stack.push(c-b);break;case "*":stack.push(stack.pop()*stack.pop());break;case "/":int g=stack.pop();int f=stack.pop();stack.push(f/g);break;}}else{stack.push(Integer.parseInt(tokens[a]));}}return stack.pop();}public Boolean checkDo(String a){if(a.equals("+")||a.equals("-")||a.equals("/")||a.equals("*")){return true;}return false;}
}
该题链接:逆波兰表达式求值
2.3括号匹配
📌题目描述:
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
📋题目示例:
示例1:
输入:s = "()[]{}"
输出:true
示例2:
输入:s = "([)]"
输出:false
⏳解题思路:
1.创建一个存放字符数据的栈。遍历字符串,使用charAt()方法获取字符串中的每一个字符。
如果字符是左括号就进行入栈操作(左括号:'(' , '[' , '{' )。
1.分析括号不匹配的情况有三种:左括号多:((((( )))
右括号多:((( )))))
左右括号次序不匹配:( [ ) ]
2.不匹配:因为栈当中存储的是左括号,如果当 i 遍历完整个字符串,栈还是不为空,那么就是左括号多。返回false。
如果当前字符是右括号,且栈为空,那么就是右括号多,返回false。
如果当前字符是右括号,栈顶元素与当前的右括号字符不匹配,返回false。
3.匹配:( [ ] )如果字符是右括号,判断栈顶元素与当前的右括号字符是否匹配,如果匹配就进行出栈操作,直到遍历完整个字符串,且我们的栈为空则返回true。
完整代码及测试如下:
import java.util.*;
public class Test2 {public boolean isValid(String s) {Stack<Character> stack=new Stack<>();for(int a=0;a<s.length();a++){char i=s.charAt(a);if(i=='{'||i=='('||i=='[')stack.push(i);else{if(stack.empty()==true)return false;if((stack.peek()=='('&&i==')')||(stack.peek()=='{'&&i=='}')||(stack.peek()=='['&&i==']'))stack.pop();elsereturn false;}}if(stack.empty()!=true)return false;elsereturn true;}public static void main(String[] args) {Test2 test2=new Test2();System.out.println(test2.isValid("{{{}}}([])"));}}
该题链接:括号匹配
2.4出栈入栈次序匹配
📌题目描述:
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
0<=pushV.length == popV.length <=1000
-1000<=pushV[i]<=1000
pushV 的所有数字均不相同
📋题目示例:
输入:[1,2,3,4,5],[4,5,3,2,1]
返回值:true
说明:
可以通过 push(1)=>push(2)=>push(3)=>push(4)=>pop()=>push(5)=>pop()=>pop()=>pop()=>pop()
这样的顺序得到[4,5,3,2,1]这个序列,返回true
⏳解题思路:
- 首先,遍历第一个序列,将第一个序列的第一个元素压入栈中;
- 遍历第二个序列,每次判断当前栈顶元素是否与第二个序列的当前元素相同;
- 如果相同,则弹出栈顶元素,并且将第二个序列的指针向后移动一位;而后重复第二个步骤的判断。
- 如果不同,则继续将第一个序列的元素压入栈中,直到找到一个与第二个序列当前元素相同的栈顶元素为止,或者直至循环结束;
- 最后,如果栈为空,则说明第二个序列是第一个序列的一个合法的弹出顺序,返回true;否则,返回false
完整代码及测试如下:
public class Test4 {public static void main(String[] args) {int[] pushV={1,2,3,4,5};int[] popV={4,5,3,2,1};Main main=new Main();System.out.println(main.IsPopOrder(pushV, popV));}}class Main {public boolean IsPopOrder (int[] pushV, int[] popV) {Stack<Integer> stack=new Stack<>();int j=0;for(int i=0;i<pushV.length;i++){stack.push(pushV[i]);while(!stack.empty()&&popV[j]==stack.peek()){j++;stack.pop();}}if(stack.empty())return true;elsereturn false;}
}
该题链接:出栈入栈次序匹配
2.5最小栈
📌题目描述
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
📋题目示例:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
⏳解题思路:
创建两个栈,一个普通栈,一个最小栈。
入栈:
所有元素都要放入普通栈,判断元素是否放入最小栈,如果最小值为空,则直接将元素入最小栈。如果最小栈中有元素,将待入栈元素与最小栈的栈顶元素进行比较,如果待入栈元素小于或等于最小栈中的栈顶元素,则将元素也放入最小栈,否则就不放入最小栈。
出栈:普通栈中的元素都要进行出栈操作。如果最小栈的栈顶元素等于普通栈的栈顶元素,那么最小栈也进行出栈操作,否则最小栈中的元素不出栈。
返回值:top()方法返回普通栈中的栈顶元素
getMin()方法返回最小栈的栈顶元素
完整代码及测试如下:
public class Test3 {public static void main(String[] args) {MinStack minStack=new MinStack();minStack.push(512);minStack.push(-1024);minStack.push(-1024);minStack.push(512);minStack.pop();minStack.pop();minStack.pop();System.out.println(minStack.getMin());}}
class MinStack {Stack<Integer> stack=new Stack<>();Stack<Integer> minStack=new Stack<>();public MinStack() {;}public void push(int val) {stack.push(val);if(minStack.empty())minStack.push(val);else{if(val<=minStack.peek())minStack.push(val);}}public void pop() {if(stack.pop().equals(minStack.peek()))minStack.pop();}public int top() {return stack.peek();}public int getMin() {return minStack.peek();}
}
该题链接:最小栈
3. 栈 虚拟机栈 栈帧的区别
栈是一种特殊的数据结构,它具有“先进后出”的特点,栈可以通过入栈(push)和出栈(pop)操作进行数据的存储和读取。
虚拟机栈是Java虚拟机所使用的栈结构,用于存储方法执行时的数据和指令等信息。在Java程序运行时,每个线程都会有一个对应的虚拟机栈。
栈帧是虚拟机栈中的一个元素,它用于存储一个方法的执行状态。在一个方法被执行时,虚拟机就会创建一个对应的栈帧,并将其压入虚拟机栈中。当这个方法执行完毕后,对应的栈帧也会从虚拟机栈中弹出,恢复到调用该方法的上一个方法的执行状态。
因此,栈和虚拟机栈都是数据结构,用于存储数据和指令等信息,但是前者通常是指物理内存中的一块区域,而后者则是Java虚拟机的一种抽象结构。而栈帧则是虚拟机栈中的一个元素,用于存储一个方法的执行状态。
4.总结
所以对于栈的这些习题我们就讲完了,下篇文章将会给大家讲解队列。在此,我们诚挚地邀请各位大佬们为我们点赞、关注,并在评论区留下您宝贵的意见与建议。让我们共同学习,共同进步,为知识的海洋增添更多宝贵的财富!🎉🎉🎉❤️❤️💕💕🥳👏👏👏