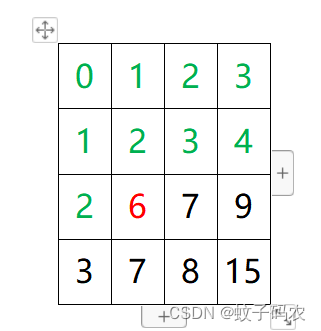
卷积的计算过程:各个神经元之间的线性组合并进行非线性变换
所谓深度卷积就是卷积之后再卷积,
更深的隐藏层来获取到更高级和更抽象的特征,以此来提高下游任务的精度。
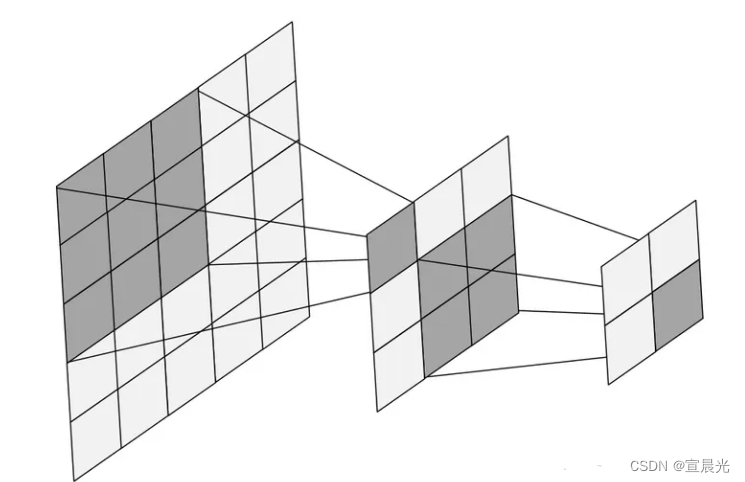
上图在input [5,5,1] 矩阵中,使用[3,3,1] 卷积核、步长为1 进行计算,得到[3,3,1]的feature map
可视野:
指经过卷积运算后特征图上的每个位置(元素)相对于原始特征输入的作用范围。
所以:
最右侧的特征图,针对中间的输入可视野是2x2,针对最左侧的可视野是4x4
中间的特征图,针对最左侧可视野是3x3
1、单通道单卷积核
输入 [5,5,1] 的单通道 灰度图,卷积核[3,3,1] ,偏置为1
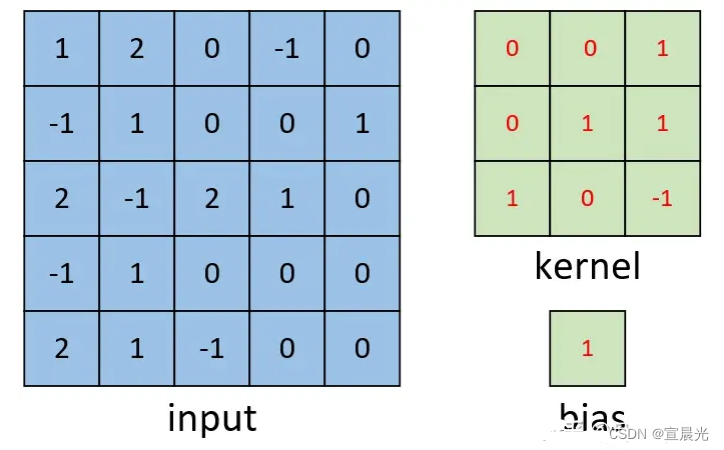
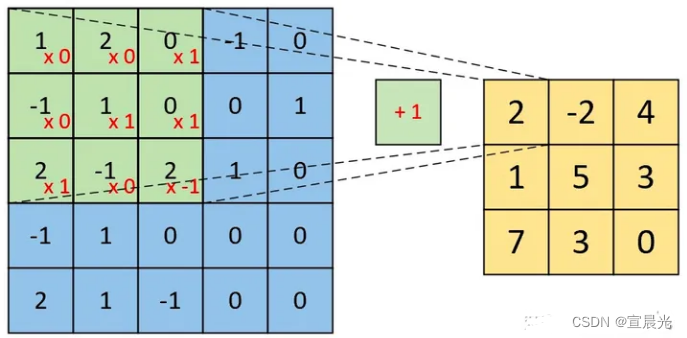
计算过程

2、单通道多卷积核
计算过程与单卷积核基本一致,得到[3,3,2] feature map。
最终结果是通道增加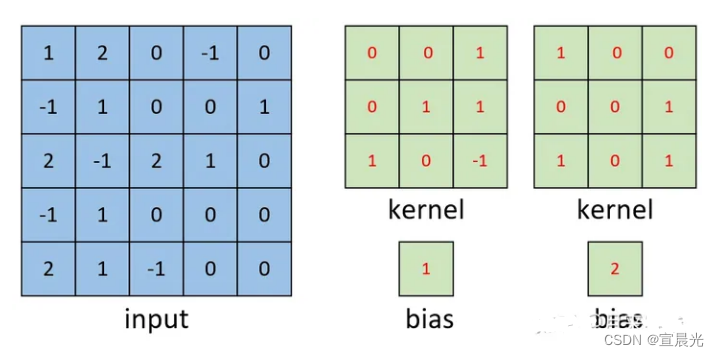
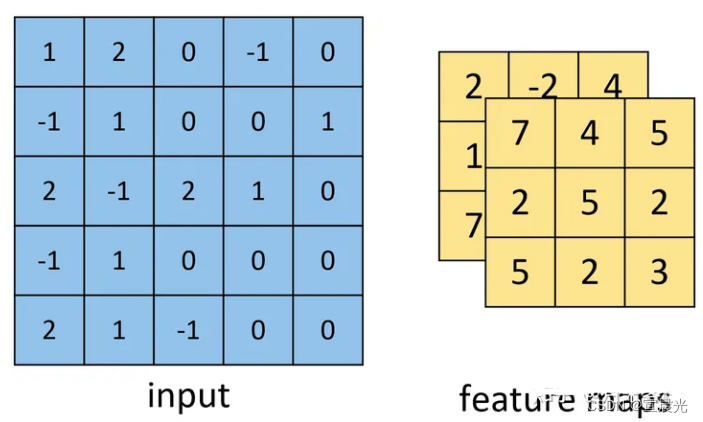
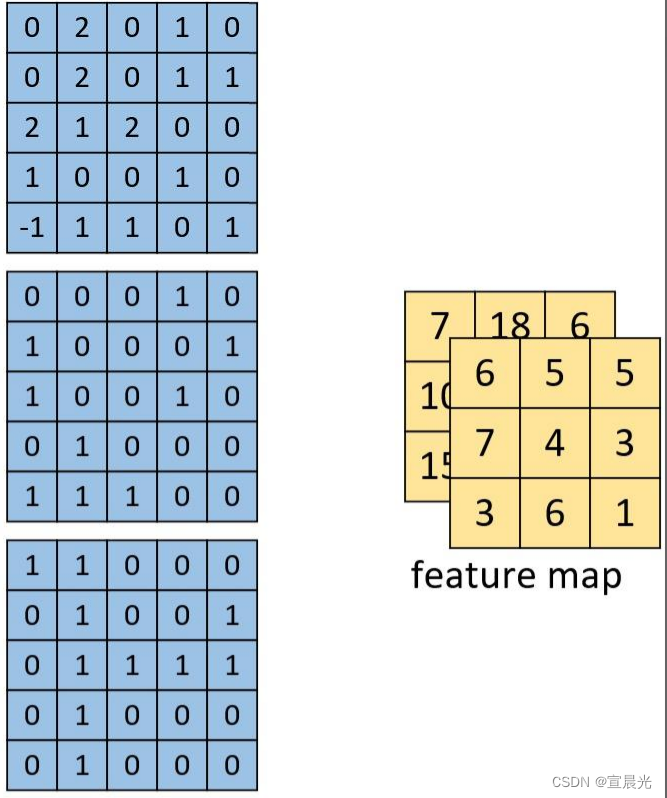
3、多通道单卷积核
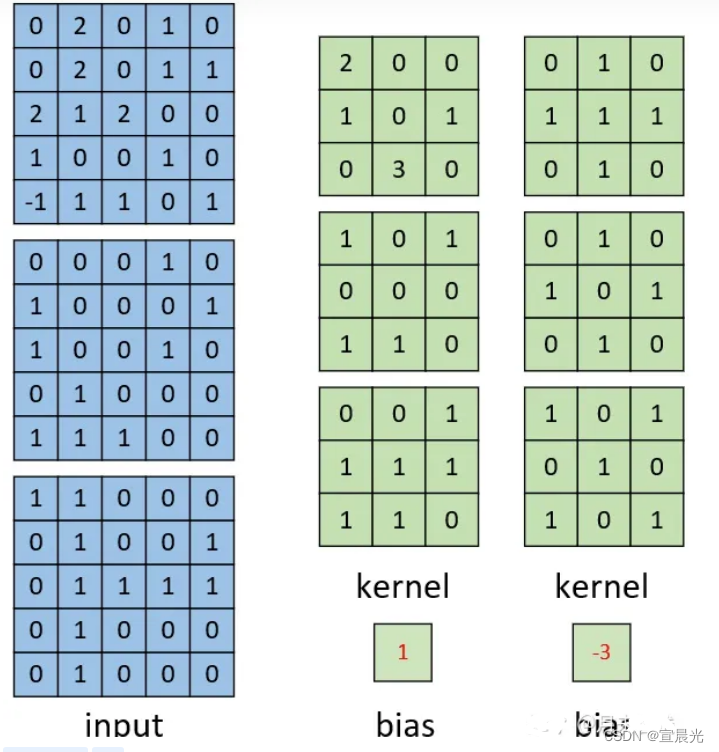
输入 【5,5,3】,卷积核【3,3,3】,偏置为1
右侧的卷积核是一个三通道,而不是三个卷积核,所以在进行卷积的时候对应的每一个卷积核都必须要有三个通道才能进行卷积
结果 【3,3,1】,单卷积核的卷积结果都是 1个通道

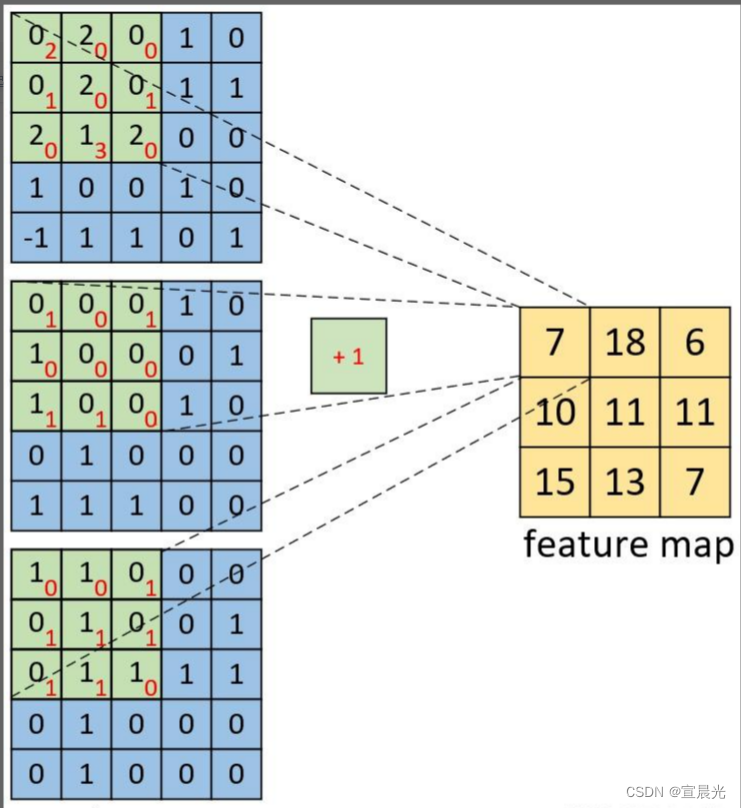
计算过程

4、多通道多卷积核
(1)原始输入有多少个通道,其对应的一个卷积核就必须要有多少个通道,这样才能与输入通道数匹配并完成卷积操作。换句话说,如果输入数据的形状为[n,n,c],那么对应每个卷积核的通道数也必须为c。
(2)用k个卷积核对输入进行卷积处理,那么最后得到的特征图一定就会包含有k个通道。例如,输入形状为[n,n,c],且用k个卷积核对其进行卷积,则卷积核的形状必定为[w1,w2,c,k],最终得到的特征图形状必定为[h1,h2,k];其中w1,w2为卷积核的宽度,h1,h2为卷积后特征图的宽度。
原文参考