本题可以说是运用二分查找的典例，即使是面对矩阵，只要是它保持“排序好”这样的结构，就一定能采用二分查找法。【你知道的，对于排序好的数组，二分查找几乎是最优秀的算法】

        当然，答案提供的是“Z字形查找法”【这个概念我搜不到，不过其实质，就是矩阵边界的缩减】

        “Z字形”排查效率高于二分查找法，只是因为题目结构特殊，一般不会有这种结构。

题目描述：

        编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例 1：

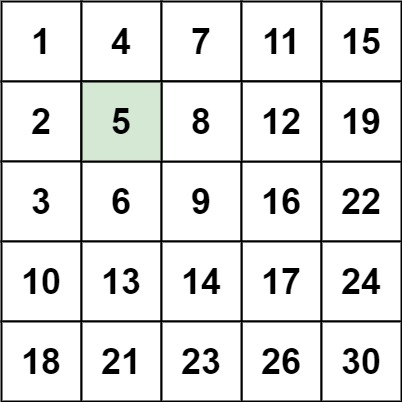
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -10^9 <= matrix[i][j] <= 10^9
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -10^9 <= target <= 10^9

解题准备：

        1.理解题意：本题的结构，非常特殊，对于matrix中的任一元素【i，j】，其具备四个属性，上、左的元素小于它，下、右的元素大于它【对于边界元素不讨论，类似】

        2.理解可能具备的操作：就此，大概率只需要查找一种操作即可。

        3.朴素的思路：对于矩阵，最简单的遍历原则就是，暴力遍历【从0行到len-1行，从0列到len2-1列，依次遍历元素】

        代码为：

for(int i=0; i<m; i++){for(int j=0; j<n; j++){// m是行数，n是列数。// 在这个语句段里操作}
}

        不过，虽然这样做，一定能找到target（或者发现根本没有），却浪费了约束条件：每一行、列存在递增的关系。

解题难点1分析：

        如果不从二分查找的角度，对于这种结构比较容易想到的优化方法为：

        1.遍历第0行的元素，依次判断大小（如果< target，+1），如果等于target直接返回true，如果大于target说明这一行不可能存在target，遍历下一行。

        2.接着上述，遍历第1行，同理……

        问题：时间复杂度仍高

                对于这种优化方案，如果是下图的结构：

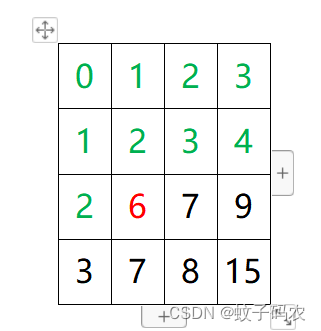
                容易发现，其遍历次数与暴力for一样多，所以时间复杂度的优化很差。

                就算是一般的结构，如果target比较大，很大概率前面k行，也得全部遍历（k随机），也就是说，时间复杂度没怎么优化。从最差优化的角度分析，时间复杂度仍是O（m*n）；

        没办法，这种优化不可取，得从别的角度出发。

解题难点2分析：

        从二分查找的角度出发，既然行列间满足递增的约束，那么对于每一行，必然也满足递增的约束。

        拆分每一行，拆成0到len-1行，每一行用二分查找查找，时间复杂度为O（logN）。

        由于遍历0到len-1行，所以总的时间复杂度是O（m * log n）；

        代码在此不写了，比较简单。

        不过，这道题是个强约束，拆分后，反而增加了查找时间复杂度。

解题难点3分析：

        从结构本身出发，由于行列间递增，那么，应该能处理特殊的数据。

        什么意思呢？我们用【0，0】，【0，len-1】，【len2-1，0】，【len-1，len2-1】维护矩阵的四个角的数据。

        由于矩阵的特殊性质，我们知道：【0，0】一定是最小的，【0，len-1】一定是0行最大的，【len2-1，0】一定是0列最大的，【len-1， len2-1】一定是所有数据最大的。

        如果矩阵中存在target，那么它一定大于【0，0】，小于【len-1，len2-1】。

        如果target大于【0， len-1】呢？这说明，target大于0行所有元素，那需要继续查找0行吗？

        可以直接忽略，从第1行开始查找。

        不过，target可能小于【0， len-1】，同时大于【0， 0】，这说明它可能在第0行。

        这时候从【len2-1， 0】开始判断，问题又来了：可能target同时大于【0，0】，小于【len2-1，0】

        不过，如果target小于【len2-1， 0】，不就说明：第len2-1行，都比target大吗？（因为【len2-1，0】在该行最小）

        那么，往上移动一行，不就行了？        

        其实从这个角度，看【0， len-1】也一样，如果target小于【0，len-1】，不就说明target小于len-1列的所有元素吗？

        往回退一列，不就行了？

        为了保持一致性，建议在四个角中，拿一个元素操作即可。

        该算法，每次可以排除一行或者一列，效率更高一些。

以上内容即我想分享的关于力扣热题18的一些知识。

        我是蚊子码农，如有补充，欢迎在评论区留言。个人也是初学者，知识体系可能没有那么完善，希望各位多多指正，谢谢大家。