蓝桥杯每日真题

蓝桥杯每日真题 - 第20天

devtools/2024/11/25 6:08:23/

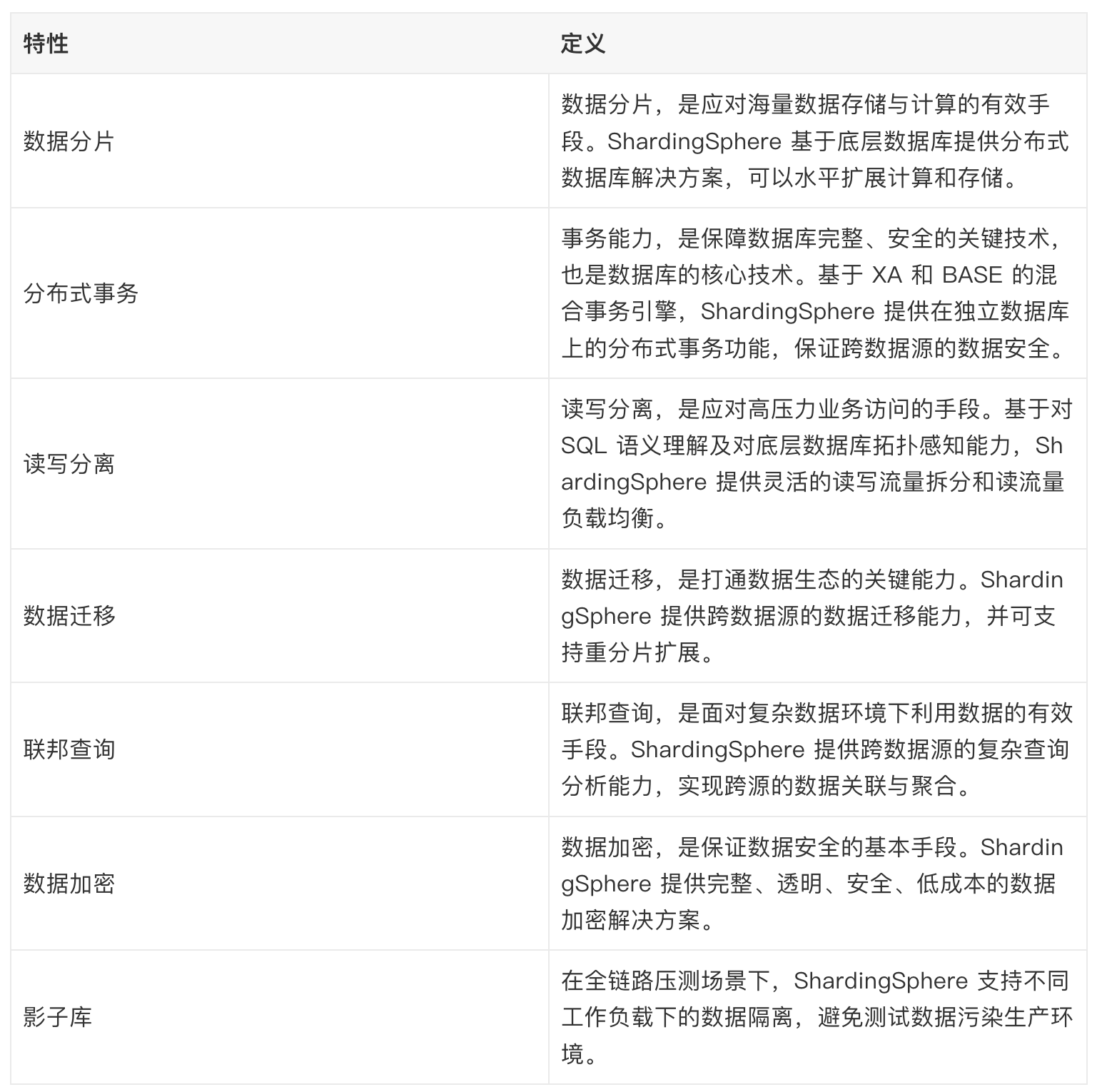
题目：（机房）

题目描述（13届 C&C+G题）

解题思路：

这道题目可以看作在一个无向图中查找两点之间的最短路径。题目中的 n 台电脑和 n−1 根网线形成了一棵树，树是一个特殊的无向图，因此我们可以利用 广度优先搜索（BFS） 来求解最短路径问题。

建图：
- 通过输入的 n−1 对电脑连接关系构建邻接表表示的无向图。
最短路径搜索：
- 利用 BFS，从起点开始逐层扩展，找到终点时输出步数。
- 由于树的性质，BFS的第一条找到的路径一定是最短路径。
多个查询的处理：
- 每次查询直接用 BFS 求解从起点到终点的最短路径。

代码实现（C语言）：

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int road(int start,int end,int dex,int num,int bef,int n);
int map[10000][10000];
int dey[10000];
int main()
{    int n,m;scanf("%d",&n);scanf("%d",&m);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){if(i==j){map[i][j]=1;}else{map[i][j]=0;}}dey[i]=-1;}for(int i=1;i<=n-1;i++){int a;int b;scanf("%d",&a);scanf("%d",&b);map[a][b]=1;map[b][a]=1;}int q[m+1][2];for(int i=1;i<=m;i++){scanf("%d",&q[i][0]);scanf("%d",&q[i][1]);}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dey[i]=dey[i]+map[i][j];}}for(int i=1;i<=m;i++){printf("%d\n",road(q[i][0],q[i][1],q[i][0],0,-1,n));}return 0;
}int road(int start,int end,int dex,int num,int bef,int n)
{//printf("%d to %d have %d\n",bef,dex,num);if(dex==end){return num+dey[dex];}else{int new_num=num+dey[dex];int lin=-100;int e=0;for(int i=1;i<=n;i++){if(i!=dex && map[i][dex]==1 && i!=bef){lin=fmax(lin,road(start,end,i,new_num,dex,n));e=e+1;}}if(e==0){return -100;}else{return lin;}}
}

得到运行结果：

代码分析：

初始化部分
- 通过输入节点数n和边数m，创建一个邻接矩阵来表示图，初始化每个节点的度数为-1。
- 将图的边输入，并更新邻接矩阵。
查询输入部分
- 输入多个查询，每个查询要求计算从一个节点到另一个节点的路径代价。
计算每个节点的度数
- 遍历邻接矩阵，计算每个节点的度数，并将其存储在一个数组中。
计算路径代价的递归函数
- 使用深度优先搜索（DFS）递归遍历路径，如果当前节点是终点，则返回路径代价；否则，继续递归遍历与当前节点相邻的未访问节点。
- 每到一个节点，路径代价会累加该节点的度数。
输出查询结果
- 对每个查询，调用递归函数计算路径代价，并输出结果。