目录
一、K-means和DBSCAN之间的主要区别
二、DBSCAN聚类算法
2.1DBSCAN聚类算法实现点集数据的聚类
2.2DBSCAN聚类算法实现鸢尾花数据集的聚类
三、K-means聚类算法
3.1K-means聚类算法实现随机数据的聚类
3.2K-means聚类算法实现鸢尾花数据集的聚类
一、K-means和DBSCAN之间的主要区别
1.聚类原理:
K-means:K-means是一种基于距离的聚类算法,它将数据点划分为K个簇,通过最小化数据点与所属簇的质心之间的平方距离来确定聚类结果。K-means假设聚类簇为凸形,并且簇的大小差异较小。
DBSCAN:DBSCAN是一种基于密度的聚类算法,它通过确定数据点的密度来划分聚类。DBSCAN将高密度区域视为聚类,并能够识别出噪声点和孤立点。相比于K-means,DBSCAN对聚类簇的形状没有预设要求,可以发现任意形状的聚类簇。
2.聚类数量:
K-means:K-means需要预先指定聚类的数量K。这是因为K-means是一个划分式聚类方法,需要事先确定聚类簇的数量,然后将数据点划分为K个簇。
DBSCAN:DBSCAN不需要预先指定聚类的数量。它根据数据点的密度来决定聚类的形状和数量,可以自动发现不同大小和形状的聚类簇。
3.处理噪声和孤立点:
K-means:K-means对噪声和孤立点敏感。它会将这些数据点分配到离它们最近的聚类簇中,即使这些数据点在实际中并不属于任何簇。
DBSCAN:DBSCAN能够有效地处理噪声和孤立点。它将这些数据点标记为噪声或边界点,不归属于任何聚类簇。
4.参数选择:
K-means:K-means需要事先指定聚类的数量K,这需要一定的先验知识或通过试验和评估来确定最佳的K值。
DBSCAN:DBSCAN需要调整两个关键参数:领域半径(eps)和最小样本数(min_samples)。这些参数的选择可以影响聚类结果,需要根据数据集的特点进行调优。
二、DBSCAN聚类算法
2.1DBSCAN聚类算法实现点集数据的聚类
代码:
from sklearn import datasets
import numpy as np
import random
import matplotlib.pyplot as plt
import time
import copydef find_neighbor(j, x, eps):N = list()for i in range(x.shape[0]):temp = np.sqrt(np.sum(np.square(x[j] - x[i]))) # 计算欧式距离if temp <= eps:N.append(i)return set(N)def DBSCAN(X, eps, min_Pts):k = -1neighbor_list = [] # 用来保存每个数据的邻域omega_list = [] # 核心对象集合gama = set([x for x in range(len(X))]) # 初始时将所有点标记为未访问cluster = [-1 for _ in range(len(X))] # 聚类for i in range(len(X)):neighbor_list.append(find_neighbor(i, X, eps))if len(neighbor_list[-1]) >= min_Pts:omega_list.append(i) # 将样本加入核心对象集合omega_list = set(omega_list) # 转化为集合便于操作while len(omega_list) > 0:gama_old = copy.deepcopy(gama)j = random.choice(list(omega_list)) # 随机选取一个核心对象k = k + 1Q = list()Q.append(j)gama.remove(j)while len(Q) > 0:q = Q[0]Q.remove(q)if len(neighbor_list[q]) >= min_Pts:delta = neighbor_list[q] & gamadeltalist = list(delta)for i in range(len(delta)):Q.append(deltalist[i])gama = gama - deltaCk = gama_old - gamaCklist = list(Ck)for i in range(len(Ck)):cluster[Cklist[i]] = komega_list = omega_list - Ckreturn clusterX1, y1 = datasets.make_circles(n_samples=2000, factor=.6, noise=.02)
X2, y2 = datasets.make_blobs(n_samples=400, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[.1]], random_state=9)
X = np.concatenate((X1, X2))
eps = 0.08
min_Pts = 10
begin = time.time()
C = DBSCAN(X, eps, min_Pts)
end = time.time()
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=C)
plt.show()结果:

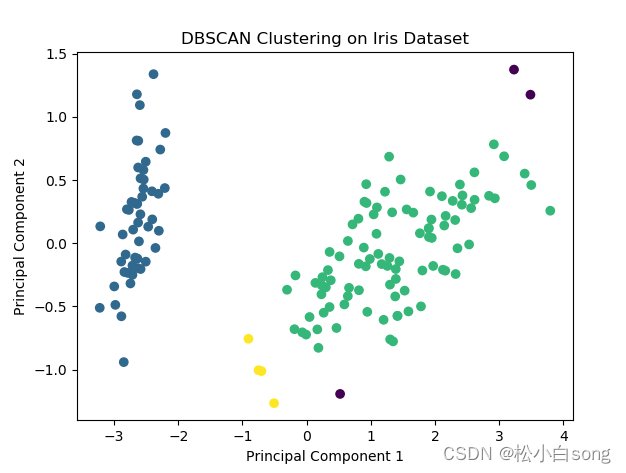
2.2DBSCAN聚类算法实现鸢尾花数据集的聚类
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA# 加载鸢尾花数据集
iris = load_iris()
X = iris.data# 使用PCA进行数据降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)# 使用DBSCAN进行聚类
dbscan = DBSCAN(eps=0.4, min_samples=3)
labels = dbscan.fit_predict(X_pca)# 绘制聚类结果
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=labels)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('DBSCAN Clustering on Iris Dataset')
plt.show()结果:
三、K-means聚类算法
3.1K-means聚类算法实现随机数据的聚类
代码:
import torch
import math
import matplotlib.pyplot as pltdef dis(a, b):return math.sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]))X = torch.randn(2000) * 100
y = torch.randn(2000) * 100
C = torch.zeros(2000)K = 5
CentPoint = []for i in range(K):CentPoint.append([torch.randint(-100, 100, (1,)).item(),torch.randint(-100, 100, (1,)).item()])print(CentPoint)
for p in range(10):NewPoint = [[0, 0] for i in range(K)]for i in range(len(X)):mDis = 1e9mC = 0for j in range(len(CentPoint)):cp = CentPoint[j]D = dis([X[i].item(), y[i].item()], cp)if mDis > D:mDis = DmC = jC[i] = mCNewPoint[mC][0] += X[i].item()NewPoint[mC][1] += y[i].item()for i in range(K):CentPoint[i][0] = NewPoint[i][0] / 2000CentPoint[i][1] = NewPoint[i][1] / 2000print(CentPoint)cc = list(C)
for i in range(len(X)):if cc[i] == 0:plt.plot(X[i].item(), y[i].item(), 'r.')elif cc[i] == 1:plt.plot(X[i].item(), y[i].item(), 'g.')elif cc[i] == 2:plt.plot(X[i].item(), y[i].item(), 'b.')elif cc[i] == 3:plt.plot(X[i].item(), y[i].item(), color='pink', marker='.')elif cc[i] == 4:plt.plot(X[i].item(), y[i].item(), color='orange', marker='.')for CP in CentPoint:plt.plot(CP[0], CP[1], color='black', marker='X')plt.show()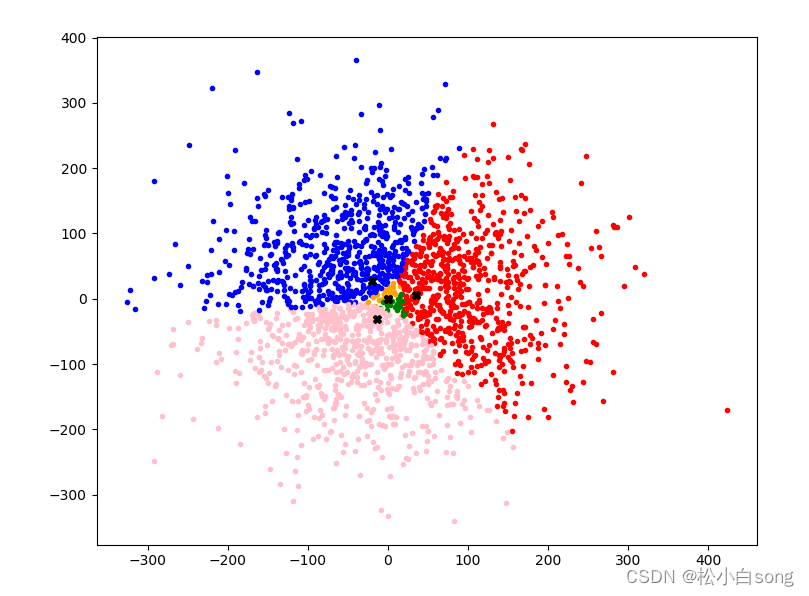
3.2K-means聚类算法实现鸢尾花数据集的聚类
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA# 加载鸢尾花数据集
iris = load_iris()
X = iris.data# 使用PCA进行数据降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)# 使用K-means进行聚类
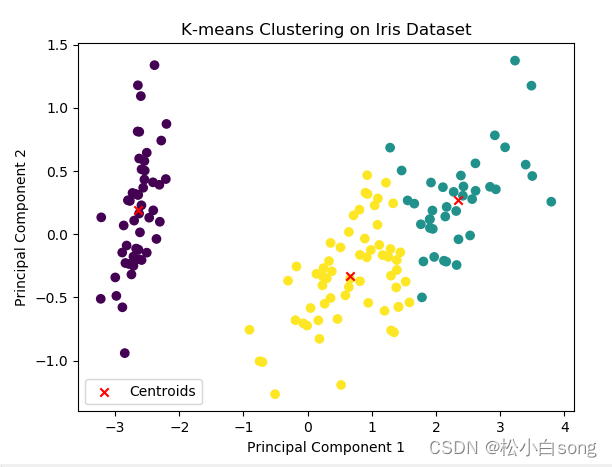
kmeans = KMeans(n_clusters=3, random_state=0)
labels = kmeans.fit_predict(X_pca)# 绘制聚类结果
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=labels)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], marker='x', color='red', label='Centroids')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('K-means Clustering on Iris Dataset')
plt.legend()
plt.show()结果: