目录
前言
树
树的定义
树的相关概念
树的遍历
1 先序遍历
2 中序遍历
3 后序遍历
前言
前两篇文章(【C++算法竞赛 · 图论】图论基础、【C++算法竞赛 · 图论】图的存储)中,介绍了图的相关概念与存储,还不了解的可以去补补课。
这篇文章会介绍一种 特殊的图的形式:树 。话不多说,步入正题——
树
树的定义
顾名思义,树是一种长得很像现实中的树的图,只是它是倒过来的。请看此图:
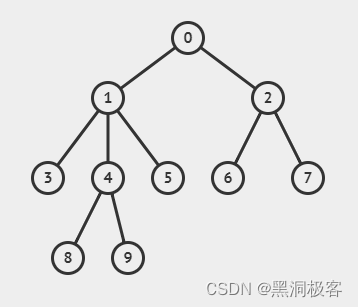
这就是一棵十分普通的树。
树的相关概念
- 每一个数称为 节点 (node) 。
- 作为所有其他节点的“起源”的节点称为 根节点(root),也就是图中的 0。
- 如果 u 是 v 的上一个节点(例如 1 和 4),那么 u 是 v 的 父节点(parent node),v 是 u 的 子节点(child node)。
- 没有子节点的节点,也就是树的末端,称作 叶节点。
- 以某个节点为根节点的树被称作原来的树的 子树(subtree)。
- 多棵树的集合被称为 森林(forest)。
树的遍历
按照某种次序来访问树中全部节点,这种操作叫做 树的遍历。
树的遍历一般有三种方式:(BFS,DFS在之后的文章中讲哦)
1 先序遍历
先访问根节点,然后按照从左到右的顺序遍历各子树。
此图的先序遍历为:0 1 3 4 8 9 5 2 6 7
2 中序遍历
先访问左子树,然后访问根,最后访问右子树。
注意:这种方法仅限于二叉树!
此图的中序遍历为:6 1 7 5 8 0 3 2 9 4
3 后序遍历
先从左到右访问子树,然后访问根节点。
此图的后序遍历为:3 8 9 4 5 1 6 7 2 0
这期内容不长(学生党作业多),主要是树的基础概念,之后会继续讲二叉树、BFS、DFS等内容,别急!
本篇文章就到这啦,别忘点赞收藏(求求了!)
下次见!