目录
编辑
一、基本概念
二、哈夫曼树的构造算法
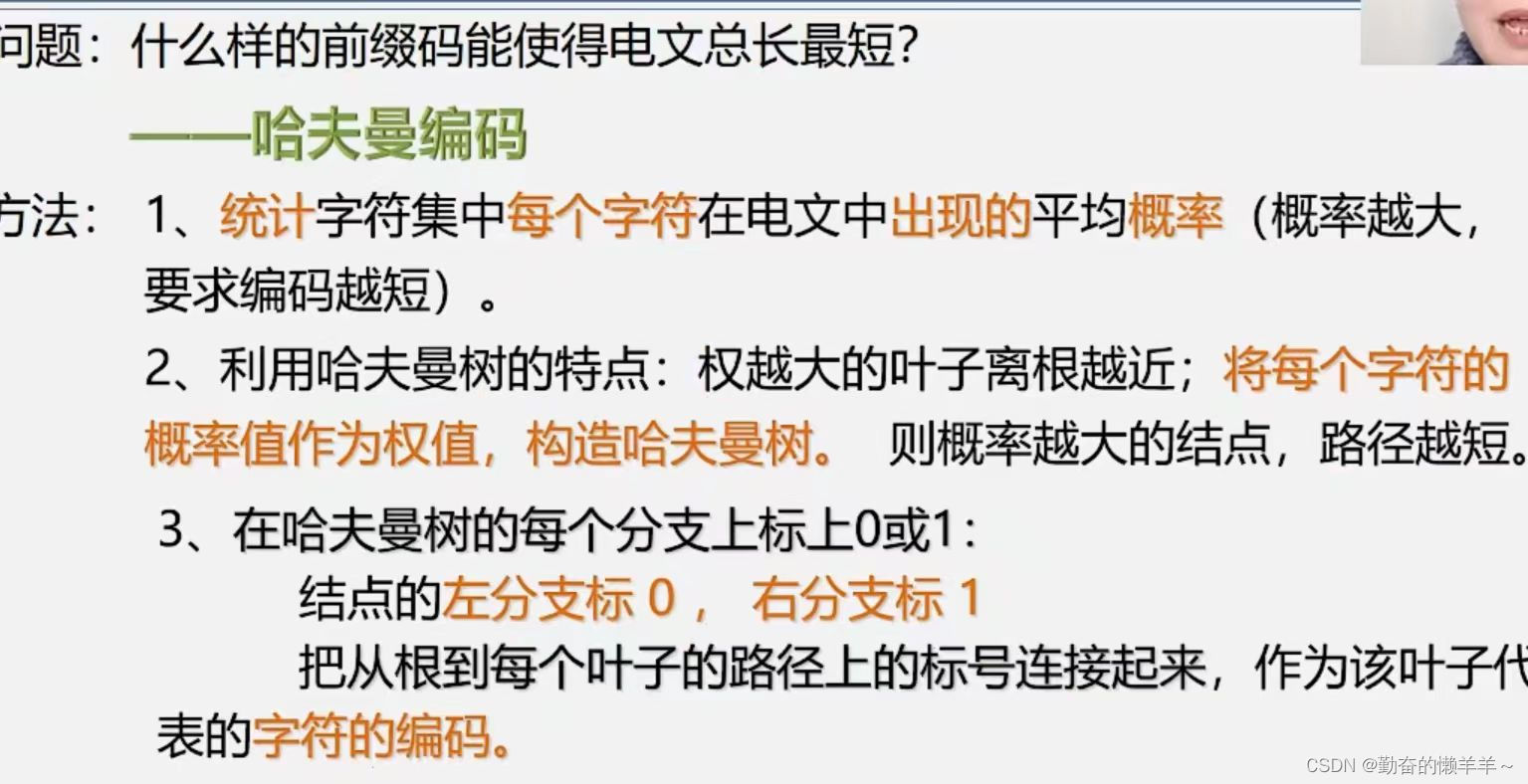
三、哈夫曼编码
假如<60分的同学占5%,60到70分的占15%……
这里的百分数就是权。
此时,效率最高(判断次数最少)的树就是哈夫曼树。
一、基本概念
权(weight):将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度:从根结点到该结点之间的路径长度与该结点的权的乘积。
树的路径长度:从树根到每一个结点的路径长度之和。记作TL
结点的带权路径长度:从根节点到该结点之间的路径长度与该结点的权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
哈夫曼树:最优树(带权路径长度最短的树)
注:“带权路径最短”是在度相同的树中比较而得到的。
哈夫曼树:最优二叉树(带权路径长度最短的二叉树)
哈夫曼树中权越大的叶子离跟越近
二、哈夫曼树的构造算法


哈夫曼树构造算法的实现:
采用顺序存储结构:一维结构数组 HuffmanTree H;
结点类型定义:
typedef struct {int weight;int parent, lch, rch; }HTNode,*HuffmanTree;1、初始化HT[1……2n-1]:lch=rch=parent=0;
2、输入初始n个叶子结点:置HT[1……n]的weight值;
3、进行以下n-1次合并,依次产生n-1个结点HT[i],i=n+1……2n-1;
a)在HT[1..i-1]中选两个未被选过(从parent==0的结点中选)的weight最小的两个结点HT[s1]和HT[s2],s1、s2为两个最小结点下标;
b)修改HT[s1]和HT[s2]的parent值:HT[s1].parent=i; HT[s2].parent=i;
Dc)修改新产生的HT[i]:
HT[i].weight=HT[s1].weight + HT[s2].weight;
HT[i].lch=s1;HT[i].rch=s2;