分类目录:《深入理解深度学习》总目录
当训练有足够的表示能力甚至会过拟合的大模型时,我们经常观察到,训练误差会随着时间的推移逐渐降低但验证集的误差会再次上升。下图是这些现象的一个例子,这种现象几乎一定会出现。
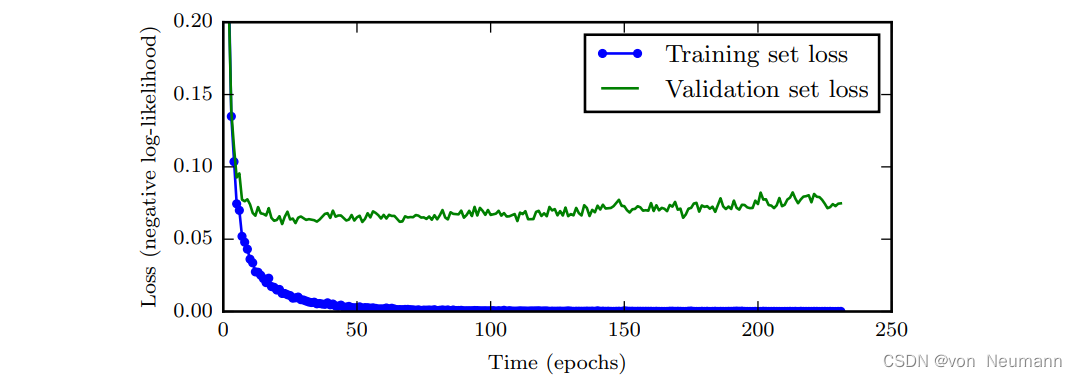
这意味着我们只要返回使验证集误差最低的参数设置,就可以获得验证集误差更低的模型(并且因此有希望获得更好的测试误差)。在每次验证集误差有所改善后,我们存储模型参数的副本。当训练算法终止时,我们返回这些参数而不是最新的参数。当验证集上的误差在事先指定的循环次数内没有进一步改善时,算法就会终止。这种策略被称为提前终止(Early Stopping)。这可能是深度学习中最常用的正则化形式。它的流行主要是因为有效性和简单性。
我们可以认为提前终止是非常高效的超参数选择算法。按照这种观点,训练步数仅是另一个超参数。我们从上图可以看到,这个超参数在验证集上具有U型性能曲线。很多控制模型容量的超参数在验证集上都是这样的U型性能曲线。在提前终止的情况下,我们通过控制拟合训练集的步数来控制模型的有效容量。大多数超参数的选择必须使用高代价的猜测和检查过程,我们需要在训练开始时猜测一个超参数,然后运行几个步骤检查它的训练效果。‘‘训练时间’’ 是唯一只要跑一次训练就能尝试很多值的超参数。通过提前终止自动选择超参数的唯一显著的代价是训练期间要定期评估验证集。在理想情况下,这可以并行在与主训练过程分离的机器上,或独立的CPU,或独立的GPU上完成。如果没有这些额外的资源,可以使用比训练集小的验证集或较不频繁地评估验证集来减小评估代价,较粗略地估算取得最佳的训练时间。
另一个提前终止的额外代价是需要保持最佳的参数副本。这种代价一般是可忽略的,因为可以将它储存在较慢较大的存储器上(例如,在GPU内存中训练,但将最佳参数存储在主存储器或磁盘驱动器上)。由于最佳参数的写入很少发生而且从不在训练过程中读取,这些偶发的慢写入对总训练时间的影响不大。
提前终止是一种非常不显眼的正则化形式,它几乎不需要改变基本训练过程、目标函数或一组允许的参数值。这意味着,无需破坏学习动态就能很容易地使用提前终止。相对于权重衰减,必须小心不能使用太多的权重衰减,以防网络陷入不良局部极小点(对应于病态的小权重)。提前终止可单独使用或与其他的正则化策略结合使用。即使为鼓励更好泛化,使用正则化策略改进目标函数,在训练目标的局部极小点达到最好泛化也是非常罕见的。
提前终止需要验证集,这意味着某些训练数据不能被馈送到模型。为了更好地利用这一额外的数据,我们可以在完成提前终止的首次训练之后,进行额外的训练。在第二轮,即额外的训练步骤中,所有的训练数据都被包括在内。有两个基本的策略都可以用于第二轮训练过程。一个策略是再次初始化模型,然后使用所有数据再次训练。在这个第二轮训练过程中,我们使用第一轮提前终止训练确定的最佳步数。此过程有一些细微之处。例如,我们没有办法知道重新训练时,对参数进行相同次数的更新和对数据集进行相同次数的遍历哪一个更好。由于训练集变大了,在第二轮训练时,每一次遍历数据集将会更多次地更新参数。另一个策略是保持从第一轮训练获得的参数,然后使用全部的数据继续训练。在这个阶段,已经没有验证集指导我们需要在训练多少步后终止。取而代之,我们可以监控验证集的平均损失函数,并继续训练,直到它低于提前终止过程终止时的目标值。此策略避免了重新训练模型的高成本,但表现并没有那么好。例如,验证集的目标不一定能达到之前的目标值,所以这种策略甚至不能保证终止。提前终止对减少训练过程的计算成本也是有用的。除了由于限制训练的迭代次数而明显减少的计算成本,还带来了正则化的益处(不需要添加惩罚项的代价函数或计算这种附加项的梯度)。
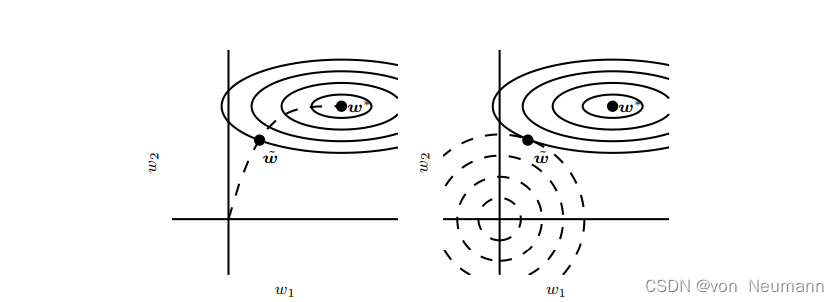
目前为止,我们已经声明提前终止是一种正则化策略,但我们只通过展示验证集误差的学习曲线是一个U型曲线来支持这种说法。我们认为提前终止可以将优化过程的参数空间限制在初始参数值 θ 0 \theta_0 θ0的小邻域内。更具体地,想象用学习率 ϵ \epsilon ϵ进行 τ \tau τ个优化步骤(对应于 τ \tau τ个训练迭代)。我们可以将 ϵ τ \epsilon\tau ϵτ作为有效容量的度量。假设梯度有界,限制迭代的次数和学习速率能够限制从 θ 0 \theta_0 θ0到达的参数空间的大小,如下图所示。在这个意义上, ϵ τ \epsilon\tau ϵτ的效果就好像是权重衰减系数的倒数。事实上,在二次误差的简单线性模型和简单的梯度下降情况下,我们可以展示提前终止相当于 L 2 L^2 L2正则化。
参考文献:
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015
[2] Aston Zhang, Zack C. Lipton, Mu Li, Alex J. Smola. Dive Into Deep Learning[J]. arXiv preprint arXiv:2106.11342, 2021.