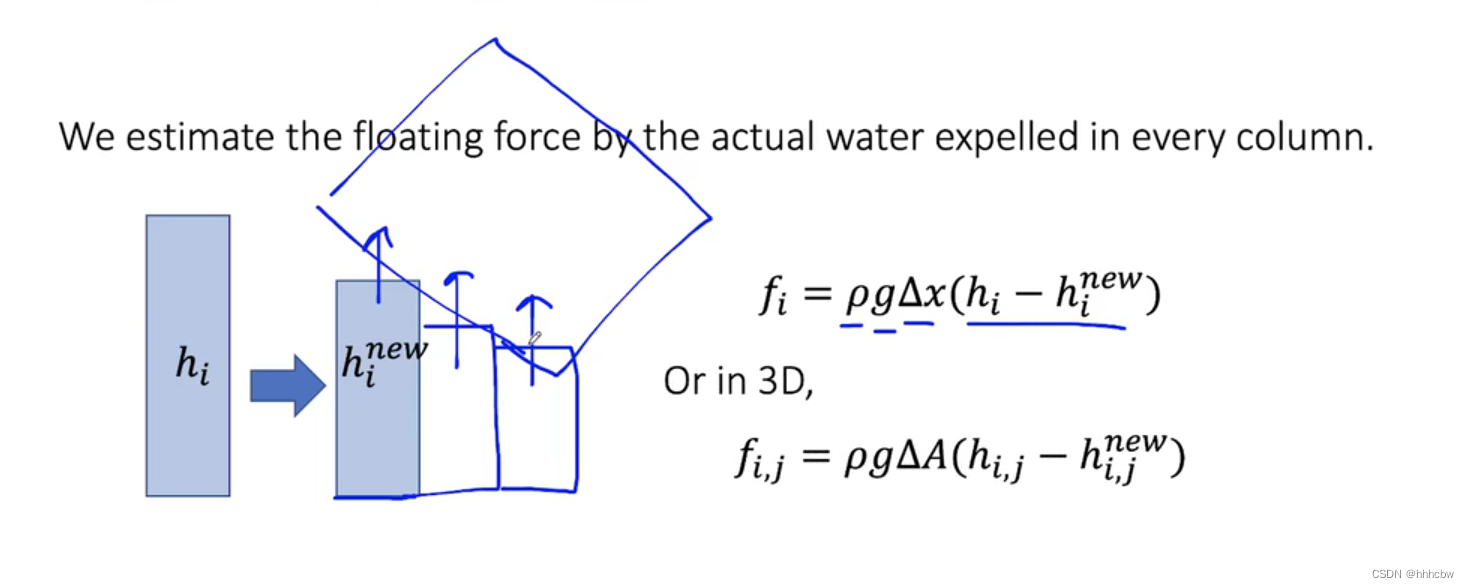实验四主要使用 Shallow Wave 模拟流体
完整项目已上传至github。
文章目录
- Height Feild(高度场)
- 更新高度场
- 更新速度场
- Shallow Wave Equation
- Discretization(离散化)
- 一阶导数
- 二阶导数
- Discretized Shallow Wave Equation
- Solution 1
- Solution 2
- Pressure(压强)
- Viscosity(粘滞)
- 算法
- 未考虑边界
- 考虑边界
- Two-Way Coupling
- 更新流体的高度场
- 算法
- 刚体更新
Height Feild(高度场)
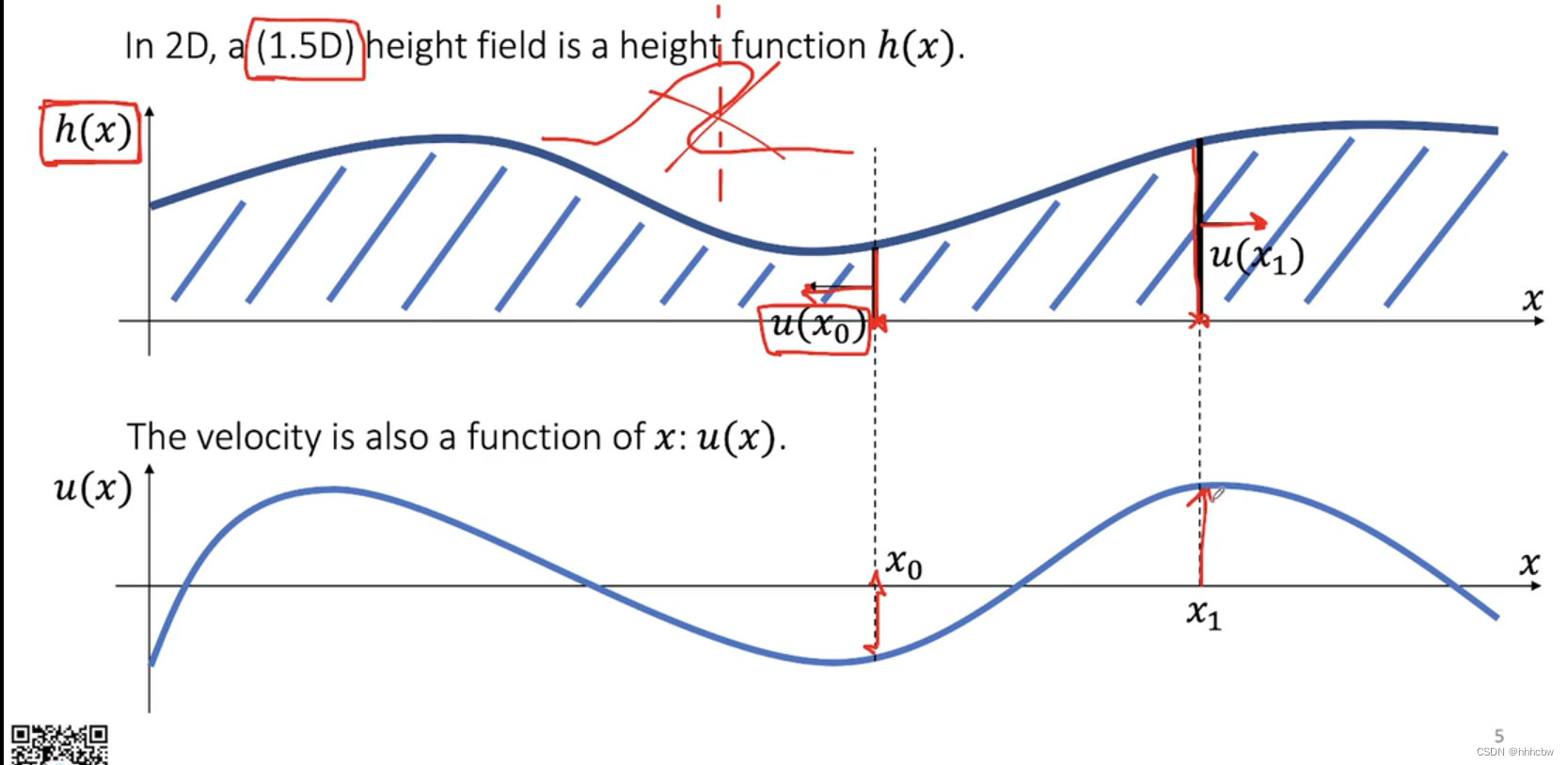
2D 中,高度场是一个高度函数 h ( x ) h(x) h(x),是 1.5D 的。3D 中,就是 2.5D 的。
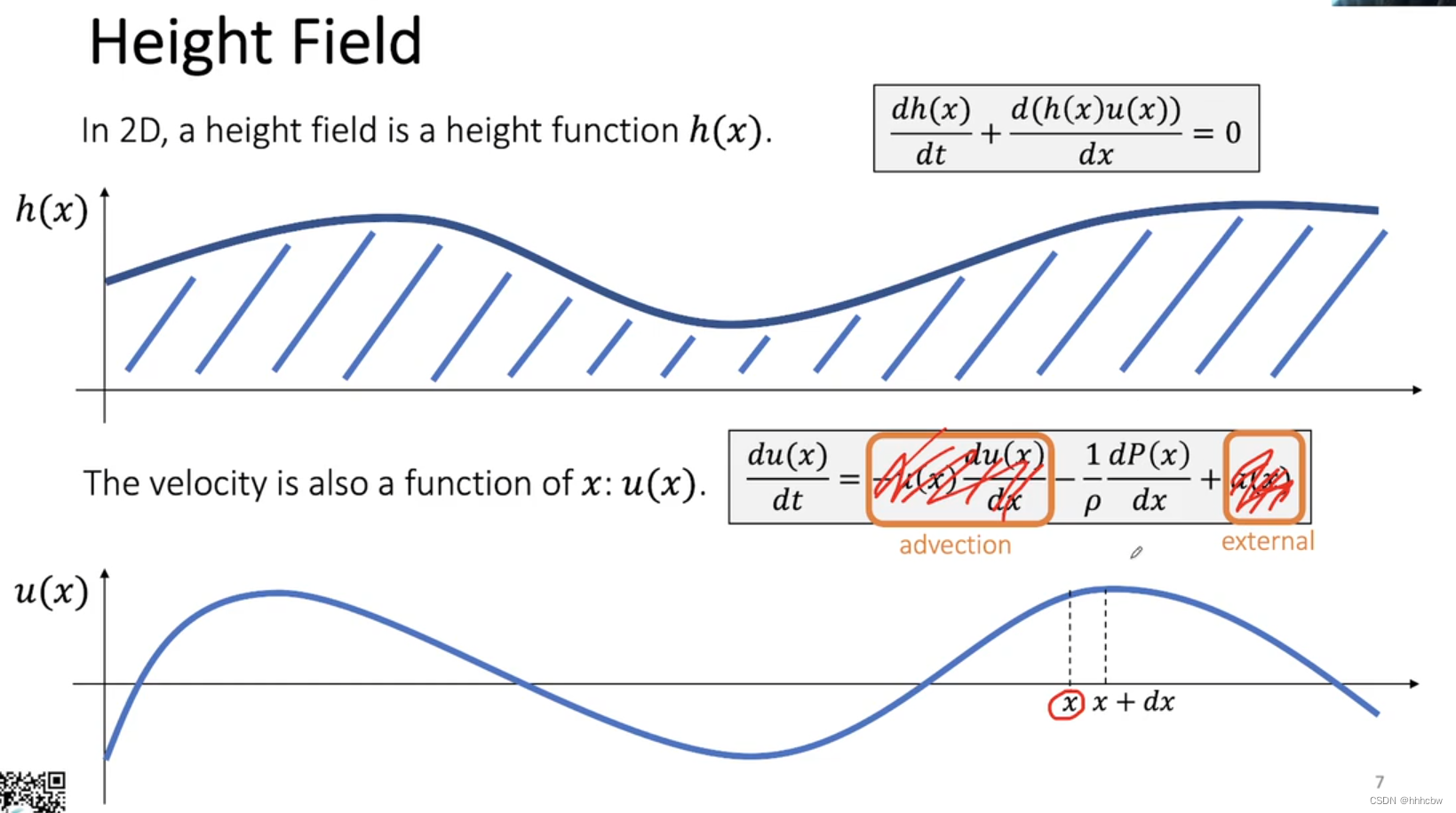
更新高度场
d h ( x ) d t \frac{dh(x)}{dt} dtdh(x) 表示 h ( x ) h(x) h(x) 随时间的变化; d ( h ( x ) u ( x ) ) = h ( x + d x ) u ( x + d x ) − h ( x ) u ( x ) d(h(x)u(x))=h(x+dx)u(x+dx)-h(x)u(x) d(h(x)u(x))=h(x+dx)u(x+dx)−h(x)u(x) 左边项是出来的水,右边项是进来的水,所以相减表示变化的水的量,再除以dx 就是高度的变化。

更新速度场
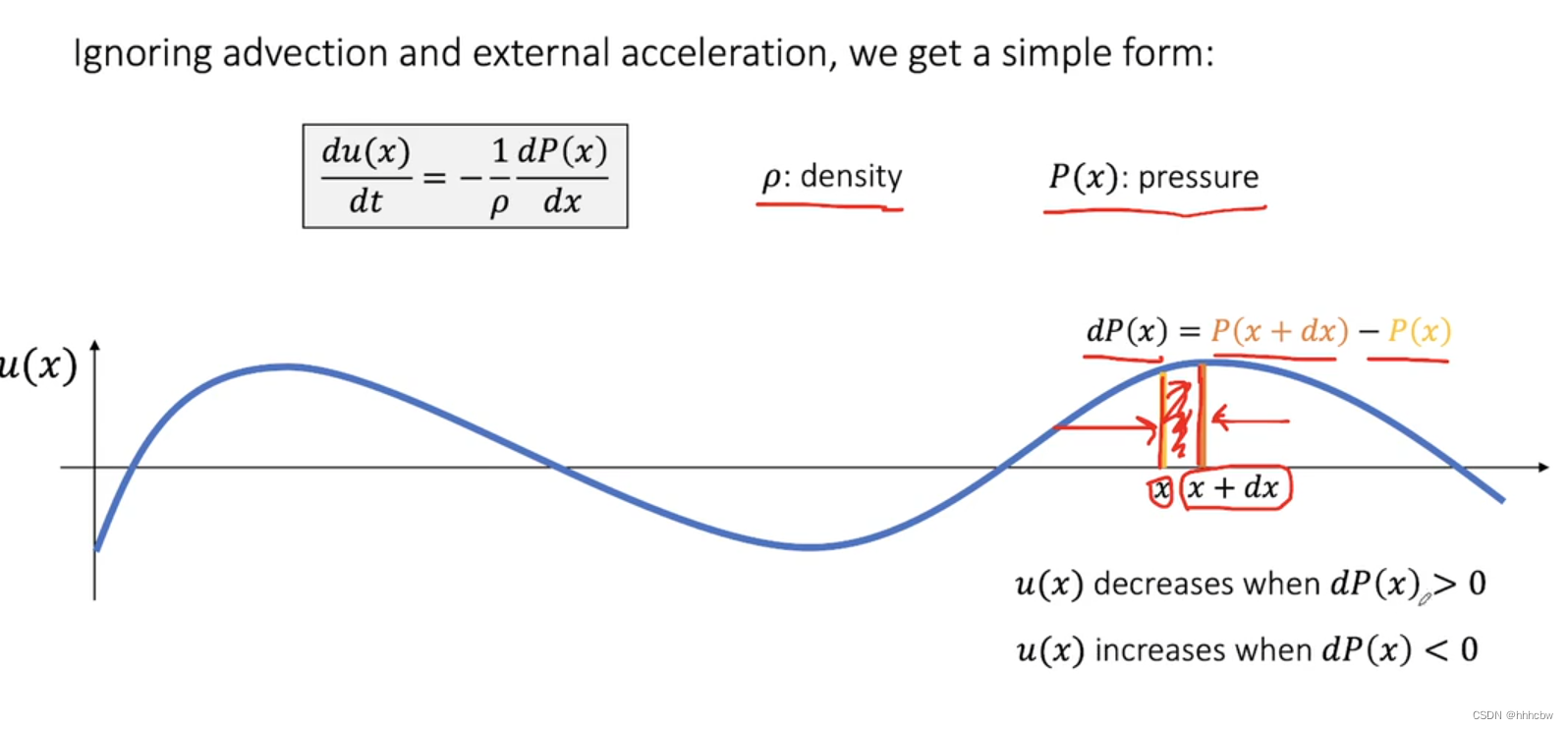
暂时忽略前后两项;速度场的更新与密度有关,密度越大越难推; d u ( x ) d t = a ( x ) = F m = P S ρ V = P ρ x \frac{du(x)}{dt}=a(x)=\frac{F}{m}=\frac{PS}{\rho V}=\frac{P}{\rho x} dtdu(x)=a(x)=mF=ρVPS=ρxP, 这里的 P = − d P ( x ) P = - dP(x) P=−dP(x) 因为这里是压强差
d P ( x ) > 0 dP(x)>0 dP(x)>0 表示右边的压强大于左边,所以速度会变小(与正方向相反,这里不是大小)。 d P ( x ) < 0 dP(x) < 0 dP(x)<0 则是右边的压强小于左边,所以速度会变大(与正方向相同)
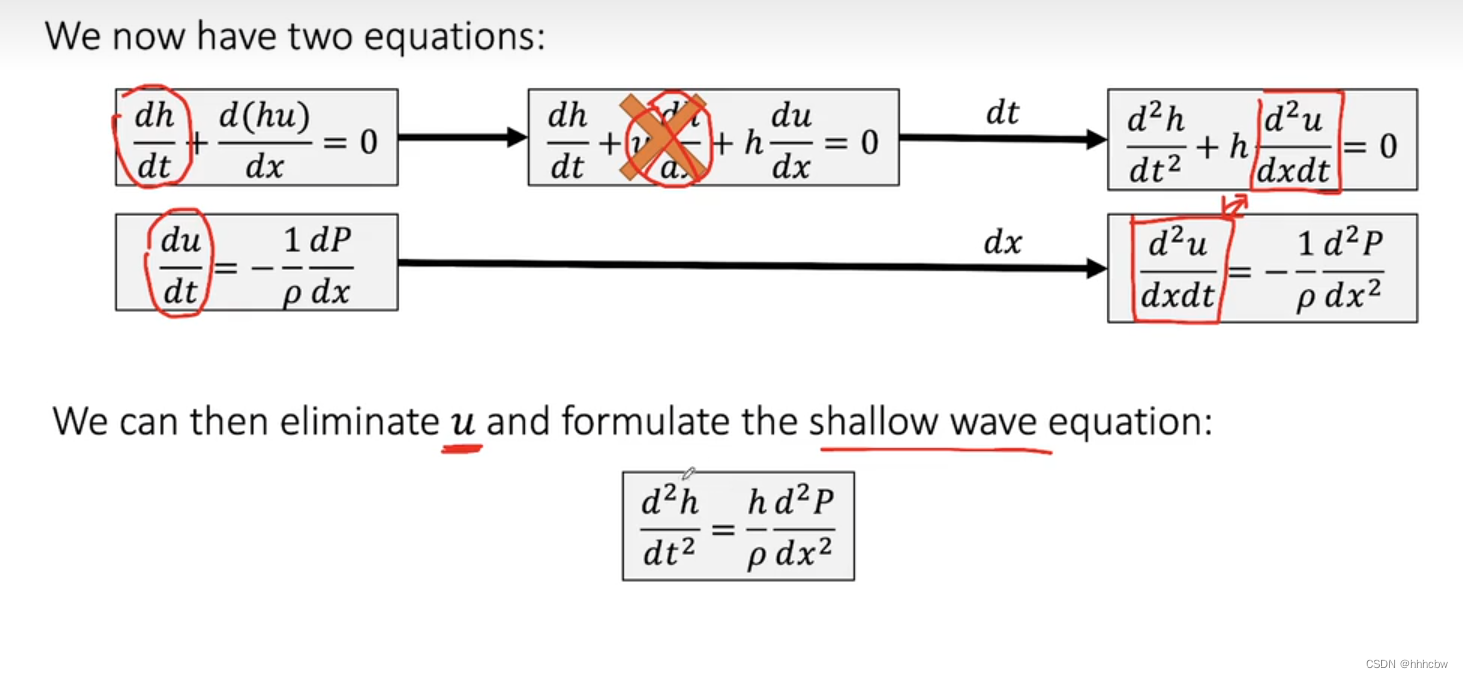
Shallow Wave Equation
Shallow Wave 方法就是通过忽略 u d u d x u\frac{du}{dx} udxdu 达到只考虑高度场的目的。
Discretization(离散化)
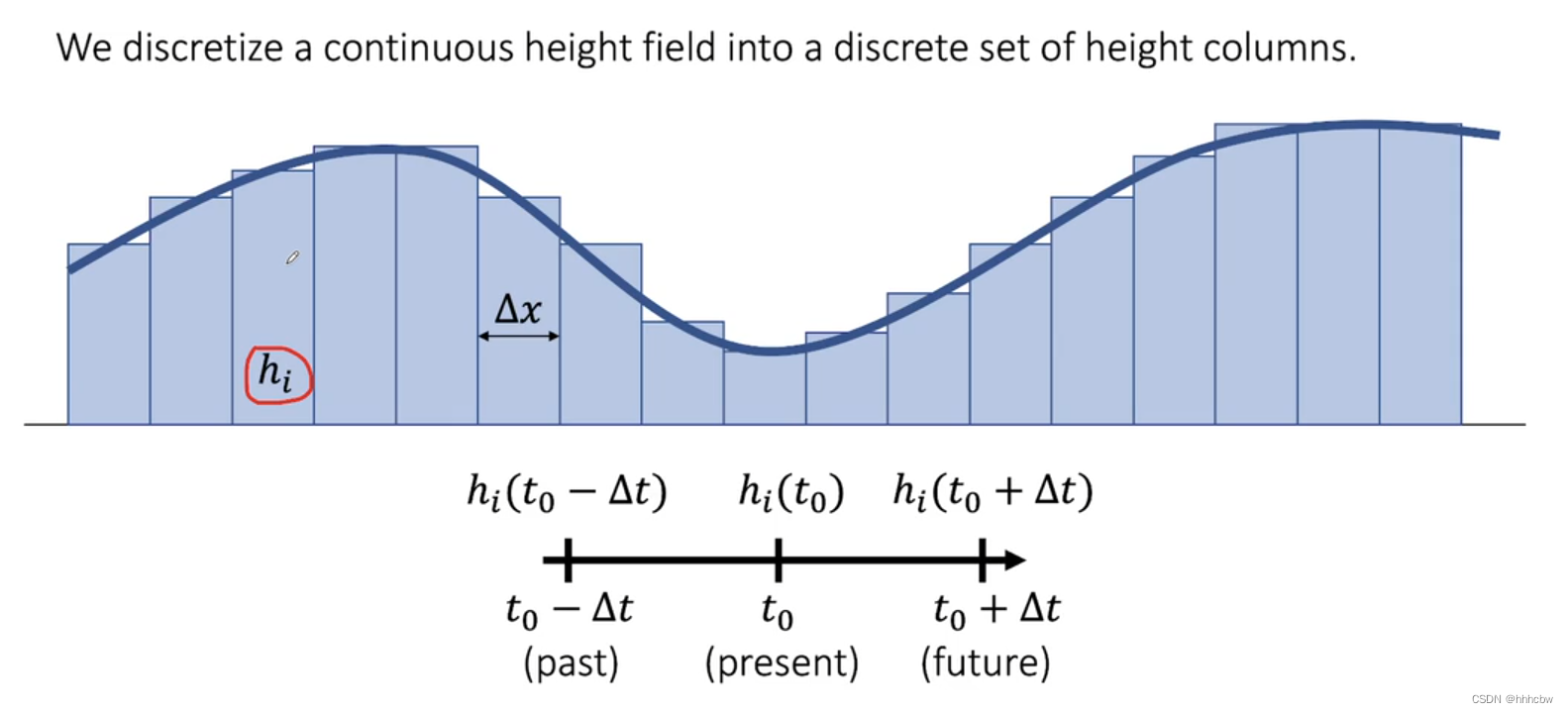
当然,我们不能直接处理连续的函数,因此需要将高度场离散化。
一阶导数
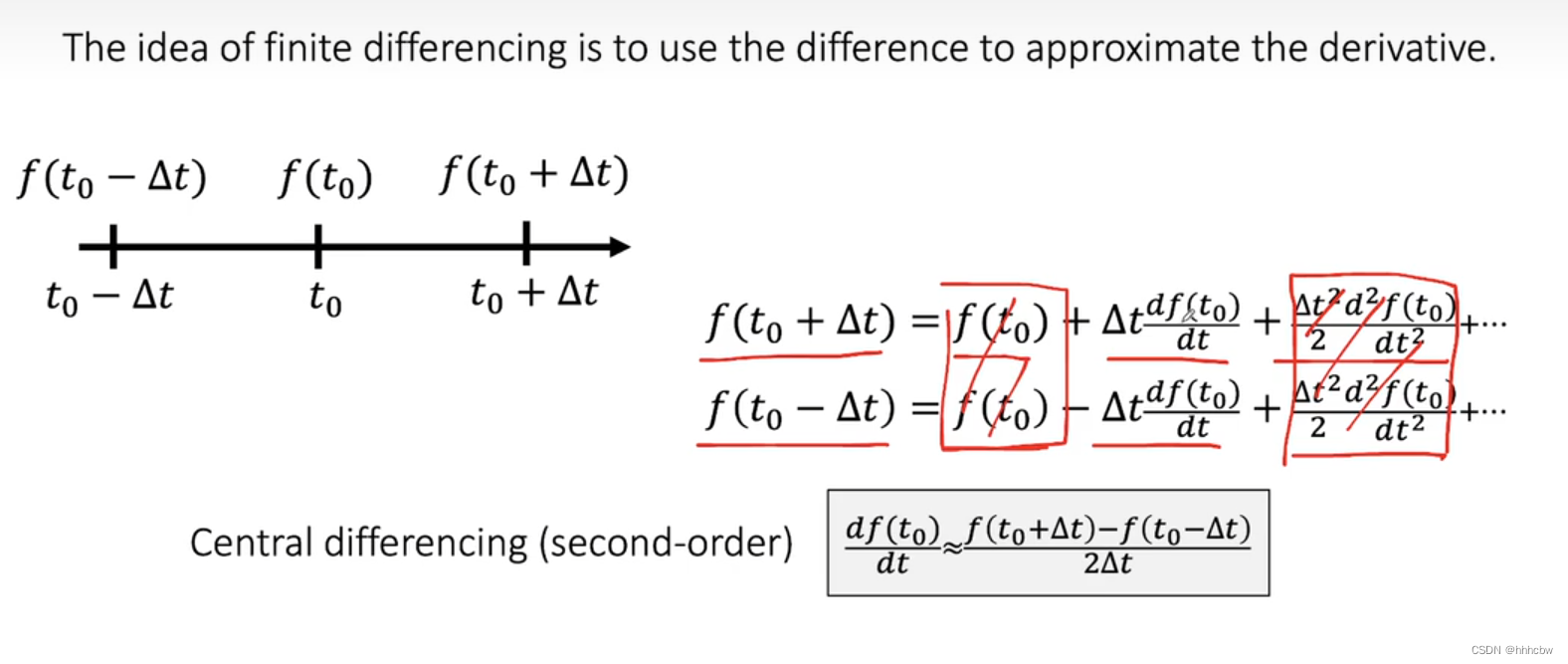
可以利用泰勒展开,求出离散化的前向导数和后向导数(一阶误差)

我们将上下两个泰勒展开求和,可以得出二阶误差的一阶导近似
二阶导数
我们可以通过求出前后 0.5 的一阶导近似,求出当前位置的二阶导近似
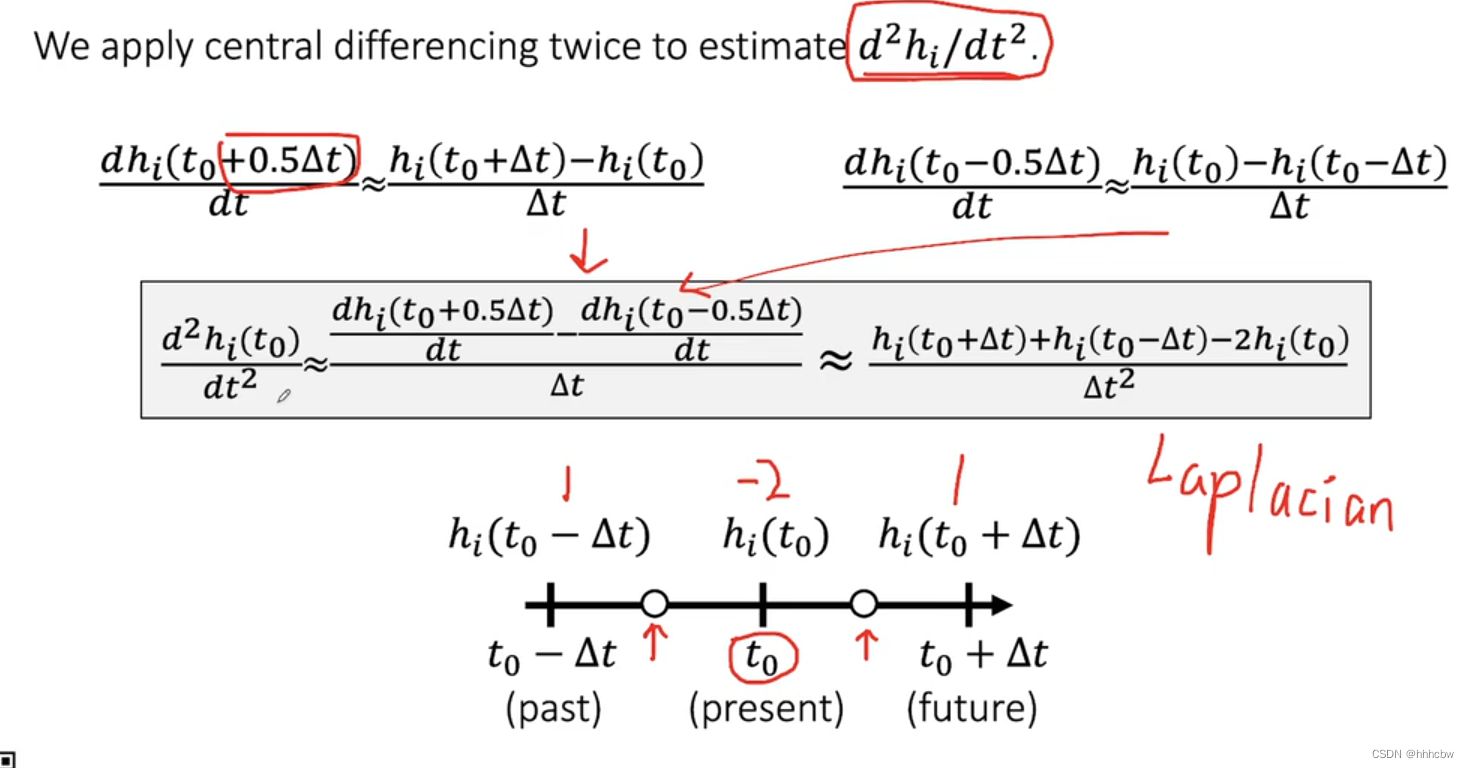
同样,我们也可以计算出 d 2 P / d x 2 d^2P/dx^2 d2P/dx2
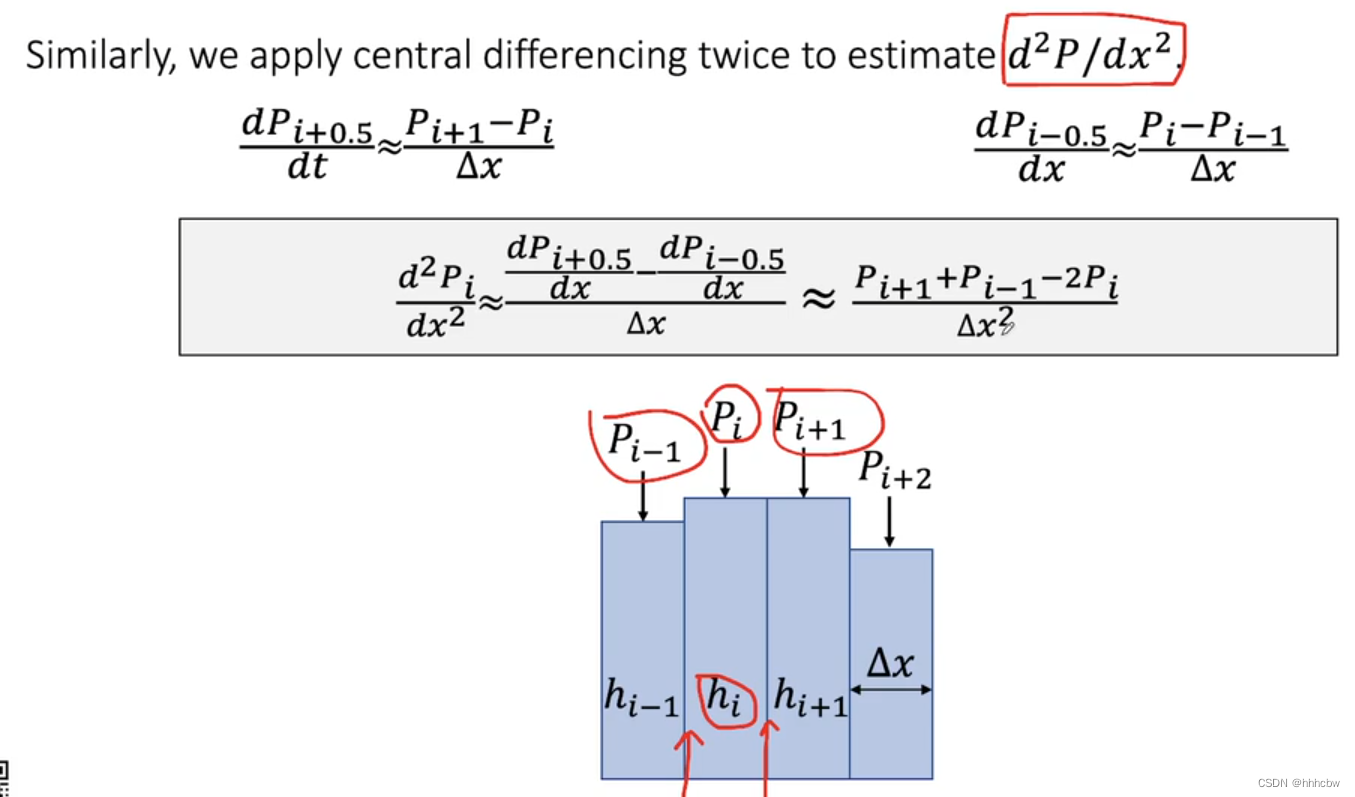
Discretized Shallow Wave Equation
利用上面的一阶导和二阶导的离散表示,我们可以得到离散化的Shallow Wave Equation

由于所有位置水的总体积和应该是不变的(一个常数),而按照上面离散的Shallow Wave Equation得到的水的体积并不是一个常数。

这里有两种方法解决。
Solution 1
一种方法是,将 h i h_i hi 拆分,因为水是和周围两个格子产生交换。
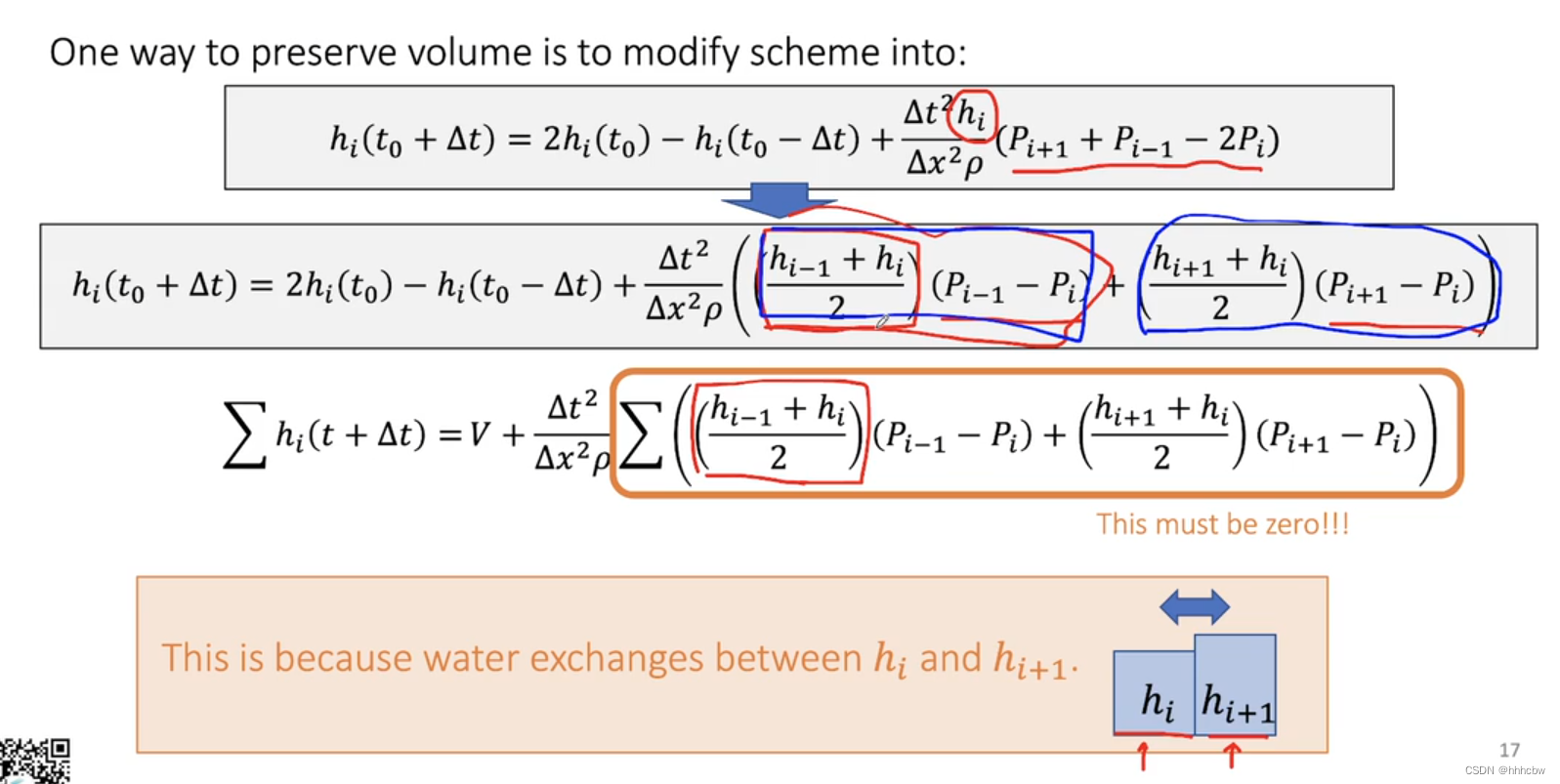
Solution 2
还有一种更简单的方式,就是将所有的 h i h_i hi 看成是一个常数 H H H,这样最后得到的水的总体积和也是常数

Pressure(压强)
P i = ρ g h i P_i = \rho g h_i Pi=ρghi,带入 Solution 2 的公式,我们可以直接用常数 α \alpha α 替换掉 △ t 2 H g △ x 2 \frac{\triangle t^2 H g}{\triangle x^2} △x2△t2Hg

Viscosity(粘滞)
和刚体模拟类似,我们要考虑动量衰减,即粘滞

算法
未考虑边界
未考虑边界的算法流程如下

考虑边界
真实情况下,不可能是无边界的。对于边界的处理有两种方式,一种是当做常量 H i + 1 H_{i+1} Hi+1 进行更新(Dirichlet boundary),另一种是认为边界与边界相邻的高度是相同的(Neumann boundary),这样直接消去。

那么使用 Neumann Boudaries 的算法流程如下

也可以扩展到 3D

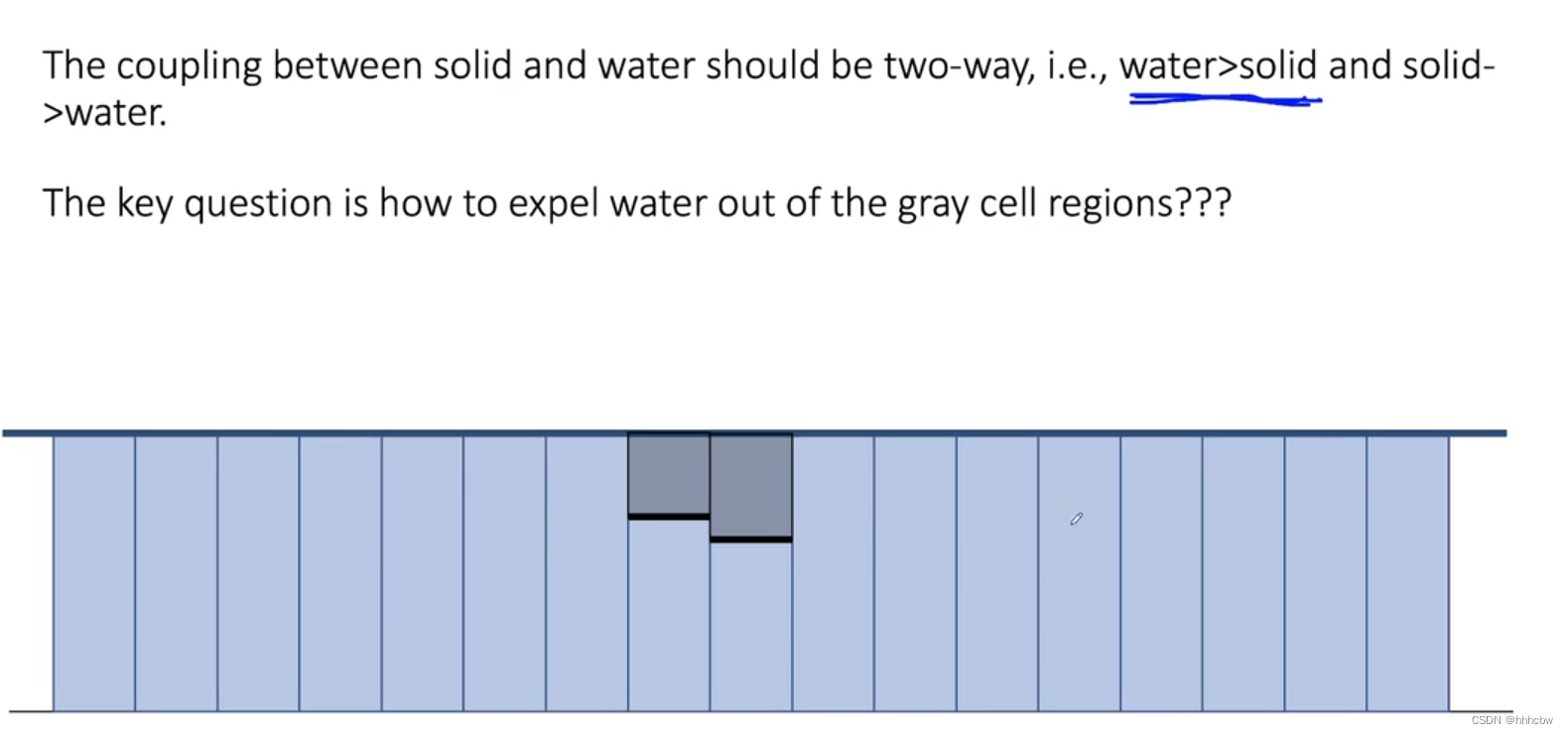
Two-Way Coupling
Two-Way Coupling 就是解决将一个刚体放入流体中,要如何更新高度场与刚体的速度和位置。解决问题的关键是如何将水从灰色格子区域中排出。
更新流体的高度场
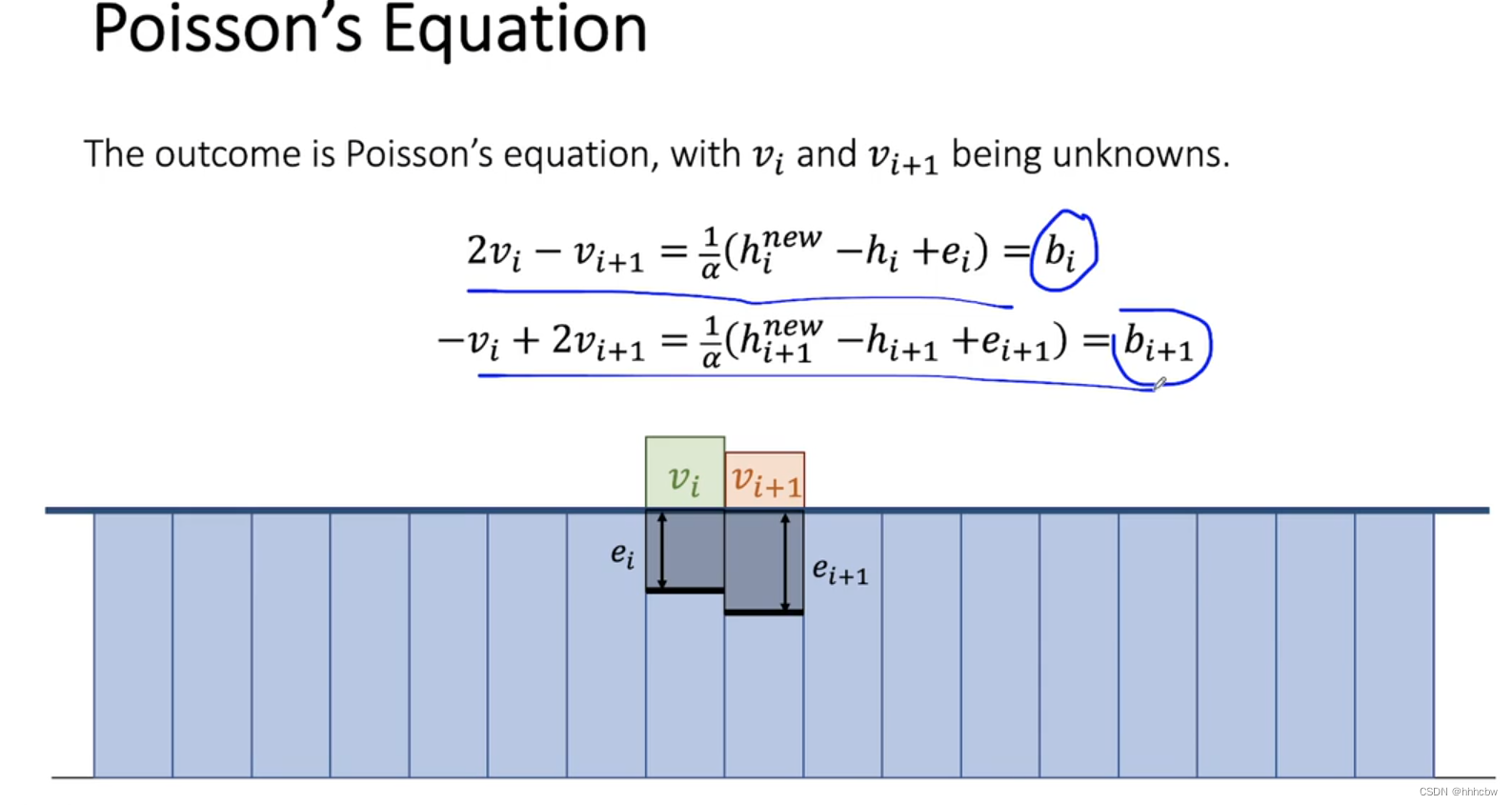
想法是使用一个虚拟高度 v i v_i vi,而 h i r e a l n e w = h i − e i h^{real_new}_{i}=h_i - e_i hirealnew=hi−ei, e i e_i ei 是由刚体陷入水中的位置得到。因为要把水排出,其实可以想象成有一个更高的水柱,要向周围排水。
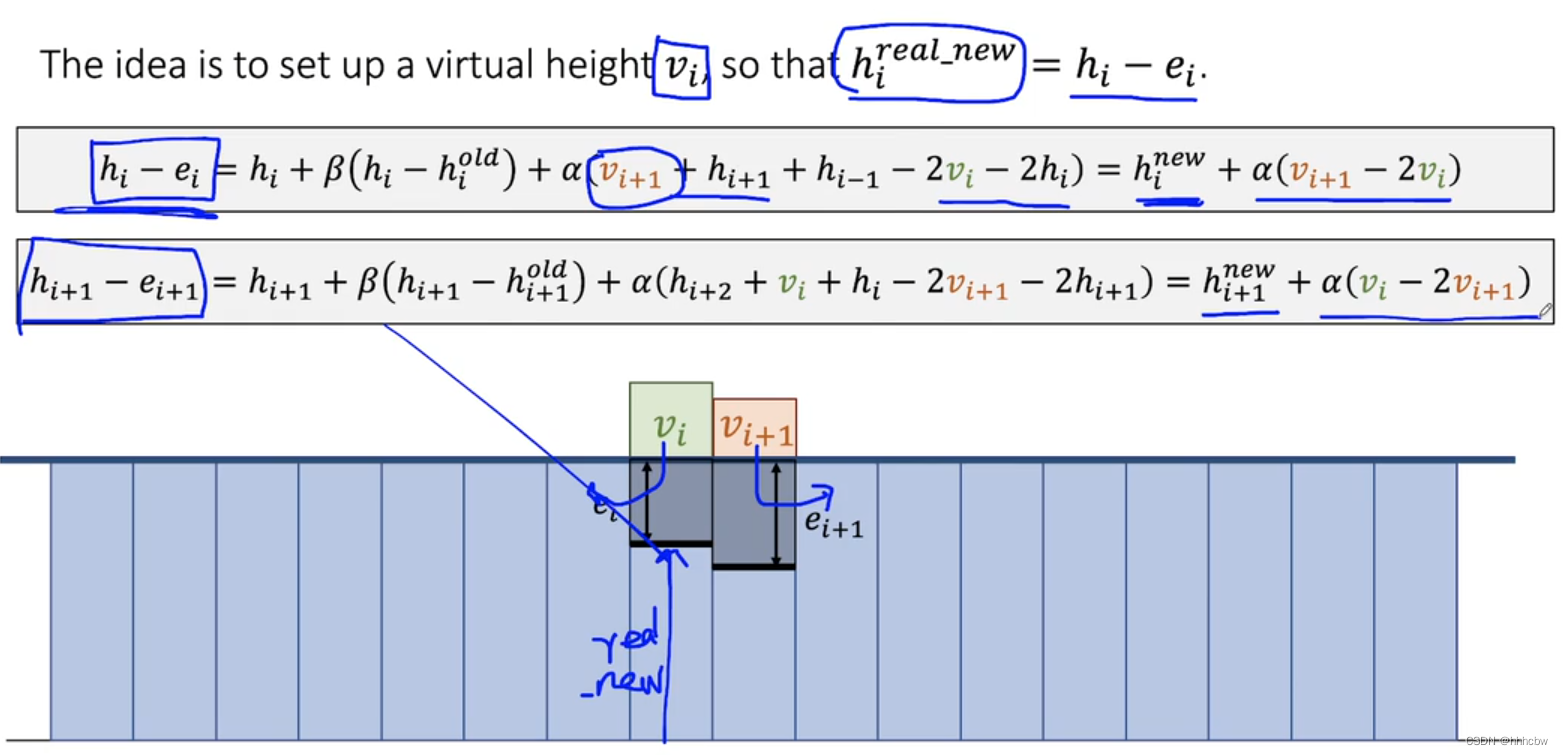
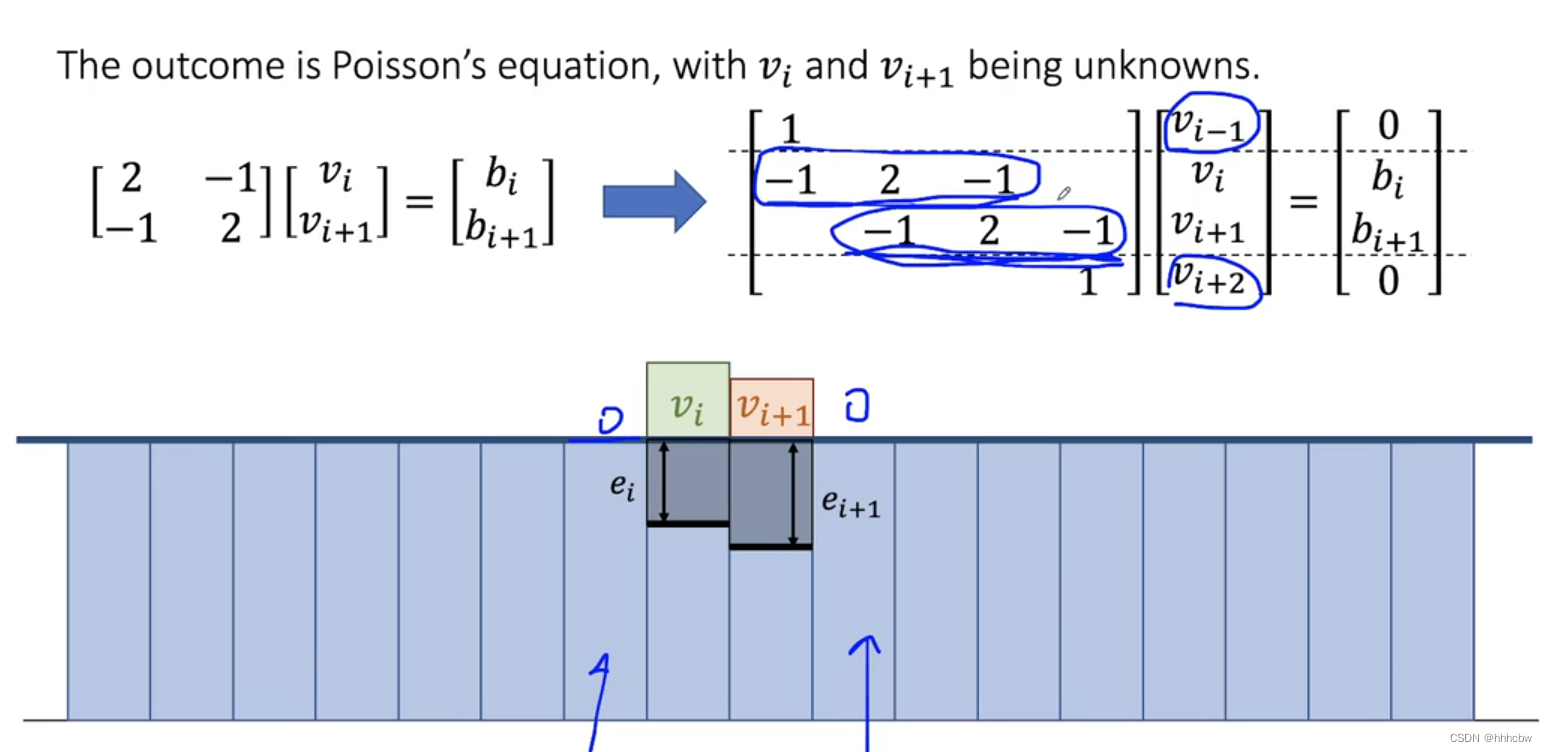
由此可以得到一个 Poisson’s Equation,可以求解出 v i v_i vi 和 v i + 1 v_{i+1} vi+1,然后代入更新高度场。
可以把 v i − 1 v_{i-1} vi−1 和 v i + 2 v_{i+2} vi+2 加上,我的理解是这样使得矩阵对称正定,更容易求解。
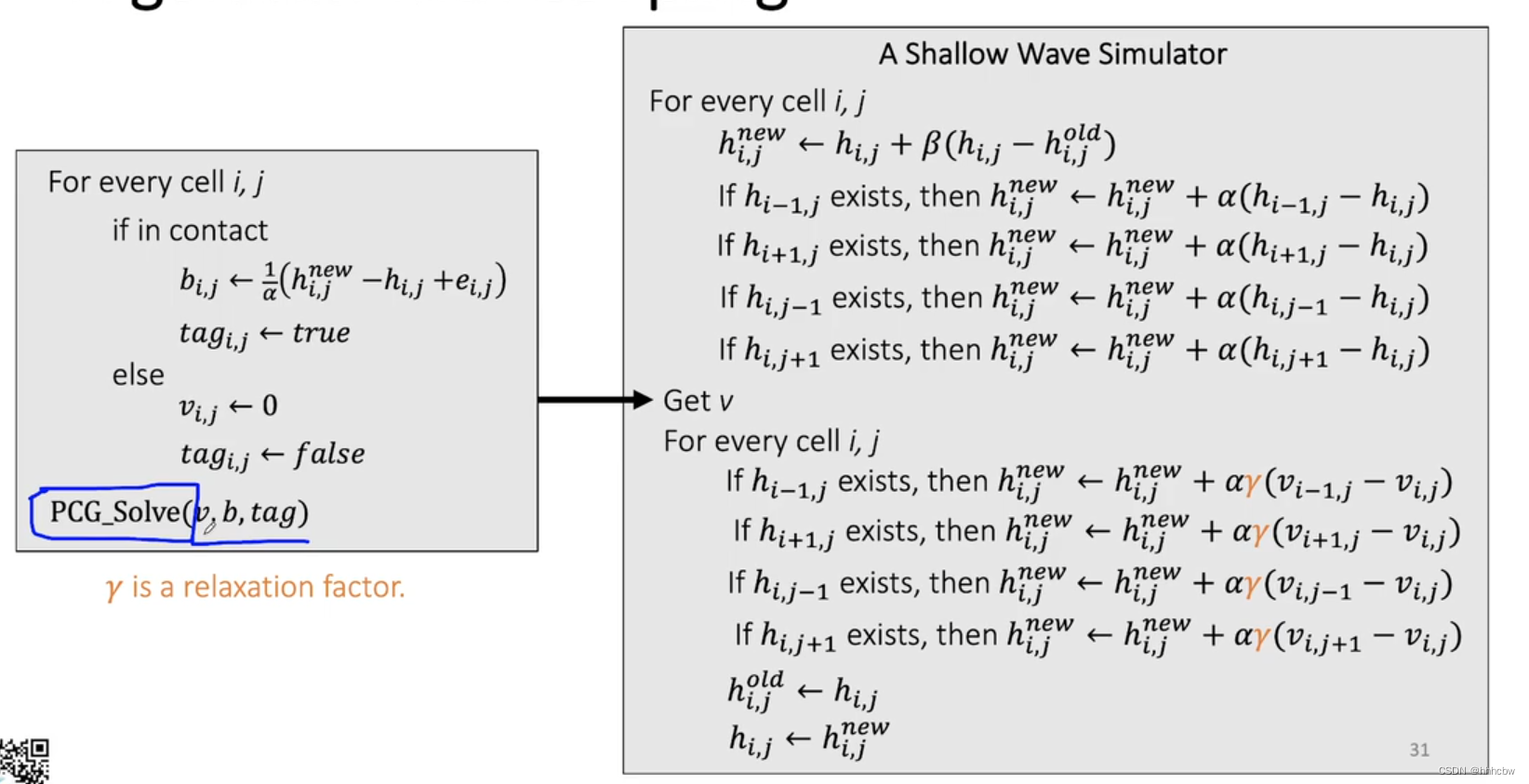
算法
下面是加上虚拟高度的Shallow Wave Simulator,这里 Poisson’s equation 使用共轭梯度法求解。乘上系数 γ \gamma γ 的目的是,目前算法是显式积分,所以存在不稳定性。
刚体更新
刚体受到一个向上的浮力,其力大小如下图所示,之后按照刚体模拟的方式更新其速度和位置即可。