论文研读

Comparison of EEG based epilepsy diagnosis using neural 
networks and wavelet transform

Abstract

癫痫病是一种常见的精神疾病。

本文中，创建一个单一的诊断癫痫的指令。包括两个步骤。

首先，采用低通滤波器对数据进行预处理，设计3个不同频段的中通滤波器和多层神经网络;

第二步，利用小波变换技术对数据进行处理。特别的是，本文提出了一种用于癫痫诊断的多层感知器神经网络分类器，该分类器需要正常数据和癫痫数据进行学习，但该分类器可以识别正常疾病、癫痫，甚至是学习示例中教的其他疾病。

同时，从小波变换和非小波变换两方面评价了脑电图信号的利用价值。

最后，评价结果表明，使用小波变换和不使用小波变换对癫痫数据函数改进的影响因子相对统一，但最终表明，使用感知器多层神经网络可以为专家提供更高的精度系数。

1. Introduction

癫痫的介绍；

癫痫可分为原发性癫痫和局灶性癫痫两种。

来自大脑区域的信号分为局灶性或非局灶性。来自异常脑细胞的信号称为局灶信号，来自正常脑细胞的信号称为非局灶信号。

癫痫疾病的检测是通过区分和检测局部信号和非局部信号来实现的。

某些信号处理技术已经被开发用于通过区分局灶性和非局灶性信号来检测癫痫疾病。患者还需要在手术前对病灶信号进行严重性分析。严重程度可能是“早期”或“晚期”，严重程度为“晚期”的患者需要手术治疗。脑电信号的分解将帮助放射科医生通过从每个分解的子带层中提取的特征来检测信号的焦点行为[2]。癫痫或脑相关疾病的自动识别和检测是临床医生和研究科学家面临的主要挑战

一般来说，神经科专家或脑外科医生会检查脑电记录，以检测癫痫活动。因此，开发一种可靠的、自动化的癫痫发作检测技术是至关重要的。脑电信号的自动判读在脑部疾病的诊断和治疗中是最重要的研究领域之一。有不同的技术可以读取大脑活动，包括脑电(EEG)、脑磁图(MEG)、功能磁共振成像(FMRI)和功能近红外光谱(FNIRS)。因为神经元通过最终到达大脑表面的电信号相互通信，所以EEG被用来通过传感器(称为电极)来捕捉大脑活动[3-5]。近年来，工程学、神经科学、微电子学、生物工程和神经生理学等多学科领域的研究人员致力于将脑电信号提供的所有信息应用于许多应用，如外部设备控制、通信和医疗诊断。基于脑电的信号处理技术对于诊断和监测神经性大脑疾病至关重要，因为它们有助于反映人类大脑中神经元的电活动或障碍。脑电是一种有效的非侵入性方法，常用于脑活动监测和癫痫诊断。

如表1所示，大脑有5个可以用脑电信号测量的频段，每个频段都与大脑的不同精神状态有关[7]。

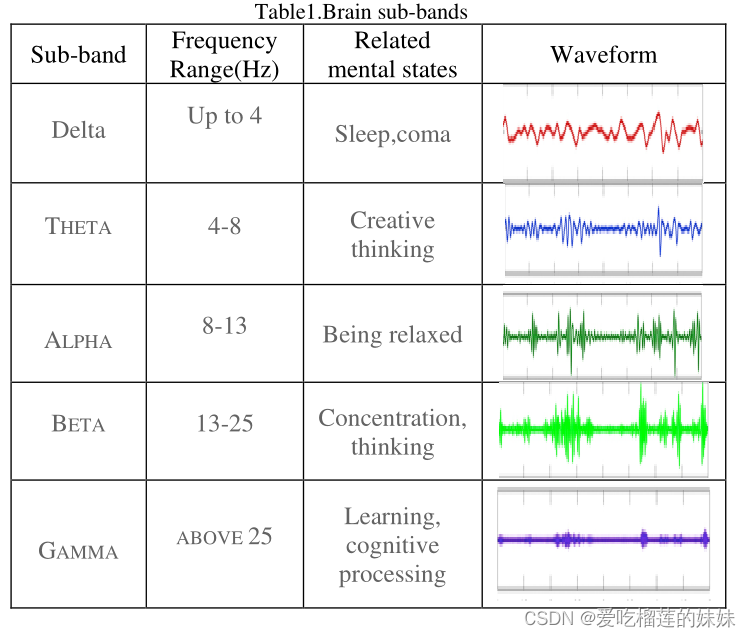
癫痫的另一个定义是，它是两次或多次非刺激性癫痫发作的复发，间隔超过 24 小时。研究还表明，全世界约有 4% 的人在其一生中患有癫痫症，而其中只有 1% 的人会患上癫痫症。

癫痫与中枢神经系统 (CNS) 相关，其中存在异常的大脑活动 [8]。这种不寻常的活动可能发生在大脑的某个部分或整个大脑。结果：癫痫发作、意识丧失、过度暴露于情绪和异常行为，可能发生在任何人身上，不分性别、年龄或种族。症状：凝视、精神错乱、无法控制的身体颤抖、意识丧失、恐惧等心理症状等。

癫痫发作的分类是在大脑异常活动开始的部分进行检查。根据国际抗癫痫联盟(ILAE)的规定，癫痫的诊断至少需要一次无刺激发作，或考虑癫痫复发的风险或诊断癫痫综合征。小儿癫痫是一种高度可变的疾病，因为综合征的年龄相关表达需要特定的诊断、评估和治疗。儿童癫痫与成人癫痫在许多重要方面存在差异，主要与特定癫痫综合征的年龄相关表达有关。这就产生了许多与癫痫诊断、分类、确定病因的评估以及治疗指南相关的重要考虑因素。对这些因素的良好理解将有助于建立准确的癫痫诊断，进而指导作出适当的检测和治疗决定。这是一种由大脑突然功能障碍引起的严重的经常性癫痫发作。

癫痫发作会意外地扰乱正常的大脑功能。大多数患者还遭受许多其他不可预测的癫痫副作用，如记忆力丧失、抑郁和其他精神障碍。因此，在癫痫的早期阶段进行识别，帮助医生采取适当的措施，防止意外后果，确保患者的健康是非常重要的。因此，癫痫发作的自动检测和脑电信号的癫痫检测已成为近几十年来的一个活跃的研究课题[11]。脑电是临床诊断癫痫常用的无创性辅助检查方法。然而，对于神经科医生来说，长时间地从脑电中识别癫痫发作是一项非常繁琐、费力、耗时和昂贵的任务。因此，有必要开发一套可靠的癫痫自动检测系统，以显著提高癫痫患者的生活质量。

癫痫根据症状的类型和对大脑的受累程度分为两大类:全面性和局部性。一般类别包括癫痫波覆盖整个大脑并涉及整个大脑，而局部类别则包括癫痫波仅影响部分大脑[13]。在以往的研究中，人们注意到执行功能是影响阿尔茨海默病、多发性硬化症(MS)、注意缺陷多动障碍(ADHD)和癫痫等各种疾病患者最重要的大脑认知活动，不幸的是，这些活动损害了他们的功能。有研究结果表明，对癫痫患者进行额叶区手术有助于改善其某些功能，如提高意识、缩短发作间隔等。理想情况下，本研究设计的模型可以提高复发性癫痫发作患者的诊断水平，并且对[14]型癫痫发作有诊断困难。两种方法分别对癫痫预测因子(灵敏度、特异性、准确性等)进行评估，如使用小波变换和不使用小波变换的数据，最后设计一个通过接收脑电图信号来检测癫痫的系统。小波变换是应用于各种科学领域的重要数学变换之一，其一般方程如下

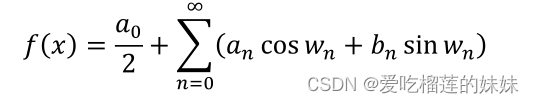
小波(Ψx)函数的性质包括:

a)必须适当地限制时间。

B)均值必须为0。

C)具有非零状态:、

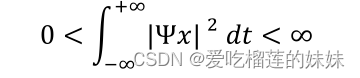
1 - 1.所提方法的概述

本研究总结如下步骤。首先，介绍以前的研究。然后，描述了本研究中使用的数据集。在下一步，我们提出的方法解释，包括预处理，信号处理，特征提取和分类。最后，将本文方法的结果与其他方法进行比较。

2.相关的工作

Tesimorta et al提出了一种基于离散小波变换(DWT)的癫痫发作自动检测方法，将脑电图记录划分为特定的子带并提取特征。然后将这些特征作为训练支持 向量机(SVM)分类器的输入向量。它们的材料和方法包括四个阶段:分割、小波分析、特征提取和分类。第一步，将每个患者活动的长期脑电图记录分为2秒窗口。然后，对脑电信号的每个部分进行5级小波分析，将每个信号分成若干个频带。在下一步中，从每个子带计算创建属性向量的5个属性，最后，属性向量用于教SVM2分类器[14]。

在Kumar和Hyderbank的研究中，使用了两种技术来使用支持向量机对脑电抽搐和非抽搐信号进行分类。在这两种技术中，输入模式被细分为子模式集。在基于子模式的主成分分析(SpPCA)的情况下，通过对每个子集应用PCA3来提取属性。当这些子集的属性提取完成后，将提取的属性按照模式划分顺序组合，形成最终的属性向量。其次，对前一步提取的特征进行主成分分析，进一步降维，提取整 体特征[17]。Schubb和Guttag提出了一篇论文，将机器学习算法‘支持向量机’应用于头皮脑电数据集，以诊断癫痫发作，该方法在实验数据方面获得了96%的准确率[18]。

Rahul Sharma等人利用三阶累积量函数自动检测局灶性脑电信号。利用局部敏感判别分析(LSDA)方法从脑电信号中提取特征，然后利用支持向量机(SVM)分类技术对这些特征进行分类。作者在伯尔尼-巴塞罗那脑电数据集上获得了99%的最大分类准确率[19]。Siddharth等人提出了一种利用滑模奇异谱分析方法区分焦点信号和非焦点脑电信号的方法。从脑电信号中计算重构的成分特征，并利用径向基函数神经网络对特征进行分类。

作者在脑电上测试了他们提出的方法。对巴塞罗那脑电数据集的信号进行识别，平均准确率为99.11%，平均敏感度为98.52%，平均特异度为99.7%[20]。为了从脑电信号中提取25个幅度特征，Rahul Sharma等人提出了一种双谱方法。利用LSDA方法获取这些特征，然后使用支持向量机分类方法对计算出的特征进行分类。作者对巴塞罗那脑电数据集的脑电信号进行了10次交叉验证，分类准确率达到96.2%[21]。

Nigam和Graupe建议使用多级非线性滤波和人工神经网络(ANN)相结合的基于脑电的计算机辅助诊断癫痫；他们提出的技术获得了97.2%的准确率[22]。

Kannathal等人。比较了不同的熵算法，提出了用不同的熵值区分正常脑电和癫痫脑电信号；采用自适应神经模糊推理系统(ANFIS)进行分类，准确率达到92.2%[23]。此外，Sadati et al.。用自适应神经模糊网络代替ANFIS进行癫痫诊断，利用离散小波变换(DWT)子带的能量进行特征提取。然而，他们提出的方法的准确率很低(约85.9%)[24]。Dalal等人探索了柔性解析小波变换(FAWT)来求取脑电信号的分解系数。这种非平稳变换在每个尺度级别上产生了分维特征。使用Kruskal-Wallis统计检验对该方法进行了测试，在巴塞罗那脑电数据集上获得了89.1%的平均分类准确率[25]。

Deivasigamani等人分析了一种基于软计算的自适应神经模糊推理系统(ANFIS)分类方法，该方法利用聚焦信号和非聚焦信号的特征值来区分它们。将其应用于700个脑电信号，其中694个信号被正确分类。作者获得了99.1%的检测率[26]。Abhinaya等人研究了一种从脑电信号中提取基于熵的特征的方法。利用序贯正向特征选择方法对提取的特征进行优化。然后，将线性回归模型中的支持向量机应用于优化的特征，以区分局灶性和非灶性脑电信号。

作者通过将其应用于开放访问的EEG数据集，获得了92.8%的分类率[27]。易卜拉欣等人。分析了一种基于小波和Shannon熵的癫痫诊断方法。在他们的研究中，使用了支持向量机、LDA、人工神经网络和k近邻作为分类器[28]。

GruszczyńSka等人。提出了一种基于学习的递归量化分析方法对脑电信号进行分类。结果采用主成分分析进行可视化处理。利用支持向量机对获得的结果进行分类[29]。Anuragi和Sisodia提出了基于方法的机器学习方法和小波变换来治疗酒精使用障碍。这项研究的目的是对酗酒者和健康人进行自动分类。研究中使用了支持向量机和朴素贝叶斯方法[30]。Mutlu提出了一种利用Hilbert振动分解来治疗癫痫的方法。在研究中，选择最小二乘支持向量机作为分类器。研究目的是区分正常和癫痫个体之间的信号。时间、精度和接收器操作特性被选为评估参数[31]

阿尔萨尔曼等人。提出了一项使用小波傅里叶分析从脑电图信号中检测睡眠纺锤波的研究。最小二乘 SVM 用于分类器 [32]。 Asghar Zarei 等人。使用离散小波变换（DWT）和正交匹配追踪（OMP）技术。 d 从脑电信号中提取不同的系数。然后，使用 DWT 和 OMP 系数计算一些非线性特征，例如模糊/近似/样本/字母和正确的条件熵，以及一些统计特征。三个广泛使用的脑电图数据集被用来评估所提出技术的性能[33]。最近，Yavus 等人。探索了 Mel 频率倒谱系数 (MFCC) 和广义回归神经网络在区分正常和癫痫脑电图记录中的效用 [34]。

Mehdi Omidvar 等人。使用离散小波变换（DWT）通过将EEG信号划分为五个子带来提取EEG信号的特征。所提出的技术还包括用于选择更有效特征的遗传算法方法，最后，通过人工神经网络（ANN）和支持向量机（SVM）两种策略进行分类。比较了两个分类器的性能，其中模拟结果表明，所提出的癫痫发作检测策略准确性优于文献中的其他类似方法[35]。

3. 数据库

对于这种方法，使用了来自波恩大学数据库 [36] 的癫痫数据。该数据库包括5种不同的注册模型，设置为500个，每个有100分，分别是：

A) 睁眼非癫痫记录 B) 闭眼非癫痫记录 C、D) 使用放置脑头皮电极进行记录 E) 癫痫发作期间记录的数据。

每次录音时长为 23.6 秒，采样频率为 173.6 Hz。在本文中，使用了模型 B 和 E。

首先不使用小波变换函数，然后使用分解级别为8的母小波变换函数。表2总结了数据库的详细信息：

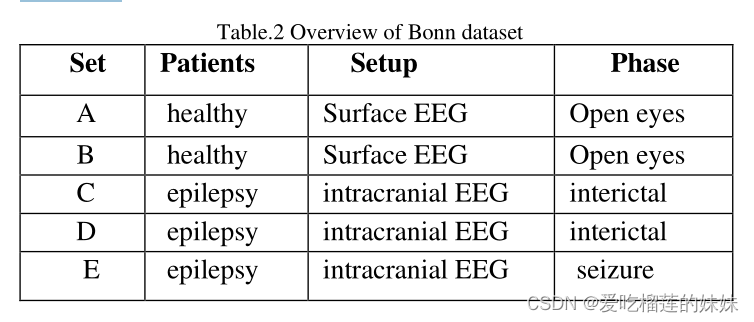
本研究中使用的数据库是波恩大学网站上的开放访问数据库。

4. 方法

从上述数据库接收数据后，数据预处理就开始了。在此步骤中，设计并实现了两种方法的70hz低通滤波器。然后，在数据处理步骤中，通过设计一个单独的中通滤波器来提取alpha、beta和gamma频段。在特征提取步骤中，提取了频率中值(FMD)、频率均值(FMN)、频率比(FR)、波形长度(WL)等特征。最后，设计了多层感知器神经网络(MLP)分类器。在对该分类器进行实验并获得预期结果后，分别采用小波变换方法。图1给出了建所提方法的示意图。

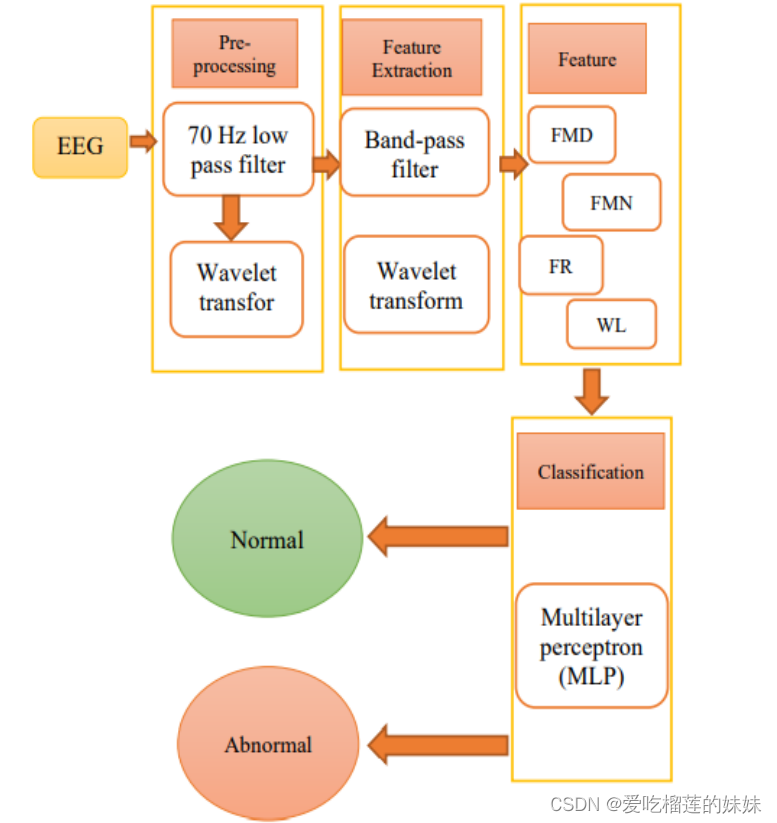
 4 - 1.信号预处理

预处理步骤分别采用小波变换和不采用小波变换的70hz低通滤波器对两阶段采集的原始脑电信号进行预处理。该滤波器采用FDATOOL工具箱设计，利用MATLAB 2020软件中的wave菜单工具进行小波变换。为了用小波变换函数去噪，我们在同一个小波变换工具箱中使用去噪部分。在本节中，小波通过匹配子信号(EEG信号)和母信号(小波信号)独立猜测噪声，如果它们不匹配，则从较低层次去除细节，同时保留一般性。

4 - 2.信号处理

在这一步中，在 alpha、gamma 和 beta 波段上，一个带通滤波器：Fpass1 = 25HZ，Fstop2 = 71HZ，Fstop1 = 24HZ 并且对于 gamma 波段，一个具有最小阶值的带通滤波器：Fpass2 = 70并且使用了 Fstop = 71HZ。通带和阻带纹波分别为 0.1 和 0.01。对信号进行小波变换处理，得到滤波系数，包括近似系数和细节系数，然后分别计算alpha-beta和gamma波段的不同层次的细节系数和一般系数。这些系数的输出信号是使用 MATLAB 时域中的“wrcoef”命令计算的。

4-3.特征提取

特征提取是癫痫发作检测中必不可少的步骤，用于通过标准癫痫数据建立癫痫检测模型，并根据实际采集的脑电信号数据进行癫痫检测。小波变换将信号分解为母小波和尺度函数的缩放和平移版本。离散小波变换（DWT）在最近的癫痫尖峰和癫痫检测方法中得到了频繁的应用，并取得了可喜的成果。特征提取的效果与癫痫检测的准确性密切相关，因此改进特征提取势在必行。为了分别记录癫痫信号，EEG 记录大约需要 20 分钟，包括光刺激和睁眼和闭眼的休息时间。在本文中，尝试分别在每个 alpha、gamma 和 beta 频带中提取癫痫和非癫痫数据的频率和时间领域的四个重要特征，它们分别是：FMD4、FMN5、FR6、和WL7。提取的特征如表3所示。

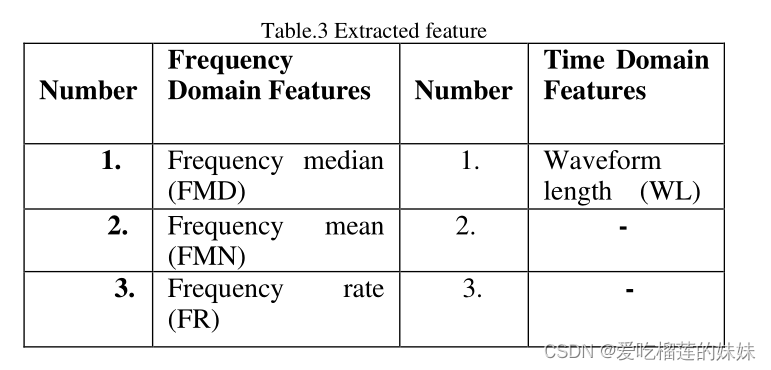
 在癫痫患者中，由于脑频率较高，中位频率和平均频率增加，频率比降低。在波形长度特征中，变化被测量，下一个样本的绝对值从前一个样本减少，如果信号是平滑的，没有太多的变化，这个属性变为零。因此，在癫痫疾病中，当紊乱的熵较低且脑振荡相同时，波形长度减小。

 香农熵用于使用小波变换计算熵，小波变换根据比特变化计算熵[37]。

4-4 分类

对癫痫信号进行分类，采用10层输入、5%验证的多层神经网络，该分类器在多层神经网络中准确率达到95.5%，验证结果如图2所示。

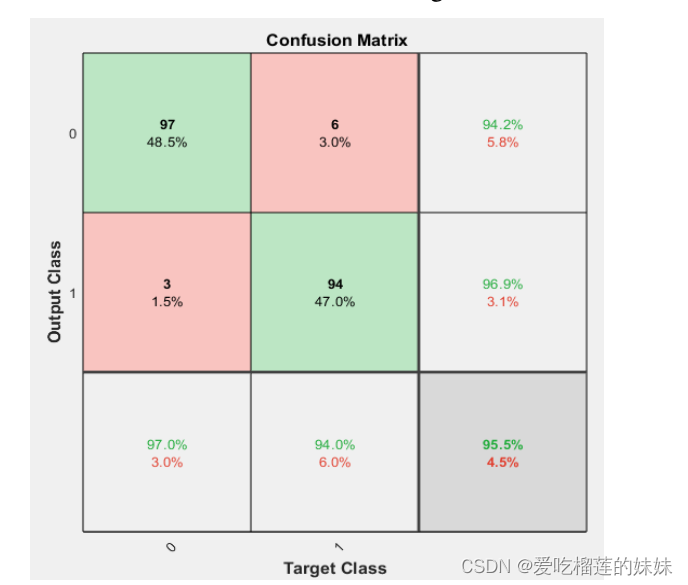
图(2):感知器多层神经网络的验证值和准确性

 然后采用8级小波变换和4级分解和香农熵进行熵值计算。该方法对癫痫的诊断准确率为91%，验证结果如图3所示。

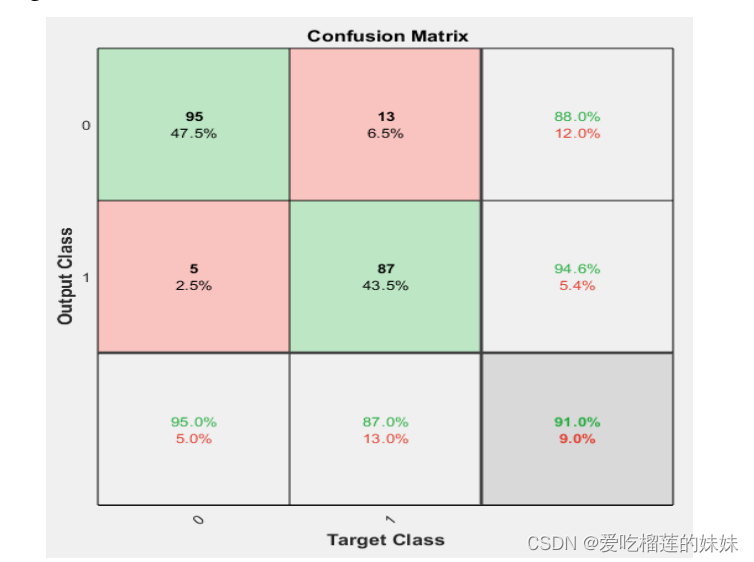
 图(3):小波变换后的验证值和精度

5. Discussion

如前所述，癫痫发作的原因包括流行病学、病因学、急性中风、脑感染以及某些药物的破坏性作用。在以往的研究中，有研究者使用EEG信号与FMRI联合检测生理值[8]，也有研究者倾向于使用神经反馈治疗癫痫发作[36]。近年来，研究中提出了以功能动力学为重点的先进方法来帮助癫痫患者。例如，在各种研究中，在癫痫患者的θ频带中研究了SL参数，其对癫痫的分类敏感性为62%，特异性为76%。近年来，由于脑电图信号反映神经脑活动，脑电图信号分析技术得到了长足的发展，已成为诊断神经脑疾病的重要工具。本研究的目的是验证EEG在两个不同实验阶段测量的生理信号的预测价值。在波恩数据集上进行的几次测试也显示了与其他近期方法相比具有脑电图特征的预测模型与临床诊断相比取得了显著进展，并帮助我们诊断脑电图信号中是否存在癫痫症状。在第一步，利用多层感知器神经网络(MLP)分类器，分别检测α、β和γ频段的癫痫和控制信号，获得95%的准确率检测癫痫信号。

然后使用小波变换函数，对alpha、beta和gamma频段的信号进行重新检测，获得了约91%的检测癫痫信号的准确率。

与其他研究相比，本研究成功地从脑电图信号中获得了一种更简单的癫痫评估方法，并获得了合适的准确性等参数。

6. 结论

由专家医师对长期脑电图记录进行目视检查来进行癫痫发作评估是一种非常昂贵和耗时的方法。针对这些问题，本研究提出了一种新的基于脑电信号的癫痫发作检测算法。该研究的主要力量是用多层感知器神经网络分类器对可用样本进行描述，并与小波变换函数进行比较。

未来需要更大样本量的研究来证实我们的发现并推进结果在这项研究中，评估了使用 EEG 测量的生理信号的诊断价值。该研究还成功地提取了 (FMD)、(FMN)、(FR) 和 (WL) 等特征。 )FMD( 和 )FMN( 是中值和平均频率，是通过对所需信号的傅里叶变换获得的，在癫痫患者中，这两个特征会增加，因为大脑频率高于正常人。 （FR）或频率率是指大脑的高低频比，由于癫痫患者的大脑频率高于正常人，因此频率率降低。

但是（WL）或波形长度是一种时间特征，它从之前的样本中减去后续信号样本的绝对幅度，并将其相加，实际测量信号的变化和复杂性，并且在患有癫痫的人中，由于熵减少和大脑中类似的波动（WL）会减少。这些特征的计算为医生在癫痫患者中诊断和使用该方法提供了良好的信息。

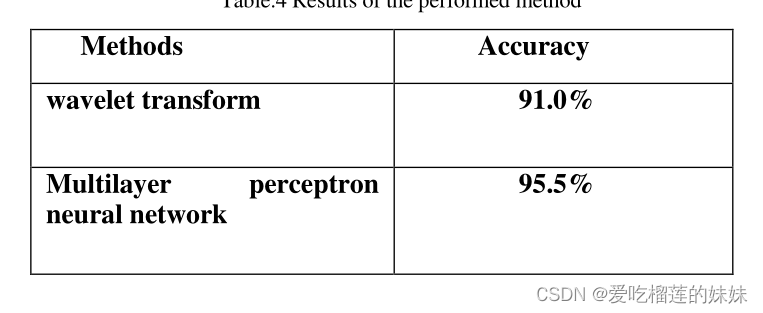
根据本文进行的研究，尽管本文中使用的两种方法之间没有太大差异，如表4所示。第一步使用多层感知器神经网络（MLP）进行的实验比使用小波变换函数进行的实验获得了更高的精度。近年来，越来越多的新方法开始应用于癫痫的自动检测。更快、更准确的癫痫检测模型的开发将有助于临床诊断中的癫痫检测技术以及便携式集成癫痫检测设备的开发。因此，一种简洁高效的癫痫检测模型将成为未来发展的必然趋势。

表 4 执行方法的结果