水文模型模拟效果评价指标
- 1 皮尔逊相关系数(Pearson’s correlation coefficient, PCC)
- 1.1 简介
- 1.2 MATLAB实现代码
- 2 百分比偏差(Percent bias, Pbias)
- 2.1 简介
- 2.2 MATLAB实现代码
- 3 纳什效率系数(the Nash-Sutcliffe efficiency coefficient, NSE)
- 3.1 简介
- 3.2 MATLAB实现代码
- 4 克林-古普塔效率系数(Kling-Gupta efficiency coefficient, KGE)
- 4.1 简介
- 4.2 MATLAB实现代码
- 5 决定系数R^2(Coefficient of Determination)
- 5.1 简介
- 5.2 MATLAB实现代码
- 6 归一化均方根误差(NRMSE)
- 6.1 简介
- 6.2 MATLAB实现代码
- 7 均方根误差与观测值标准差的比率(RSR)
- 7.1 简介
- 7.2 MATLAB实现代码
- 模型评价
- 参考
1 皮尔逊相关系数(Pearson’s correlation coefficient, PCC)
1.1 简介
评估模拟径流与观测径流间的线性相关性:

1.2 MATLAB实现代码
MATLAB实现代码如下:
function PCC = GetPCC(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% PCC 皮尔逊相关系数(Pearson’s correlation coefficient, PCC)if length(Qs)==length(Qo)COV = cov(Qs, Qo);PCC = COV(1,2)/std(Qs)/std(Qo);
elseerror("实测径流和模拟径流长度不等");
endend
2 百分比偏差(Percent bias, Pbias)
2.1 简介
百分比偏差Pbias(%),又称相对误差,表示测量模拟的水流的百分比偏差大于或小于相应的推断的自然水流,越接近0模型效果越好:
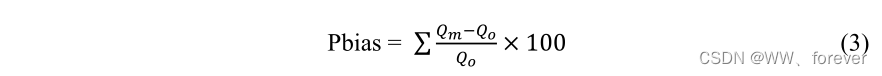
说明: 体现模拟值和实测值的累积偏差,当模拟水文过程与实际趋势贴合情况良好时,PBIAS可更加精确地评估模型总水量平衡的效果。最优值为0,表示模型模拟准确,正值表示模型低估观测值的偏差,负值表示模型高估观测值的偏差。
2.2 MATLAB实现代码
MATLAB实现代码如下:
function Pbias = GetPbias(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% Pbias 百分比偏差/相对误差(Percent bias, Pbias)if length(Qs)==length(Qo)Pbias = sum( (Qs-Qo)./Qo);
elseerror("实测径流和模拟径流长度不等");
endend
3 纳什效率系数(the Nash-Sutcliffe efficiency coefficient, NSE)
3.1 简介
NSE被广泛用于确定水文的总体模型效率,它是根据模型模拟和观测的水流时间序列计算得出的:

说明: 体现模拟径流和实测径流的拟合程度,但会赋予洪峰段更高的计算权重,容易忽视平水期或枯水期的拟合情况
3.2 MATLAB实现代码
MATLAB实现代码如下:
function NSE = GetNSE(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% NSE 纳什效率系数(Nash-Sutcliffe efficiency coefficient, NSE)if length(Qs)==length(Qo)QoAve = mean(Qo);NSE = 1- sum( (Qs-Qo).^2/(Qo-QoAve).^2 );
elseerror("实测径流和模拟径流长度不等");
endend
4 克林-古普塔效率系数(Kling-Gupta efficiency coefficient, KGE)
4.1 简介
KGE测量的是一个点到最优点的欧几里得距离,相关系数(correlation coefficient, PCC)、偏置比(bias ration, BR)和相对变化率(relative variablity, RV)等于1:
取值范围:(-∞,1)

4.2 MATLAB实现代码
MATLAB实现代码如下:
function KGE = GetKGE(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% KGE 克林-古普塔效率系数(Kling-Gupta efficiency coefficient, KGE)if length(Qs)==length(Qo)QsAve = mean(Qs);QoAve = mean(Qo);COV = cov(Qs, Qo);CC = COV(1,2)/std(Qs)/std(Qo);BR = QsAve/QoAve;RV = ( std(Qs)/QsAve )/ ( std(Qo)/QoAve );KGE = 1- ( (CC)^2+(BR+1)^2+(RV-1)^2 )^0.5;
elseerror("实测径流和模拟径流长度不等");
endend
5 决定系数R^2(Coefficient of Determination)
5.1 简介

说明: 模拟值与实测值的线性相关程度,弊端是R2对模拟值整体偏高或偏低的偏差响应不明显
决定系数=1时,表明模拟值与实测值非常吻合。
5.2 MATLAB实现代码
MATLAB实现代码如下:
function R2 = GetR2(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% R2 决定/相关系数R2(Coefficient of Determination)if length(Qs)==length(Qo)QsAve = mean(Qs);QoAve = mean(Qo);R2 = ( sum( (Qo-QoAve).*(Qs-QsAve) )/ ( sum(Qo-QoAve).^2)^0.5/ ( sum(Qs-QsAve.^2)^0.5 )^2 );
elseerror("实测径流和模拟径流长度不等");
endend6 归一化均方根误差(NRMSE)
6.1 简介
6.2 MATLAB实现代码
7 均方根误差与观测值标准差的比率(RSR)
7.1 简介

说明: RSR从最优值0变化到较大的正值,该值越小,表示模型性能越好。
7.2 MATLAB实现代码
MATLAB实现代码如下:
function RSR = GetRSR(Qs, Qo)
% 输入变量
% Qs 模拟径流
% Qo 实测径流
% 输出变量
% RSR 均方根误差与观测值标准差的比率(RSR)if length(Qs)==length(Qo)QoAve = mean(Qo);RSR = ( sum(Qo-Qs).^2 )^0.5/( sum(Qo-QoAve).^2 )^0.5;
elseerror("实测径流和模拟径流长度不等");
endend
模型评价
一般认为,当R2>0.6,NSE>0.5,PBIAS≤±15%以及RSR<0.7时,模型的模拟结果是可信的。
根据 Moriasi et al.(2007)径流模拟评价,RSR、NSE以及PBIAS的建议取值及相应的模型评价等级如下表所示:

参考
1.论文-J2022-High-quality reconstruction of China’s natural streamflow-缪驰远
2.论文-D2022-气候变化下长江流域未来径流与旱涝变化特征研究-岳艳琳