按照下图的算法，似乎可以算出圆周率  等于4：

这个结论肯定是错误的，这篇文章就来仔细解释下。

1 周长和面积

确实，随着不断弯折，圆外多边形看上去越来越接近圆：

那为什么文章开头的结论是错误的呢？我们需要明白，在这个弯折过程中，圆外多边形的周长和面积发生了不同的改变：

• 圆外多边形的周长始终保持不变，并没有逼近圆的周长

• 圆外多边形的面积不断逼近圆的面积，所以看上去圆外的多边形看上去越来越接近圆

1.1 周长不变

将圆的右上角放大，可见外接正方形的边无论折成多少个阶梯，只要恰当地平移这些阶梯，就可以还原出之前的正方形（动图出处）：

也就是说，在弯折过程中，圆外多边形的周长始终为4：

更代数一点，可用数列  来表示弯折过程中外面多边形的周长，很明显该数列的极限为：

这是一个常数数列，该数列的极限为4，这说明弯折过程中圆外多边形的周长是没有发生变化的。

1.2 面积逼近

一开始，外接正方形和圆形的面积大概相差4个直角三角形，也就是下图中蓝色的四个直角三角形。因为圆的直径为1，所以容易推出这四个直角三角形的面积之和为  ，也就是说外接正方形和圆形的面积大概相差  ：

不断地弯折圆外多边形，可以算出这些直角三角形的和是在不断减小的，也就是圆外多边形和圆形的面积差在不断减小：

这说明圆外多边形的面积在不断逼近圆形的面积。

1.3 科赫雪花

综上，之所以得到错误的结论，是我们直觉上认为面积逼近的同时周长也会逼近。这个直觉是错误的，周长和面积并没有绝对的对应关系。来看一个更极端的例子，像下面动图一样，从边长为  的等边三角形开始，可以生成类似于雪花的图像，也称为科赫雪花：

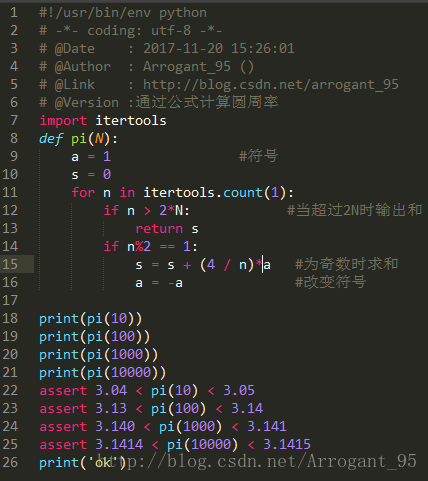
可以证明，科赫雪花的面积的极限为  ，但周长的极限为无穷大，具体细节可以参考这里。

2 另外一个问题

下面来看一个类似的问题，这个问题可以帮助我们思考得更深一些。同样是直径为1的圆，在它的圆周上画满相切的圆：

如果交替地取这些圆在圆周内的部分和圆周外的部分，就构成了一条缠绕着圆周的连续曲线：

上图中的曲线是由8个圆组成的，当然可以用更多的相切圆来构造该曲线。随着相切圆的增加，该曲线的周长会持续缩小，但是到一定程度后周长就不再缩小了：

实际上，该曲线的周长会停留在该数值附近，并不会逼近圆的周长。背后到底是什么原因，使得曲线周长没有逼近圆的周长？

3 切线

在微积分中学习过，在一定的条件下， 点附近的曲线可以用切线来近似（这是《单变量微积分》中的内容）：

3.1 曲线的长度

假如要计算曲线在  之间的长度，可以将把  切成  份，对应的曲线也被分成了  份：

因为切线是对曲线的近似，所以可用每个部分的切线段长度来近似每个部分的曲线段：

进一步细分  ，也就是让  变得更大，可以看到近似的效果会越来越好：

当  时，这些切线段的长度加起来就是曲线的长度。

3.2 错误的逼近

回头来看一下，之前的例子是用折线或者曲线去逼近圆形的周长：

而不是用圆形的切线去逼近圆形的周长，这就是得出错误结论的原因。

3.3 为什么是切线

那为什么圆形的切线才能去逼近圆形的周长呢？这个问题可能需要用整个《单变量微积分》课程来回答。这里就简单说一下重点，可以证明，曲线的切线和曲线之间相差一个 高阶 无穷小，也就是下图标注的  ：

上述说法反过来也是成立的：

在计算圆形周长的例子中，用来近似圆形周长的折线、曲线，它们只和圆形相差了一个无穷小。这里不去深究具体的代数表达式，只需要知道，高阶 无穷小的意思就是比无穷小还要小。也就是说，圆形的切线是最接近圆形的，因为它们之间相差最小（高阶无穷小）。所以，必须用切线才能成功逼近。

文章的最新版本请查看：为什么算出来的圆周率 π 等于 4 ？