582-快速排序算法的思想和性能分析

快速排序算法的思想

在这里插入图片描述

下面是一组待排序的序列，我们现在要使用快速排序算法的思想解决
在这里插入图片描述
1、我们选取基准数，我们把第一个数字当做基准数
进行元素的调整，对于数组来说，我们要涉及1个范围，用起始下标和末尾下标。
我们用L表示左边的起始下标，R表示右边的起始下标

我们用val=46，即首元素，作为基准数
2、从R开始往前遍历，找第一个小于基准数val=46的数字，放到L的地方，
53不小于基准数46，所以我们让R–，R访问到65这个元素，在这里插入图片描述
65不小于基准数46，所以我们让R–，R访问到32这个元素，

32小于基准数46了，我们把32放到L的位置，把46覆盖了，因为46是基准数，我们已经存储到val这个变量上了，不用担心被覆盖丢失，然后L++，L访问到8
在这里插入图片描述

3、从L开始往后找第一个大于基准数val=46的数字，放到R的位置(此时不需要考虑R的位置的元素被覆盖的问题，因为32在刚才已经放在了L之前的位置上了）。
现在L访问的是8,8不大于46，L++
L访问到76
在这里插入图片描述
76大于46，我们把76放到R的位置，然后R–（此时的L位置上的数字不需要考虑被覆盖的问题，因为L位置上的数字76已结放在了刚才R的位置上了)，访问到68

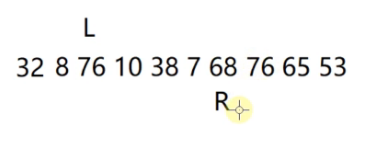
4、然后重复上面的过程
从R开始往前找，找第一个小于基准数46的数字，放到L的位置，
68不小于基准数46，R–
在这里插入图片描述

R访问到7,7小于基准数46，然后把7放到L的位置，然后L++
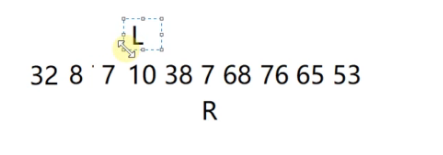
在这里插入图片描述
从L开始向后访问，找第一个大于基准数46的数字，放到R的位置上
10不大于基准数46，L++
L访问到38
38不大于基准数46，L++
L访问到7，此时L==R

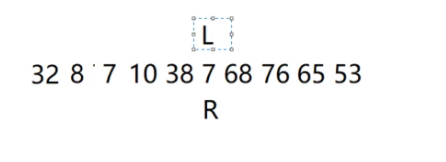
既然有重复的过程，肯定是有循环的。
L= =R的时候，就说明循环结束了，这个位置该存放基准数46了
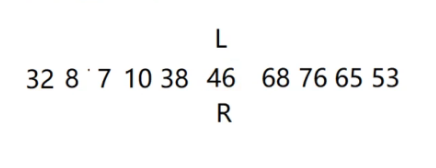
在这里插入图片描述

在这里插入图片描述
第一趟处理完毕，基准数46的左边都是小于基准数46的元素，基准数46的右边都是大于基准数46的元素

接着处理第二趟：
分别处理46左边的序列和46右边的序列，我们可以认为46已经找准了它的位置下标了，在最后全部排好序的序列上，它的位置就是现在的位置了。
在这里插入图片描述
现在的操作和二分的思想很相似，又是在走1棵二叉树。
如果树比较平衡，树的层高=log以2为底的n
46左边的序列的处理如下：以32为基准数，进行快速排序

把小于32的都放到32的左边，把大于32的都放到32的右边，此时的32的位置就是最终全部排好序的序列里的位置（3号下标）。
在这里插入图片描述
现在我们处理46右边的序列，以68为基准数

处理完之后，比基准数68小的放在68的左边，比基准数68大的放在68的右边。此时的68的位置就是最终全部排好序的序列里的位置（倒数第2个位置）。
我们继续处理下去：
在这里插入图片描述
38和76就不用处理了，因为只有1个元素了（直接L==R了）38和76的此时的位置就是最终全部排好序的序列里的位置了。
我们处理10-8-7这个序列，以10作为基准数，进行快速排序。
把大于基准数10的放在10的右边，把小于基准数10的放在10的左边
此时的10的位置就是最终全部排好序的序列里的位置。
在这里插入图片描述
然后我们处理53-65，53为基准数，进行快速排序，53左边没有数据了，右边只有一个65，直接R= =L了，不用处理

然后我们继续对10的左边序列7-8处理，以7为基准数，进行快速排序，10的右边就不用处理，因为没有元素了，就一个元素10而已
在这里插入图片描述
再处理的话，7左边没有元素，7就相当于确定位置了，7的右边序列只有一个8，也不用处理了(直接R= =L了）

在这里插入图片描述
注意：快速排序算法没有开辟二维的空间，是在原地进行调整的哦！我们画出来的图是按照快排的逻辑一步一步拆解开的，和二分搜索的过程一样。每一个元素现在已经调整好了，整体是有序的了

实际上，对于快速排序来说，用的也是二分的思想，很快，但是有时候也很慢，实际上，在最好的情况下，我们应该是每一次把基准数都放在中间，我们希望最好的结果是基准数左边的序列和基准数右边的序列的数量是差不多的，才能真真正正的二分起来，才能拿到一棵非常良好的平衡树，效率才是最好的。
如果按照我们上述的思想，基准数都跑到最右边了，最后得到的肯定是非常失衡的树了，效率就达不到我们想要快速排序的最好的时间复杂度了。
在这里插入图片描述

一直分割处理，直到最后要处理的序列的个数只剩下1个元素，才结束。

快速排序算法的递归实现

L<R的原因：R从右边找过来，找到2，没有必要把2放到2上面
在这里插入图片描述

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;//快排分割处理函数
int Partation(int arr[], int l, int r)
{//记录基准数int val = arr[l];//一次快排处理  时间：O(n) * O(logn) = O(nlogn) 空间：O(logn) 递归的深度所占用的栈内存while (l < r)//l==r，退出while循环{while (l < r && arr[r] > val)//右边的元素的值大于基准数val{r--;//右边下标往前走}if (l < r)//右边的元素的值小于基准数val{arr[l] = arr[r];//把右边的元素的值放在左边的位置l++;//左边下标往后走}while (l < r && arr[l] < val)//左边的元素的值小于基准数val{l++;//左边下标往后走}if (l < r)//左边的元素的值大于基准数val{arr[r] = arr[l];//把左边的元素的值放在右边的位置r--;//右边下标往前走}}//l == r的位置，就是放基准数的位置arr[l] = val;return l;
}//快排的递归接口
void QuickSort(int arr[], int begin, int end)
{if (begin >= end)//快排递归结束的条件{return;}//在[begin, end]区间的元素做一次快排分割处理int pos = Partation(arr, begin, end);//对基准数的左边和右边的序列，再分别进行快排//我们只考虑水平的方向的一层的代码，递归负责执行垂直的方向QuickSort(arr, begin, pos - 1);QuickSort(arr, pos + 1, end);
}//快速排序
void QuickSort(int arr[], int size)
{return QuickSort(arr, 0, size - 1);
}int main()
{int arr[10];srand(time(NULL));for (int i = 0; i < 10; i++){arr[i] = rand() % 100 + 1;}for (int v : arr){cout << v << " ";}cout << endl;QuickSort(arr, 10);for (int v : arr){cout << v << " ";}cout << endl;
}

在这里插入图片描述

快速排序算法的性能分析

快排所操作的次数是二叉树的层数（logn)

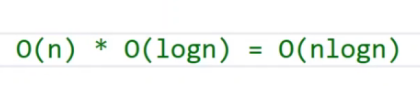
每一次处理，都要拿基准数和左边，右边序列的所有元素进行数据的比较和调整，这个过程是O(n)，每一层是O(n)，总共有logn层，所以，快速排序算法的时间复杂度是O(nlogn)
平均时间复杂度和最好的时间复杂度都是O(nlogn)
在这里插入图片描述
最好的和平均的空间复杂度：
快速排序算法并没有开辟额外的空间，但是是用递归实现的，递归的次数越多，自己调用自己的个数越多，调用1次函数，就开辟1次函数栈帧。
所以，快速排序算法的空间复杂度是看递归的深度，每一次递归代表1次栈帧的开辟，递归的深度越深，开辟的栈内存越大，深度就是二叉树的层数logn
在这里插入图片描述
我们希望快排的时候的基准数尽量放在中间，左边和右边剩余的个数尽量保持一致，这样画出来的二叉树是非常平衡的，不管从根节点到哪个叶子节点，深度几乎是一样的

最坏的时间复杂度和空间复杂度的情况是：
像下图出现，有的根节点到叶子节点的路径非常长，有的根节点到叶子节点的路径比较短，
在这里插入图片描述
假如说，对于1个已经排序好的数据进行快速排序，

对于这样的序列，采用快速排序操作，高不高效？
一上来，选择1作为基准数，然后以此类推下去，没有二叉起来，所以有10个元素，深度就是10，深度是O(n)，即最坏的空间复杂度是O(n)
也就是说，元素有多少个，深度就是多少次
每一次都要拿基准数和剩下的所有元素进行比较，时间复杂度是O(n)
所以，最后的时间复杂度是O(n^2)
在这里插入图片描述
所以，我们希望这个二叉树尽量长成这个样子：
平衡的二叉树

根到叶子节点的高度都是一样的，或者高度差不超过1

不稳定：

对上面序列，我们采用5作为基准数，

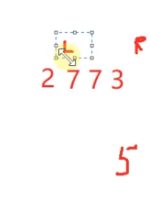
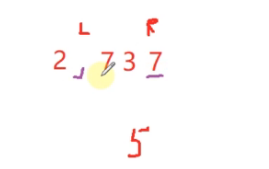
相同值的元素的相对位置发生了改变，所以快速排序算法是不稳定的。
稳定和不稳定，没有说是好还是不好的，主要是看应用场景哦
如果是key-value，key相同的情况下，希望value也依然按照最开始的方法排序，就是要排序是稳定的！没有，就不需要

快速排序算法的优化

在这里插入图片描述
极端情况：对于已经有序的序列，采用快排好不好？不好！时间复杂度是O(n^2)

所以，我们要让快排的基准数理想是放在中间位置。


//快排的递归接口
void QuickSort(int arr[], int begin, int end)
{if (begin >= end)//快排递归结束的条件{return;}//优化一：当[begin, end]序列的元素个数小到指定数量，采用插入排序if (end - begin <= 50){InsertSort(arr, begin, end);//调用插入排序return;}//在[begin, end]区间的元素做一次快排分割处理int pos = Partation(arr, begin, end);//对基准数的左边和右边的序列，再分别进行快排//我们只考虑水平的方向的一层的代码，递归负责执行垂直的方向QuickSort(arr, begin, pos - 1);QuickSort(arr, pos + 1, end);
}

优化2：
如果我们选择的是第一个基准数，这个基准数可能是最大的或者是最小的，这样就可能称为失衡的树了
我们希望选择合适的基准数，尽量跑到中间位置，让二叉树的深度到达logn
，趋于平衡树
在这里插入图片描述

三数取中：取这3个下标对应的元素的大小中，排在中间大的那个元素。

取的是数值在中间的数：38，而不是直接取middle下标的元素
38成为基准数，相对来说，就得到一个良好的快排分割的结果
在这里插入图片描述

在这里插入图片描述
对于这个已经有序的序列，采用三数取中
取的数字1,10，5
5是中间大的数字
然后把5和1交换
让5在首位置，1在中间位置，以5为基准数，进行快速排序

#include <iostream>
#include <stdlib.h>
#include <time.h>
using namespace std;//快排分割处理函数
int Partation(int arr[], int l, int r)
{//选择基准数的优化：“三数取中”法  arr[l]  arr[r]  arr[(l+r)/2]  //记录基准数int val = arr[l];//一次快排处理  时间：O(n) * O(logn) = O(nlogn) 空间：O(logn) 递归的深度所占用的栈内存while (l < r)//l==r，退出while循环{while (l < r && arr[r] > val)//右边的元素的值大于基准数val{r--;//右边下标往前走}if (l < r)//右边的元素的值小于基准数val{arr[l] = arr[r];//把右边的元素的值放在左边的位置l++;//左边下标往后走}while (l < r && arr[l] < val)//左边的元素的值小于基准数val{l++;//左边下标往后走}if (l < r)//左边的元素的值大于基准数val{arr[r] = arr[l];//把左边的元素的值放在右边的位置r--;//右边下标往前走}}//l == r的位置，就是放基准数的位置arr[l] = val;return l;
}//快排的递归接口
void QuickSort(int arr[], int begin, int end)
{if (begin >= end)//快排递归结束的条件{return;}//优化一：当[begin, end]序列的元素个数小到指定数量，采用插入排序//if (end - begin <= 50)//{// InsertSort(arr, begin, end);//调用插入排序//return;//}//在[begin, end]区间的元素做一次快排分割处理int pos = Partation(arr, begin, end);//对基准数的左边和右边的序列，再分别进行快排//我们只考虑水平的方向的一层的代码，递归负责执行垂直的方向QuickSort(arr, begin, pos - 1);QuickSort(arr, pos + 1, end);
}//快速排序
void QuickSort(int arr[], int size)
{return QuickSort(arr, 0, size - 1);
}int main()
{int arr[10];srand(time(NULL));for (int i = 0; i < 10; i++){arr[i] = rand() % 100 + 1;}for (int v : arr){cout << v << " ";}cout << endl;QuickSort(arr, 10);for (int v : arr){cout << v << " ";}cout << endl;
}

快速排序：数据越乱越好，数据越乱，快排的效率越高。
如果序列是趋于有序，或者选择的第一个数（基准数）是最大的或者是最小的，比较大的或者比较小的，效率就慢慢降低了

快速排序算法非递归实现

1、利用一个栈，把右边终点入栈，然后把左边起点入栈，因为栈的特点是先进后出，后进先出
2、然后进入while循环，条件是栈不为空
3、然后依次出栈2个元素，就是一次快排划分的起点和终点下标
4、一次快排划分后，返回基准数的下标，然后进行左右判断，判断结果是否大于1，是否需要继续入栈
5、直到栈为空，快排完成！！！

#include<iostream>
#include<stack>using namespace std;int OneQuick(int* arr, int left, int right)//一次快排划分函数
{int tmp = arr[left];while (left < right){//从right向前找比基准数据小的while (left < right && arr[right] >= tmp){right--;}arr[left] = arr[right];//从left向后找比基准数据大的while (left < right && arr[left] <= tmp){left++;}arr[right] = arr[left];}arr[left] = tmp;return left;
}void Quick(int* arr, int left, int right)
{stack<int> st;//记录待排序序列的下标st.push(right);//右边终点入栈st.push(left);//左边起点入栈while (!st.empty()){//利用一个栈，把右边终点入栈，然后把左边起点入栈，因为栈的特点是先进后出，后进先出//然后进入while循环，条件是栈不为空//然后出栈2个元素，就是一次快排划分的起点和终点下标//一次快排划分后，返回基准数的下标，然后进行左右判断，判断结果是否大于1，是否需要继续入栈//直到栈为空，快排完成！！！int start, end;start = st.top();//先出栈的就是起点st.pop();end = st.top();//后出栈的就是终点st.pop();int mid = OneQuick(arr, start, end);//快排划分if (mid - start > 1){st.push(mid-1);st.push(start);}if (end - mid > 1){st.push(end);st.push(mid+1);}}
}int main()
{int arr[] = { 15,23,11,78,4,56,2,4,98 };int n = sizeof(arr) / sizeof(arr[0]);for (int i = 0; i < n; ++i){cout << arr[i] << " ";}cout << endl;Quick(arr, 0, n - 1);for (int i = 0; i < n; ++i){cout << arr[i] << " ";}cout << endl;return 0;
}