1.最小生成树原理

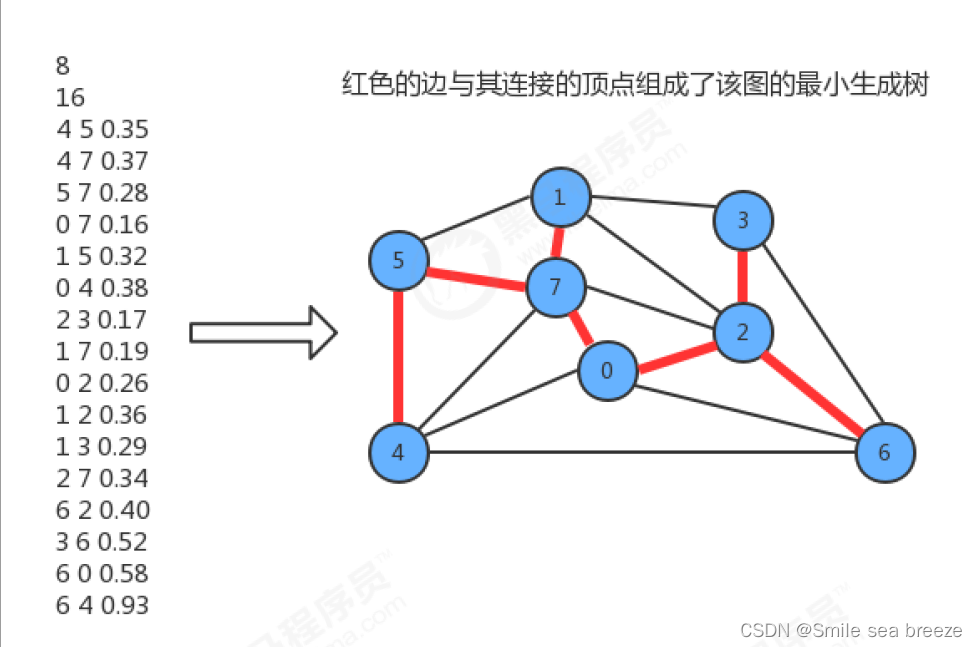
之前学习的加权图，我们发现它的边关联了一个权重，那么我们就可以根据这个权重解决最小成本问题，但如何才能找到最小成本对应的顶点和边呢？最小生成树相关算法可以解决。
定义：
图的生成树是它的一棵含有其所有顶点的无环连通子图，一副加权无向图的最小生成树它的一棵权值(树中所有边的权重之和)最小的生成树

约定：
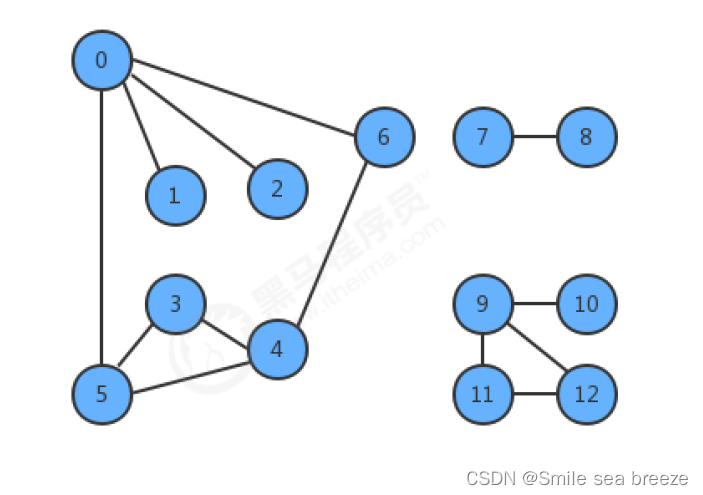
只考虑连通图。最小生成树的定义说明它只能存在于连通图中，如果图不是连通的，那么分别计算每个连通图子图的最小生成树，合并到一起称为最小生成森林。

所有边的权重都各不相同。如果不同的边权重可以相同，那么一副图的最小生成树就可能不唯一了，虽然我们的算法可以处理这种情况，但为了好理解，我们约定所有边的权重都各不相同。

1.1 树的性质

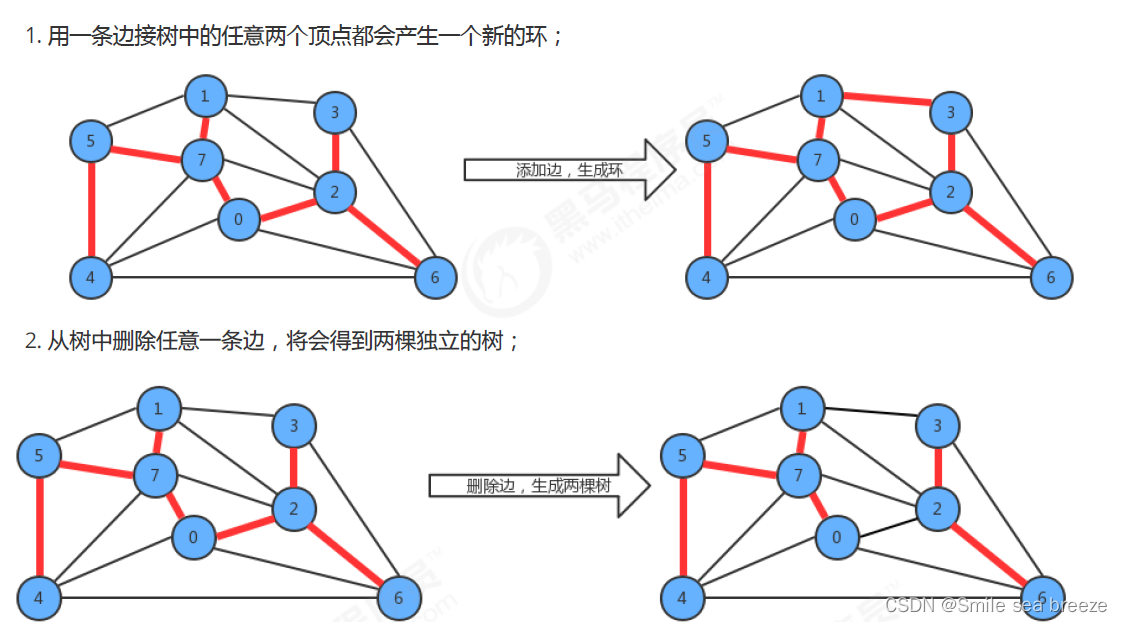
在这里插入图片描述

1.2 切分定理

要从一副连通图中找出该图的最小生成树，需要通过切分定理完成。
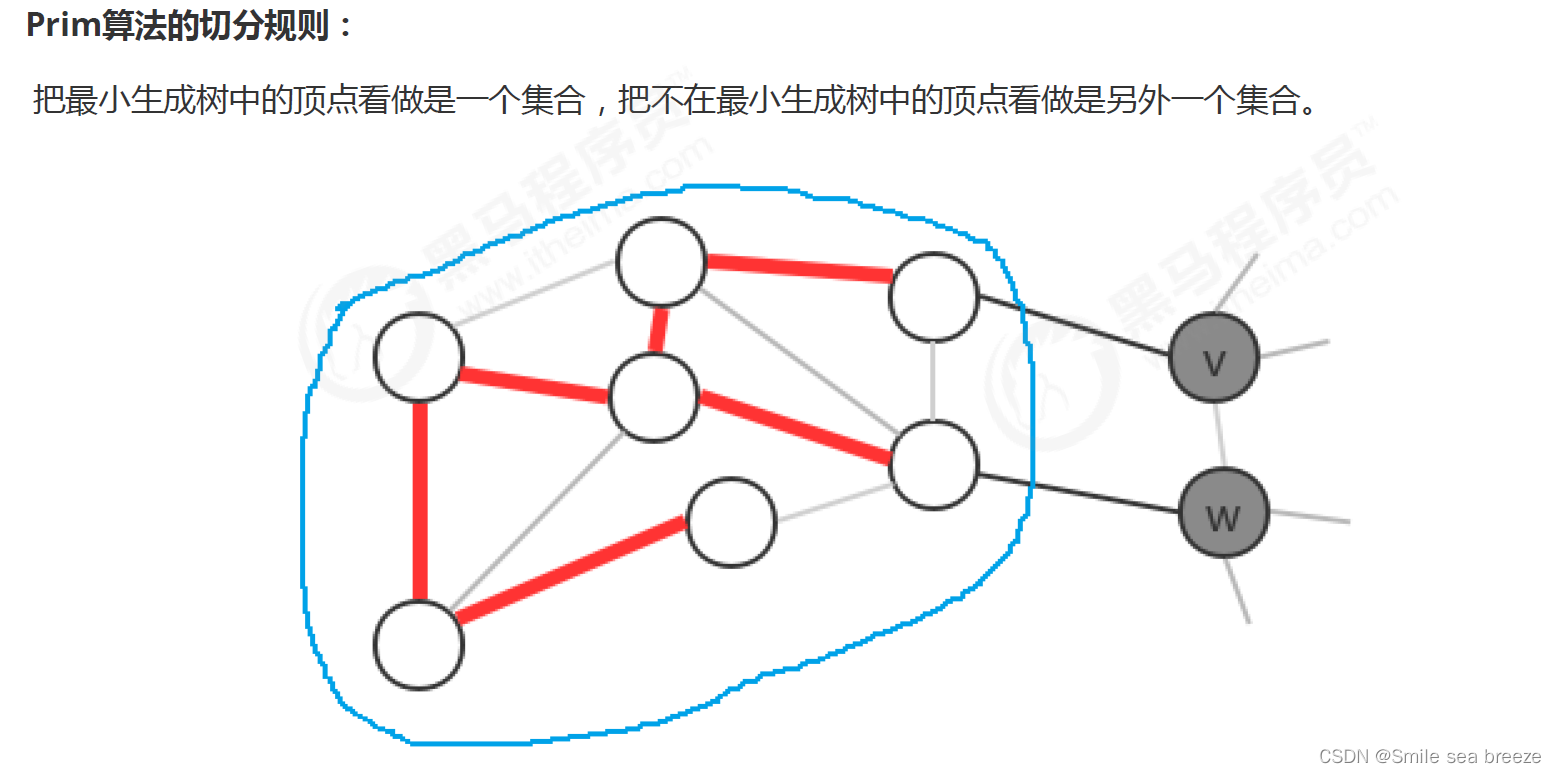
切分：
将图的所有顶点按照某些规则分为两个非空且没有交集的集合。
横切边：
连接两个属于不同集合的顶点的边称之为横切边。
例如我们将图中的顶点切分为两个集合，灰色顶点属于一个集合，白色顶点属于另外一个集合，那么效果如下：
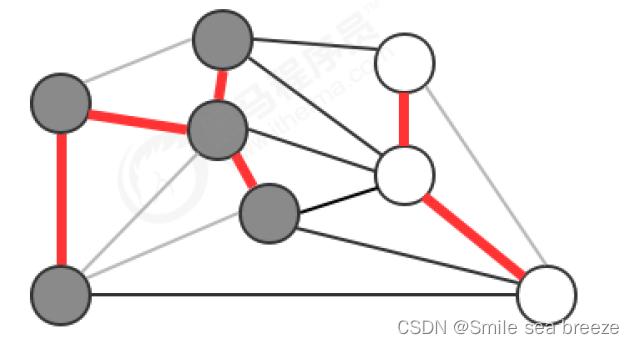
在这里插入图片描述
切分定理：

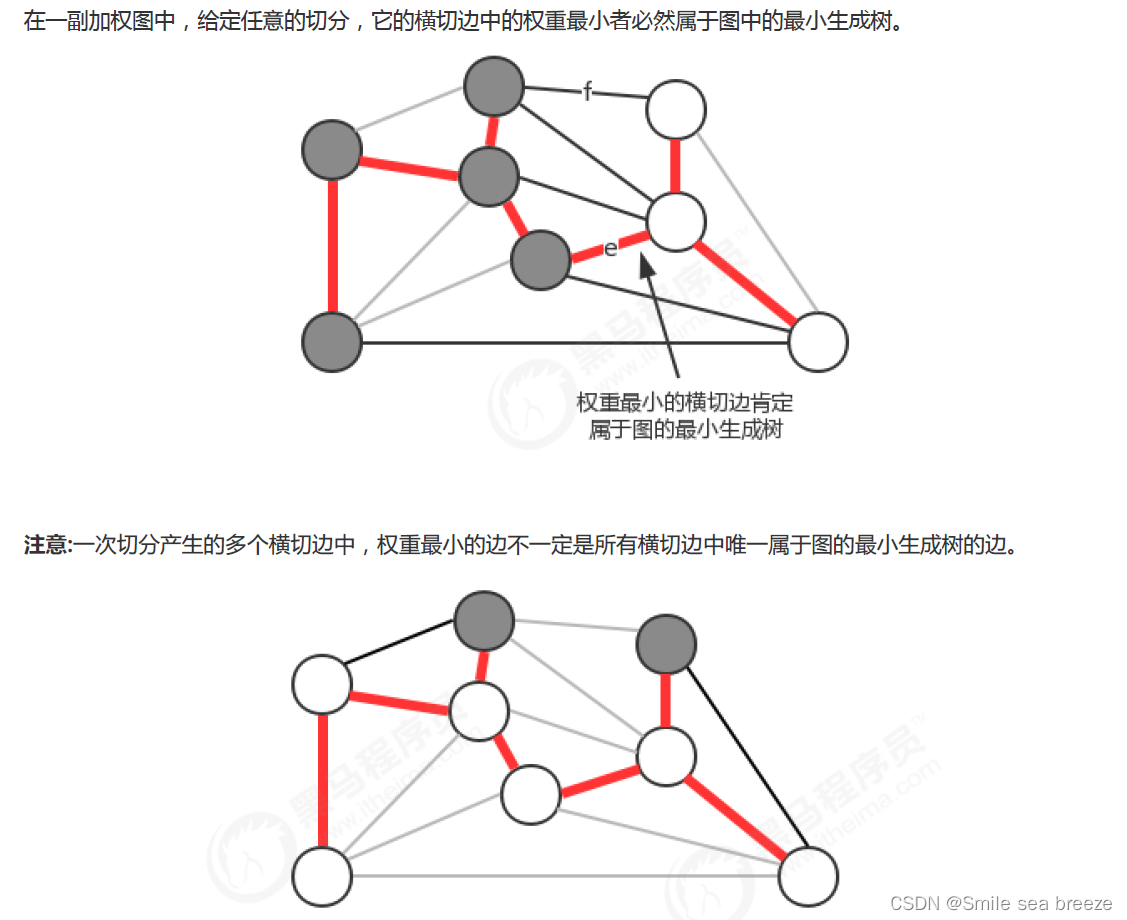
2.贪心算法

贪心算法是计算图的最小生成树的基础算法，它的基本原理就是切分定理，使用切分定理找到最小生成树的一条边，不断的重复直到找到最小生成树的所有边。如果图有V个顶点，那么需要找到V-1条边，就可以表示该图的最小生成树。
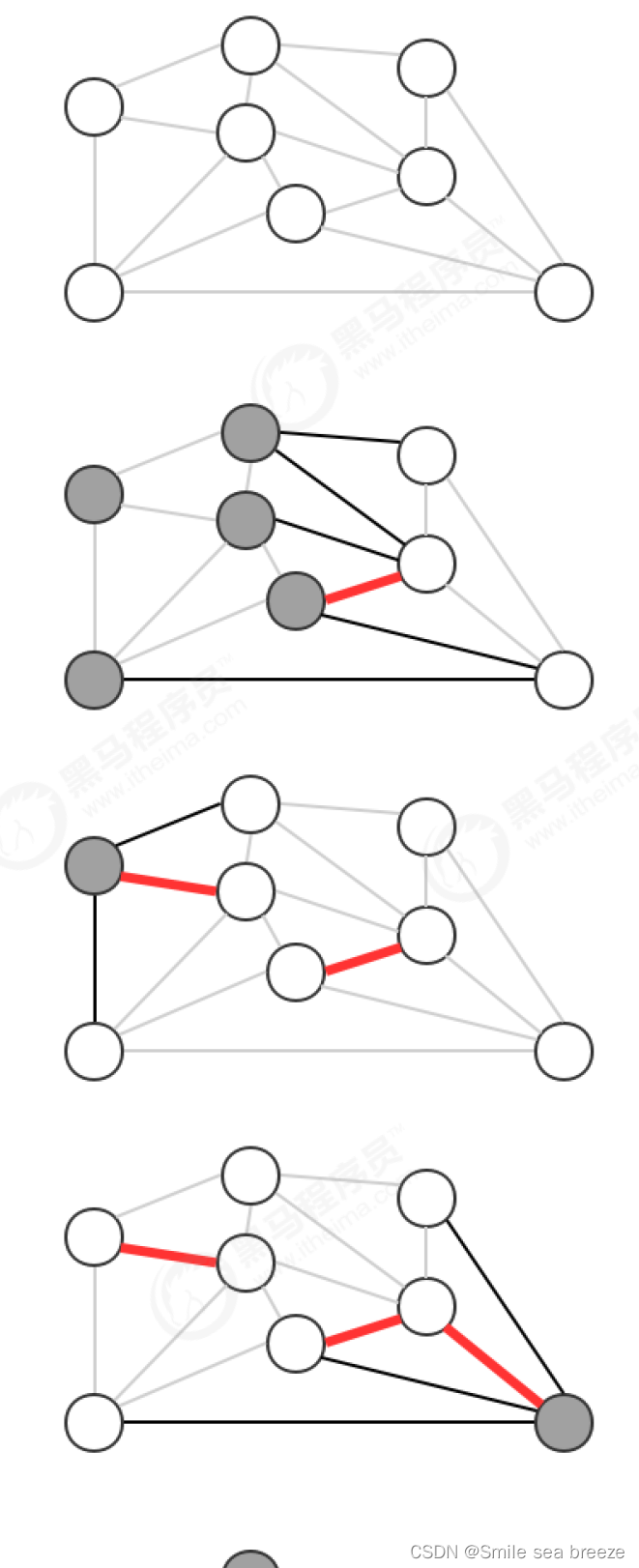
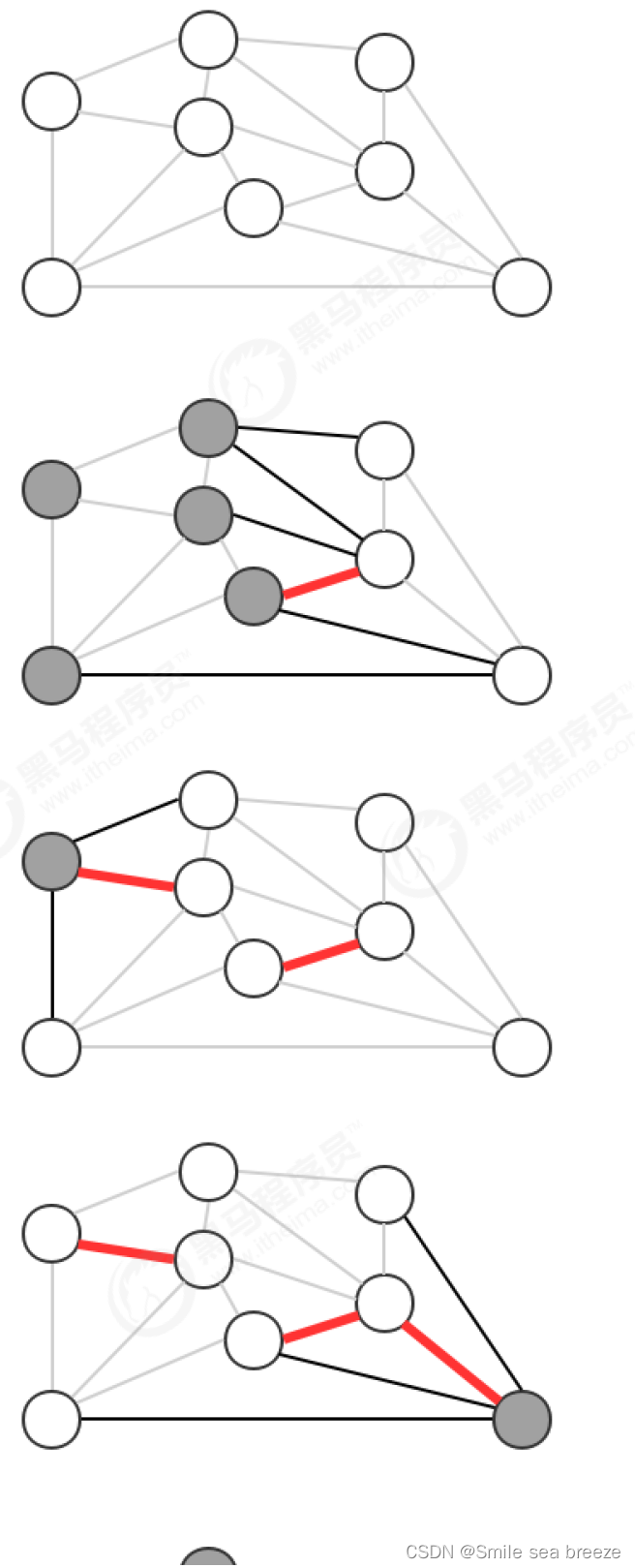
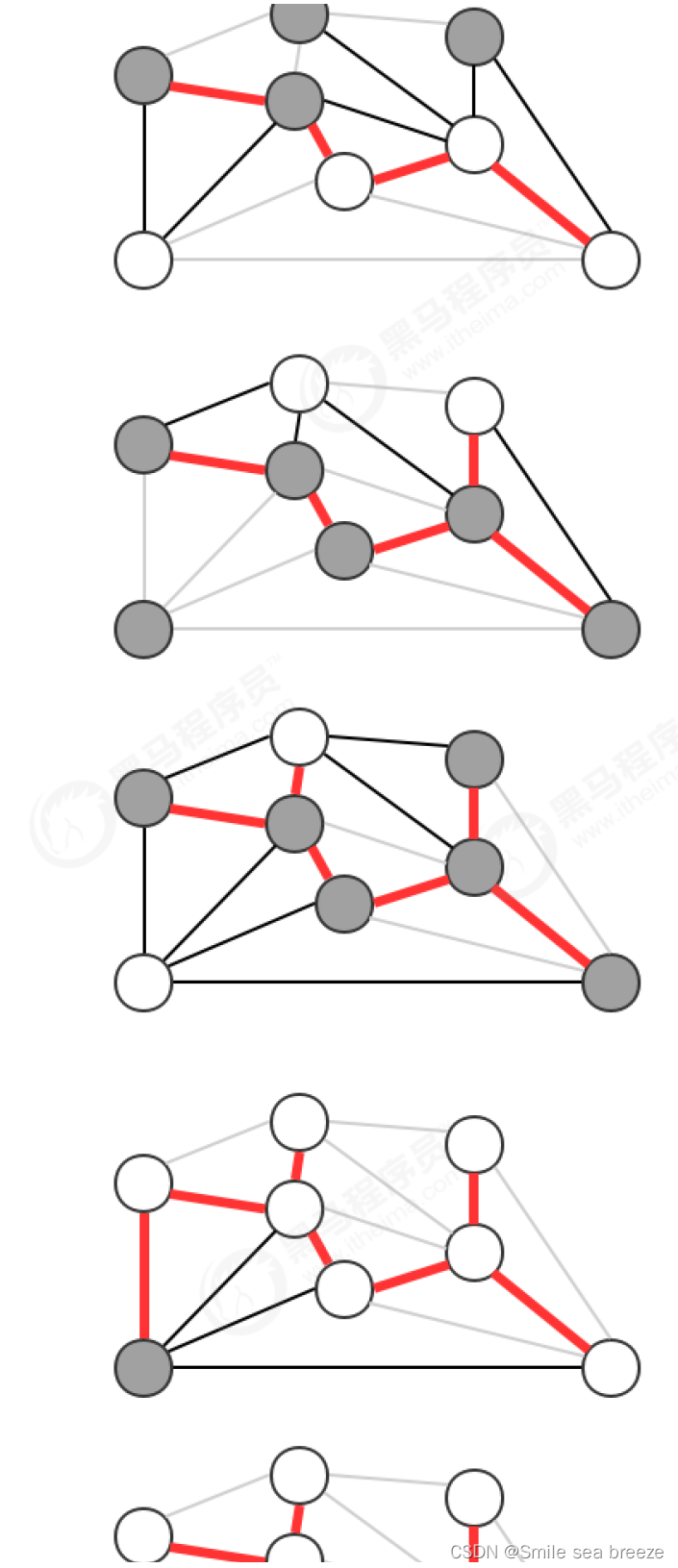
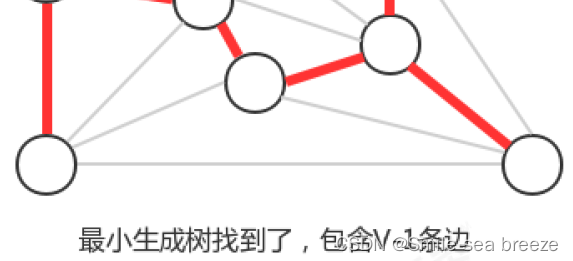
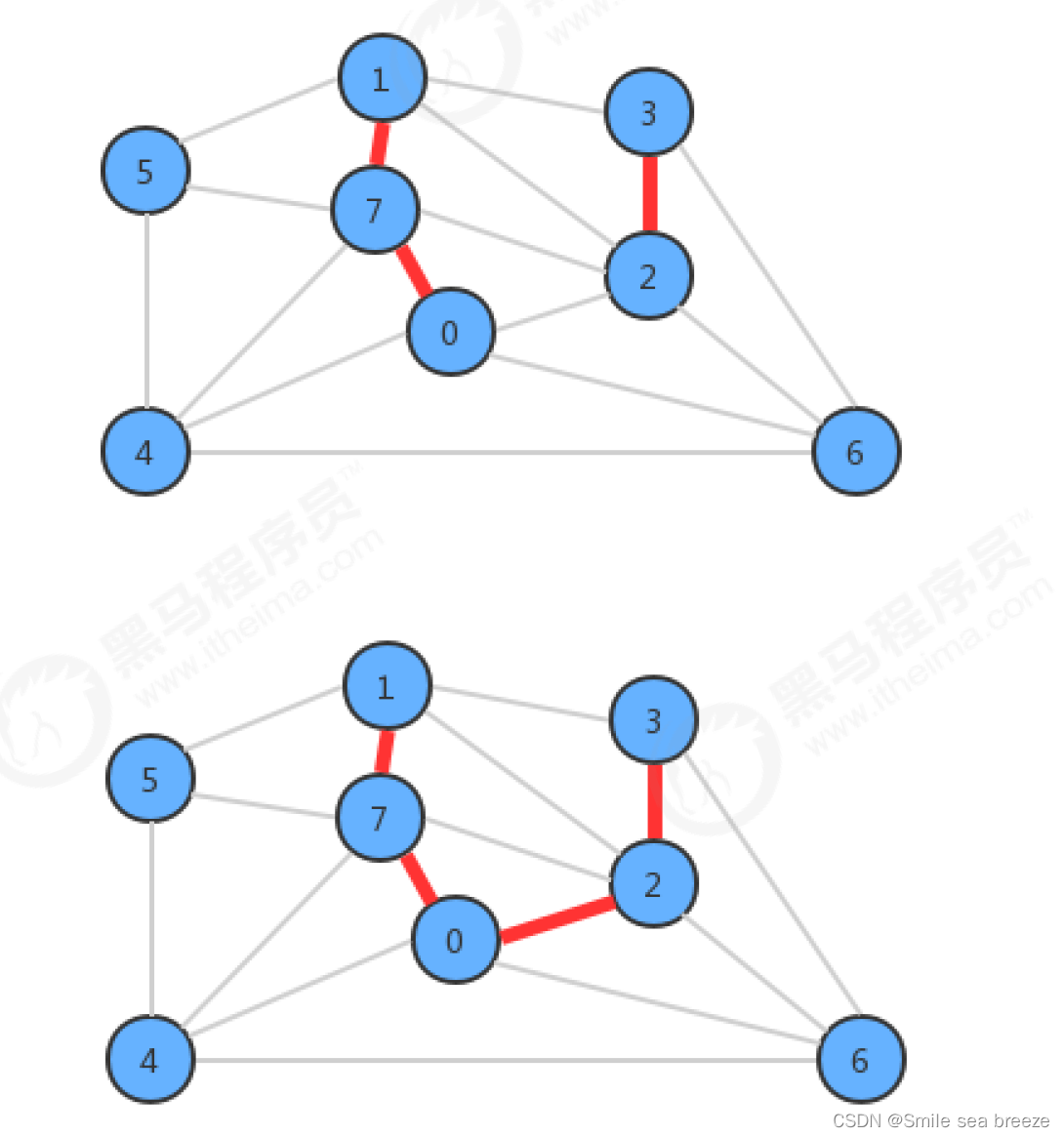
在这里插入图片描述

在这里插入图片描述

3.Prim算法

我们学习第一种计算最小生成树的方法叫Prim算法，它的每一步都会为一棵生成中的树添加一条边。一开始这棵树只有一个顶点，然后会向它添加V-1条边，每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中。

3.1 API设计

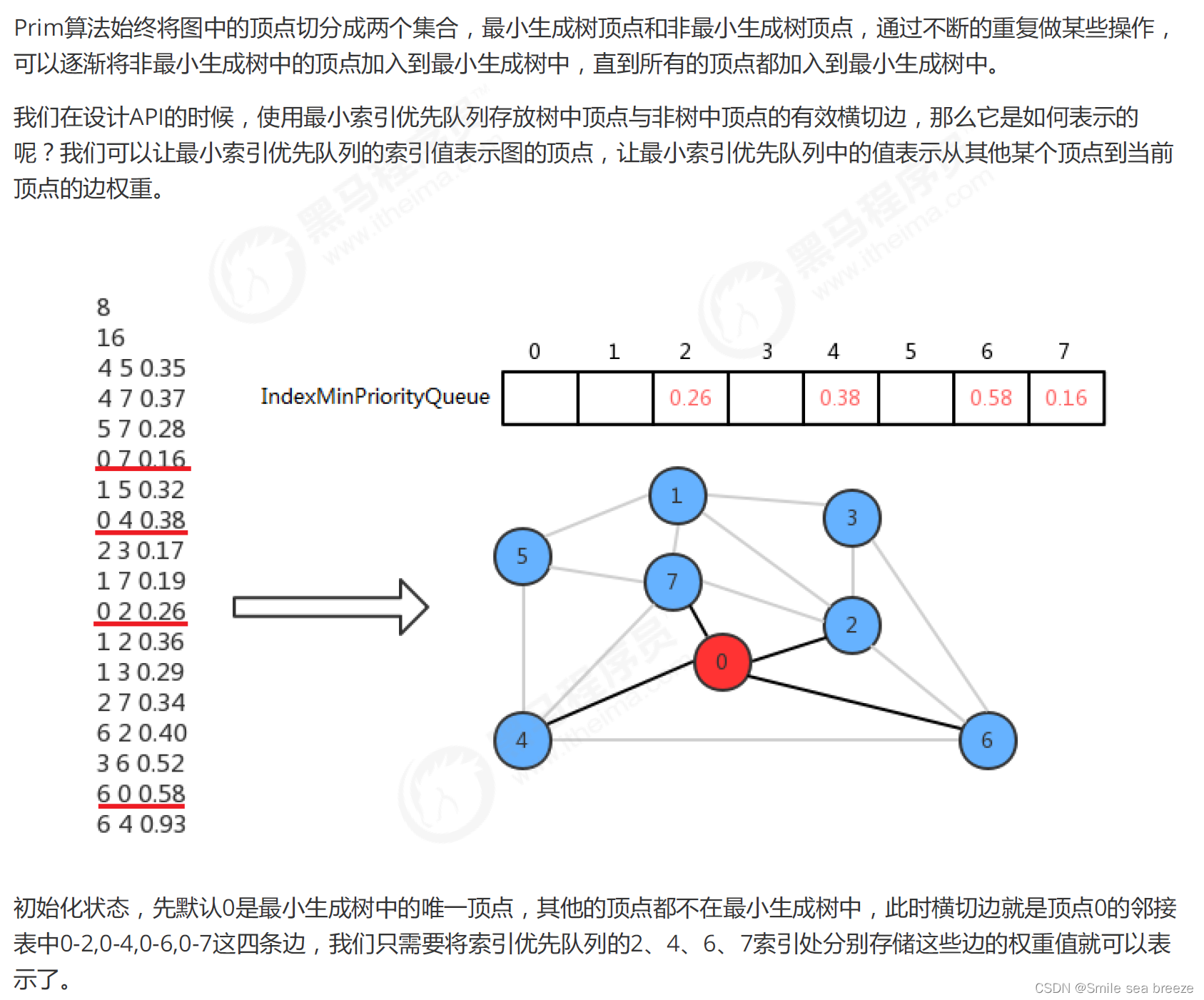
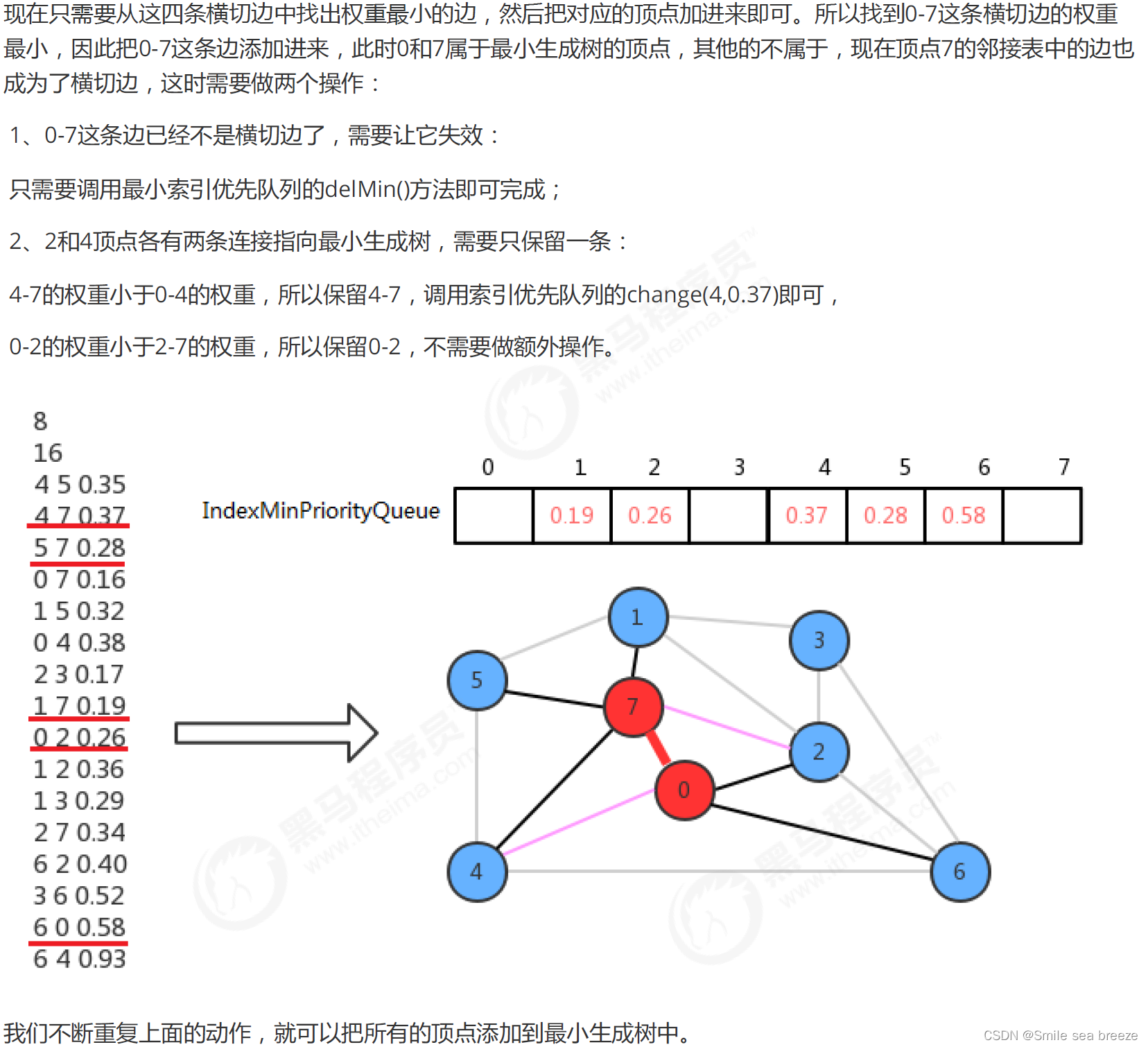
在这里插入图片描述

3.2 代码实现

public class PrimMST {//索引代表顶点，值表示当前顶点和最小生成树之间的最短边private Edge[] edgeTo;//索引代表顶点，值表示当前顶点和最小生成树之间的最短边的权重private double[] distTo;//索引代表顶点，如果当前顶点已经在树中，则值为true，否则为falseprivate boolean[] marked;//存放树中顶点与非树中顶点之间的有效横切边private IndexMinPriorityQueue<Double> pq;//根据一副加权无向图，创建最小生成树计算对象public PrimMST(EdgeWeightedGraph G) {//创建一个和图的顶点数一样大小的Edge数组，表示边this.edgeTo = new Edge[G.V()];//创建一个和图的顶点数一样大小的double数组，表示权重，并且初始化数组中的内容为无穷大，无穷大即表示不存在这样的边this.distTo = new double[G.V()];for (int i = 0; i < distTo.length; i++) {distTo[i] = Double.POSITIVE_INFINITY;}//创建一个和图的顶点数一样大小的boolean数组，表示当前顶点是否已经在树中this.marked = new boolean[G.V()];//创建一个和图的顶点数一样大小的索引优先队列，存储有效横切边this.pq = new IndexMinPriorityQueue<>(G.V());//默认让顶点0进入树中，但0顶点目前没有与树中其他的顶点相连接，因此初始化distTo[0]=0.0distTo[0] = 0.0;//使用顶点0和权重0初始化pqpq.insert(0, 0.0);//遍历有效边队列while (!pq.isEmpty()) {//找到权重最小的横切边对应的顶点，加入到最小生成树中visit(G, pq.delMin());}}//将顶点v添加到最小生成树中，并且更新数据private void visit(EdgeWeightedGraph G, int v) {//把顶点v添加到树中marked[v] = true;//遍历顶点v的邻接表,得到每一条边Edge e,for (Edge e : G.adj(v)) {//边e的一个顶点是v，找到另外一个顶点w；int w = e.other(v);//检测是否已经在树中，如果在，则继续下一次循环，如果不在，则需要修正当前顶点w距离最小生成树的最小边edgeTo[w]以及它的权重distTo[w]，还有有效横切边也需要修正if (marked[w]) {continue;}//如果v-w边e的权重比目前distTo[w]权重小，则需要修正数据if (e.weight() < distTo[w]) {//把顶点w距离最小生成树的边修改为eedgeTo[w] = e;//把顶点w距离最小生成树的边的权重修改为e.weight()distTo[w] = e.weight();//如果pq中存储的有效横切边已经包含了w顶点，则需要修正最小索引优先队列w索引关联的权重值if (pq.contains(w)) {pq.changeItem(w, e.weight());} else {//如果pq中存储的有效横切边不包含w顶点，则需要向最小索引优先队列中添加v-w和其权重值pq.insert(w, e.weight());}}}}//获取最小生成树的所有边public Queue<Edge> edges() {//创建队列Queue<Edge> edges = new Queue<>();//遍历edgeTo数组，找到每一条边，添加到队列中for (int i = 0; i < marked.length; i++) {if (edgeTo[i]!=null){edges.enqueue(edgeTo[i]);}}return edges;}}//测试代码public class PrimTest {public static void main(String[] args) throws Exception {//创建输入流BufferedReader reader = new BufferedReader(newInputStreamReader(PrimTest.class.getClassLoader().getResourceAsStream("min_create_tree_test.txt")));//读取顶点数目，初始化EdgeWeightedGraph图int number = Integer.parseInt(reader.readLine());EdgeWeightedGraph G = new EdgeWeightedGraph(number);//读取边的数目int edgeNumber = Integer.parseInt(reader.readLine());//循环读取每一条边，并调用addEdge方法for (int i = 0; i < edgeNumber; i++) {String line = reader.readLine();int v = Integer.parseInt(line.split(" ")[0]);int w = Integer.parseInt(line.split(" ")[1]);double weight = Double.parseDouble(line.split(" ")[2]);G.addEdge(new Edge(v, w, weight));}//构建PrimMST对象PrimMST mst = new PrimMST(G);//获取最小生成树的边Queue<Edge> edges = mst.edges();//打印输出for (Edge edge : edges) {if (edge!=null){System.out.println(edge.either() + "-" + edge.other(edge.either()) + "::" +edge.weight());}}}
}

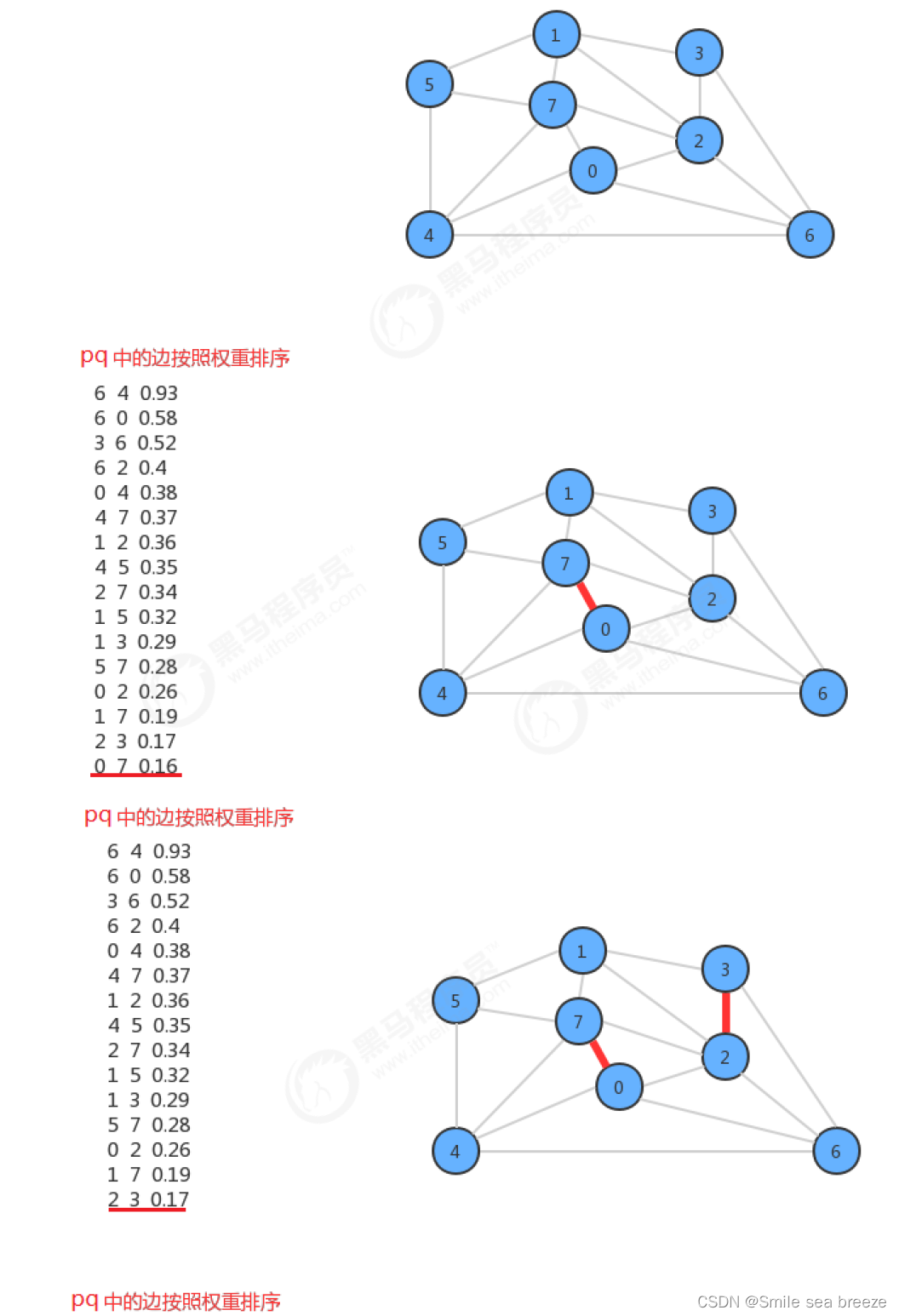
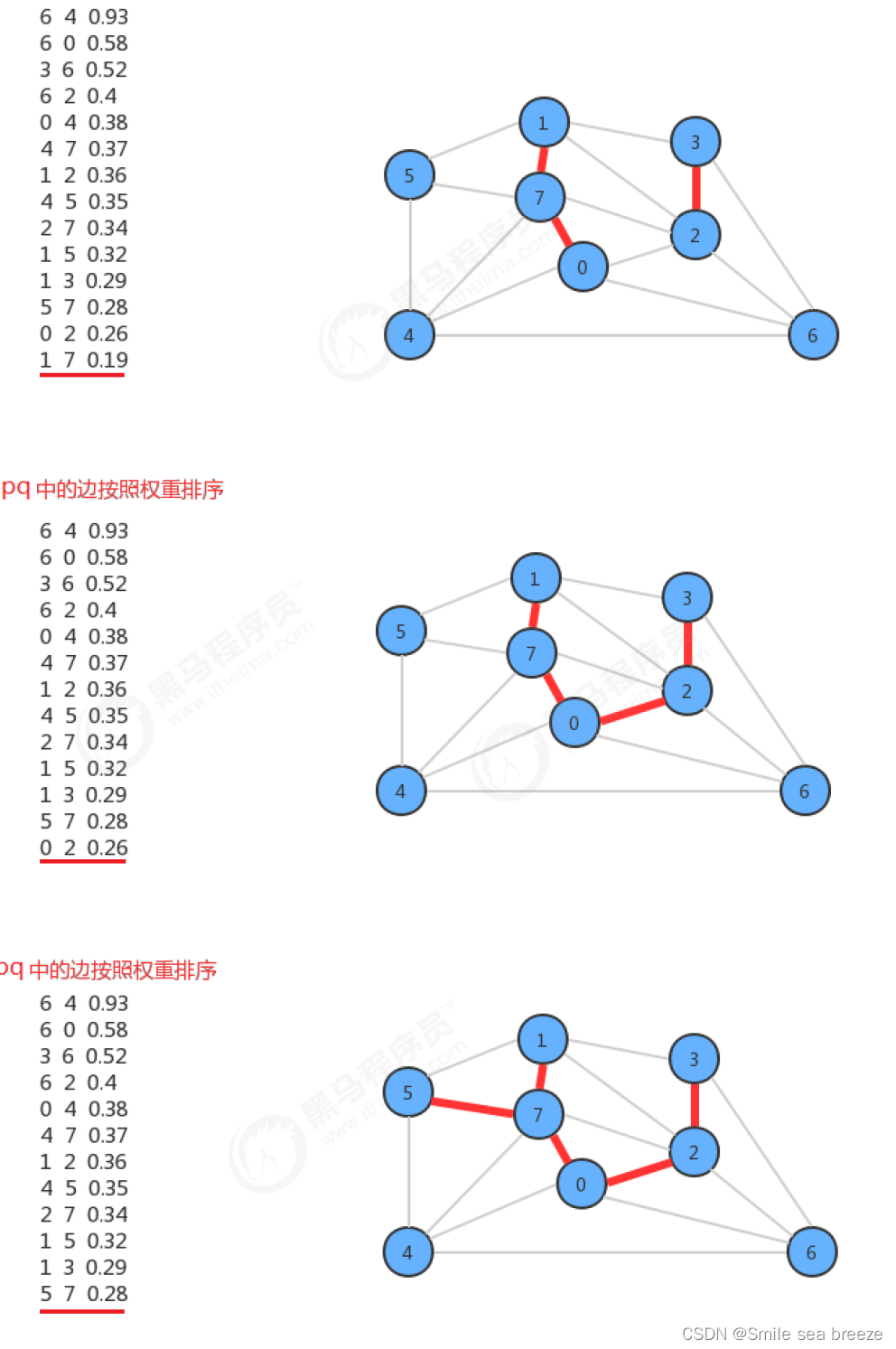
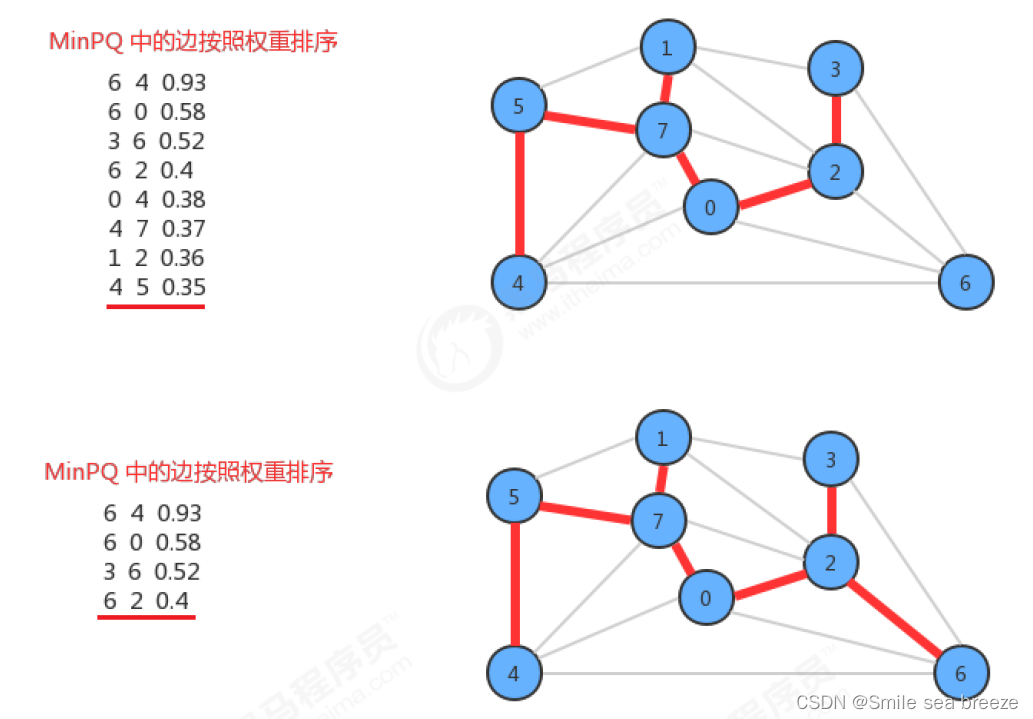
4.kruskal算法

kruskal算法是计算一副加权无向图的最小生成树的另外一种算法，它的主要思想是按照边的权重(从小到大)处理它们，将边加入最小生成树中，加入的边不会与已经加入最小生成树的边构成环，直到树中含有V-1条边为止。
kruskal算法和prim算法的区别：
Prim算法是一条边一条边的构造最小生成树，每一步都为一棵树添加一条边。
kruskal算法构造最小生成树的时候也是一条边一条边地构造，但它的切分规则是不一样的。它每一次寻找的边会连接一片森林中的两棵树。如果一副加权无向图由V个顶点组成，初始化情况下每个顶点都构成一棵独立的树，则V个顶点对应V棵树，组成一片森林，kruskal算法每一次处理都会将两棵树合并为一棵树，直到整个森林中只剩一棵树为止。

4.1 API设计

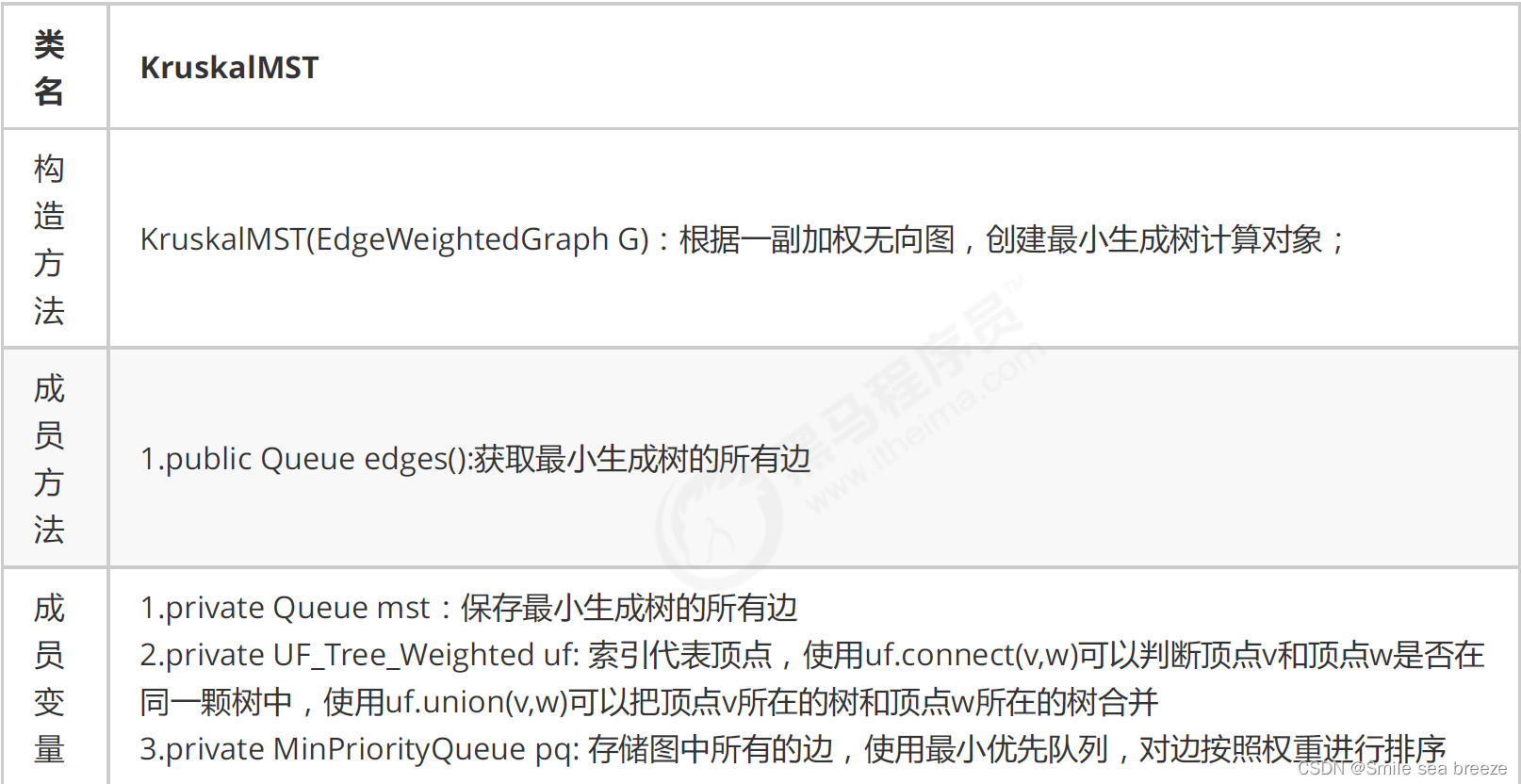
在这里插入图片描述

在设计API的时候，使用了一个MinPriorityQueue pq存储图中所有的边，每次使用pq.delMin()取出权重最小的边，并得到该边关联的两个顶点v和w，通过uf.connect(v,w)判断v和w是否已经连通，如果连通，则证明这两个顶点在同一棵树中，那么就不能再把这条边添加到最小生成树中，因为在一棵树的任意两个顶点上添加一条边，都会形成环，而最小生成树不能有环的存在，如果不连通，则通过uf.connect(v,w)把顶点v所在的树和顶点w所在的树
合并成一棵树，并把这条边加入到mst队列中，这样如果把所有的边处理完，最终mst中存储的就是最小生树的所有边。

4.2 代码实现

public class KruskalMST {//保存最小生成树的所有边private Queue<Edge> mst;//索引代表顶点，使用uf.connect(v,w)可以判断顶点v和顶点w是否在同一颗树中，使用uf.union(v,w)可以把顶点v所在的树和顶点w所在的树合并private UF_Tree_Weighted uf;//存储图中所有的边，使用最小优先队列，对边按照权重进行排序private MinPriorityQueue<Edge> pq;//根据一副加权无向图，创建最小生成树计算对象public KruskalMST(EdgeWeightedGraph G) {//初始化mst队列this.mst = new Queue<Edge>();//初始化并查集对象uf,容量和图的顶点数相同this.uf = new UF_Tree_Weighted(G.V());//初始化最小优先队列pq，容量比图的边的数量大1，并把图中所有的边放入pq中this.pq = new MinPriorityQueue<>(G.E()+1);for (Edge edge : G.edges()) {pq.insert(edge);}//如果优先队列pq不为空，也就是还有边未处理，并且mst中的边还不到V-1条，继续遍历while (!pq.isEmpty() && mst.size() < G.V() - 1) {//取出pq中权重最小的边eEdge e = pq.delMin();//获取边e的两个顶点v和wint v = e.either();int w = e.other(v);/*通过uf.connect(v,w)判断v和w是否已经连通，如果连通:则证明这两个顶点在同一棵树中，那么就不能再把这条边添加到最小生成树中，因为在一棵树的任意两个顶点上添加一条边，都会形成环，而最小生成树不能有环的存在;如果不连通:则通过uf.connect(v,w)把顶点v所在的树和顶点w所在的树合并成一棵树,并把这条边加入到mst队列中*/if (uf.connected(v,w)){continue;}uf.union(v,w);mst.enqueue(e);}}//获取最小生成树的所有边public Queue<Edge> edges() {return mst;}}//测试代码public class KruskalTest {public static void main(String[] args) throws Exception {//创建输入流BufferedReader reader = new BufferedReader(newInputStreamReader(KruskalTest.class.getClassLoader().getResourceAsStream("min_create_tree_test.txt")));//读取顶点数目，初始化EdgeWeightedGraph图int number = Integer.parseInt(reader.readLine());EdgeWeightedGraph G = new EdgeWeightedGraph(number);//读取边的数目int edgeNumber = Integer.parseInt(reader.readLine());//循环读取每一条边，并调用addEdge方法for (int i = 0; i < edgeNumber; i++) {String line = reader.readLine();int v = Integer.parseInt(line.split(" ")[0]);int w = Integer.parseInt(line.split(" ")[1]);double weight = Double.parseDouble(line.split(" ")[2]);G.addEdge(new Edge(v, w, weight));}//构建PrimMST对象KruskalMST mst = new KruskalMST(G);//获取最小生成树的边Queue<Edge> edges = mst.edges();//打印输出for (Edge edge : edges) {if (edge!=null){System.out.println(edge.either() + "-" + edge.other(edge.either()) + "::" +edge.weight());}}}
}