0x00 二分图

二分图是一个图，它的顶点可以分为两个独立的集合u和v，这样每一条边(u，v)要么从u到v连接一个顶点，要么从v到u连接一个顶点。换句话说，对于每一条边(u，v)，要么u属于u，要么v属于v，或者u属于v，v属于u，也可以说没有边连接同一集合的不同点。

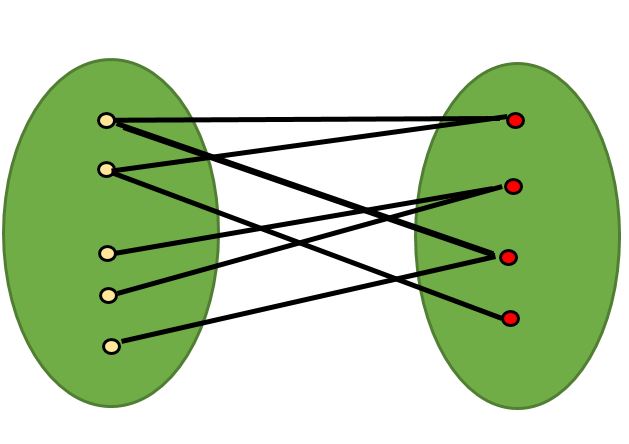
0x01 二分图的判定

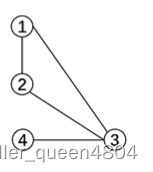
可以通过染色法判定二分图。如果可以通过两种颜色将图染色，使得相同集合中的顶点使用相同的颜色，则为二分图。请注意，仅可以使用两种颜色为偶数顶点个数的图染色。例如，请参见下图。

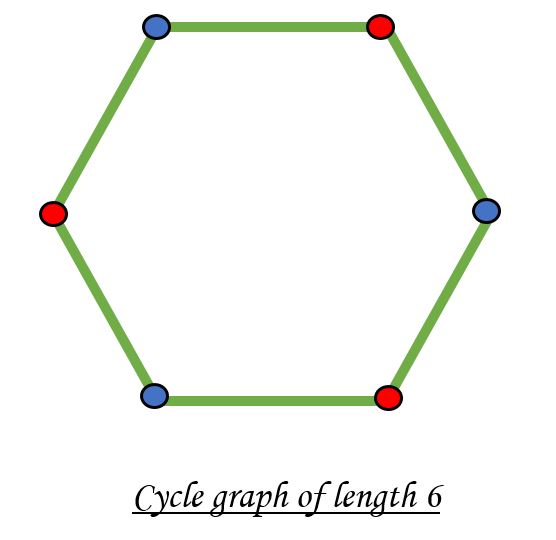
无法使用两种颜色为奇数顶点个数的图染色。

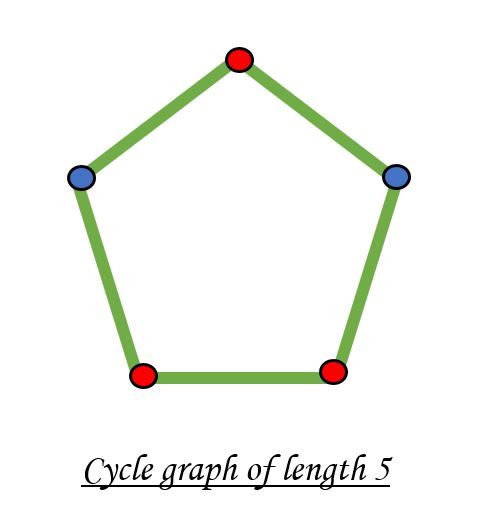
二分图的判定算法主要通过bfs和dfs。首先通过bfs来确定给定的图是否是二分图。

初始点染成红色（放置到集合U中）。
用蓝色给所有邻居涂上颜色（放入第V组）。
用红色给所有邻居的邻居涂上颜色（放入U组）。
这样，将颜色分配给所有顶点，使其满足m路着色问题中m=2的所有约束。
分配颜色时，如果发现一个邻居的颜色与当前顶点的颜色相同，则该图不是二分图。

class Graph():  def __init__(self, V):  self.V = V  self.graph = [[0]*V for _ in range(V)]  self.colorArr = [-1]*self.V def isBipartiteUtil(self, src):  queue = []  queue.append(src)  while queue:  u = queue.pop()  if self.graph[u][u] == 1:  return Falsefor v in range(self.V):   if self.graph[u][v] == 1 and self.colorArr[v] == -1:  self.colorArr[v] = 1 - self.colorArr[u]  queue.append(v)  elif self.graph[u][v] == 1 and self.colorArr[v] == self.colorArr[u]:  return Falsereturn Truedef isBipartite(self): self.colorArr = [-1]*self.V for i in range(self.V): if self.colorArr[i] == -1: if not self.isBipartiteUtil(i): return Falsereturn Trueg = Graph(4)  
g.graph = [[0, 1, 0, 1],  [1, 0, 1, 0],  [0, 1, 0, 1],  [1, 0, 1, 0]]  print "Yes" if g.isBipartite() else "No"

也可以使用dfs来做。

V = 4 
def colorGraph(G, color, pos, c):  color[pos] = c  for i in range(0, V):  if G[pos][i]:  if color[i] == -1:  if not colorGraph(G, color, i, 1-c):return Falseelif color[i] == c:  return False return True def isBipartite(G):  self.colorArr = [-1]*self.V for i in range(self.V): if self.colorArr[i] == -1: if not colorGraph(G, color, pos, 1): return Falsereturn Trueif __name__ == "__main__":  G = [[0, 1, 0, 1],  [1, 0, 1, 0],  [0, 1, 0, 1],  [1, 0, 1, 0]]  if isBipartite(G): print("Yes")  else: print("No")

上述代码中的图的表示是通过邻接矩阵存储的，当然可以通过数组模拟邻接表来处理。关于数组模拟邻接表的知识数组模拟邻接表（超详细！！！）

int n;      // n表示点数
int h[N], e[M], ne[M], idx;     // 邻接表存储图
int color[N];       // 表示每个点的颜色，-1表示为染色，0表示白色，1表示黑色// 参数：u表示当前节点，father表示当前节点的父节点（防止向树根遍历），c表示当前点的颜色
bool dfs(int u, int father, int c)
{color[u] = c;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (color[j] == -1){if (!dfs(j, u, !c)) return false;}else if (color[j] == c) return false;}return true;
}bool check()
{memset(color, -1, sizeof color);bool flag = true;for (int i = 0; i < n; i ++ ){if (color[i] == -1){if (!dfs(i, -1, 0)) return false;}}return true;
}

0x02 二分图的最大匹配

二分图中的匹配是一组边的选择方式，使得一个端点不会对应两条边。最大匹配是最大边数的匹配。在最大匹配中，如果添加了任何边，则不再是匹配。给定的二部图可以有多个最大匹配。

这有什么用？

现实世界中有许多问题可以作为二分匹配来解决。例如，考虑以下问题：

有m个职位申请者和n个职位。每个申请人都有他/她感兴趣的工作子集。每个职位空缺只能接受一个应聘者，一个职位应聘者只能被指定一个职位。找一份工作分配给申请者，以便尽可能多的申请者得到工作。

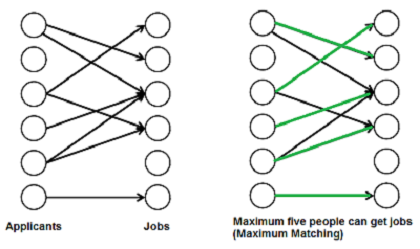
二分图的最大匹配问题实际上可以转化为最大流问题。

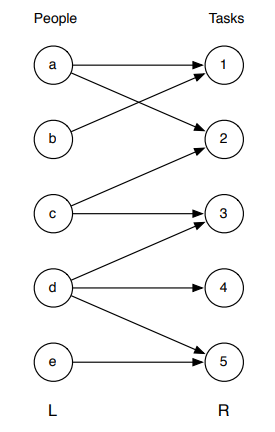
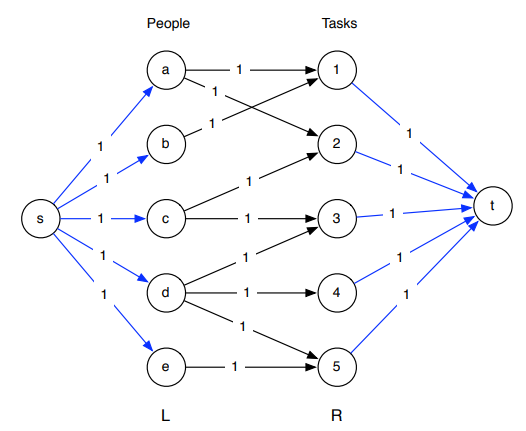
对于二分图来说，每条边的容量相当于0或1，所以我们可以将算法简化。任取一个匹配 $M$ （可以使用空集或一条边），令 $S$ 是非饱和点（尚未匹配的点）的集合。

如果 $S$ 是空集，则 $M$ 已经是最大匹配了。
从 $S$ 中取出一个非饱和点 $u_0$ 作为起点，从此起点走交错路（交替属于 $M$ 和非 $M$ 的边构成的极大无重复点通路或回路） $P$
如果 $P$ 是一个增广路径（ $P$ 的终点也是非饱和点），则令 $M=(M-P)\cup (P-M)$
如果 $P$ 不是增广路径，则从 $S$ 中去掉 $u_0$ ，然后继续递归。

首先解释一下增广路径，这里的增广路径和最大流中有一些区别。从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路径。例如，左图的一条增广路如右图所示（图中的匹配点均用红色标出）：

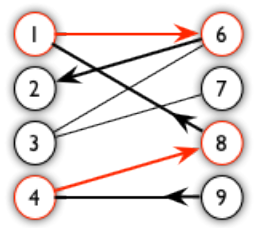
增广路径有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路径的意义是改进匹配。只要把增广路径中的匹配边和非匹配边交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了1条。

int n;      // n表示点数
int h[N], e[M], ne[M], idx;     // 邻接表存储所有边
int match[N];       // 存储每个点当前匹配的点
bool st[N];     // 表示每个点是否已经被遍历过bool find(int x) //判断增广路径
{for (int i = h[x]; ~i; i = ne[i]){int j = e[i];if (!st[j]){st[j] = true;if (match[j] == 0 || find(match[j])){match[j] = x;return true;}}}return false;
}// 求最大匹配数
int res = 0;
for (int i = 0; i < n; i ++ )
{memset(st, false, sizeof st);if (find(i)) res ++ ;
}