Trie树

Trie 树，也叫“字典树”。顾名思义，它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。

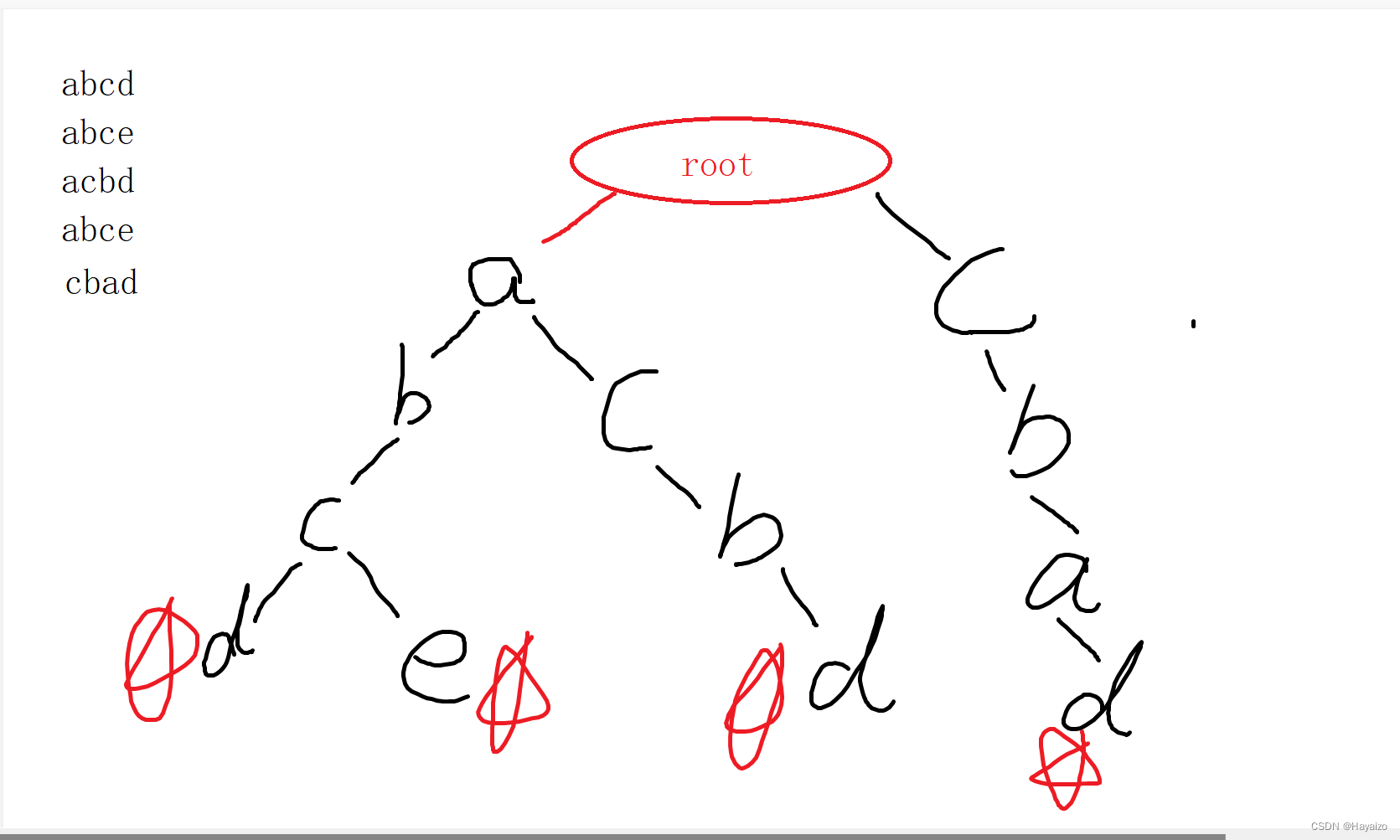
 在每一个单词的结尾需要进行标记，统计个数

现在对上述样例进行模拟

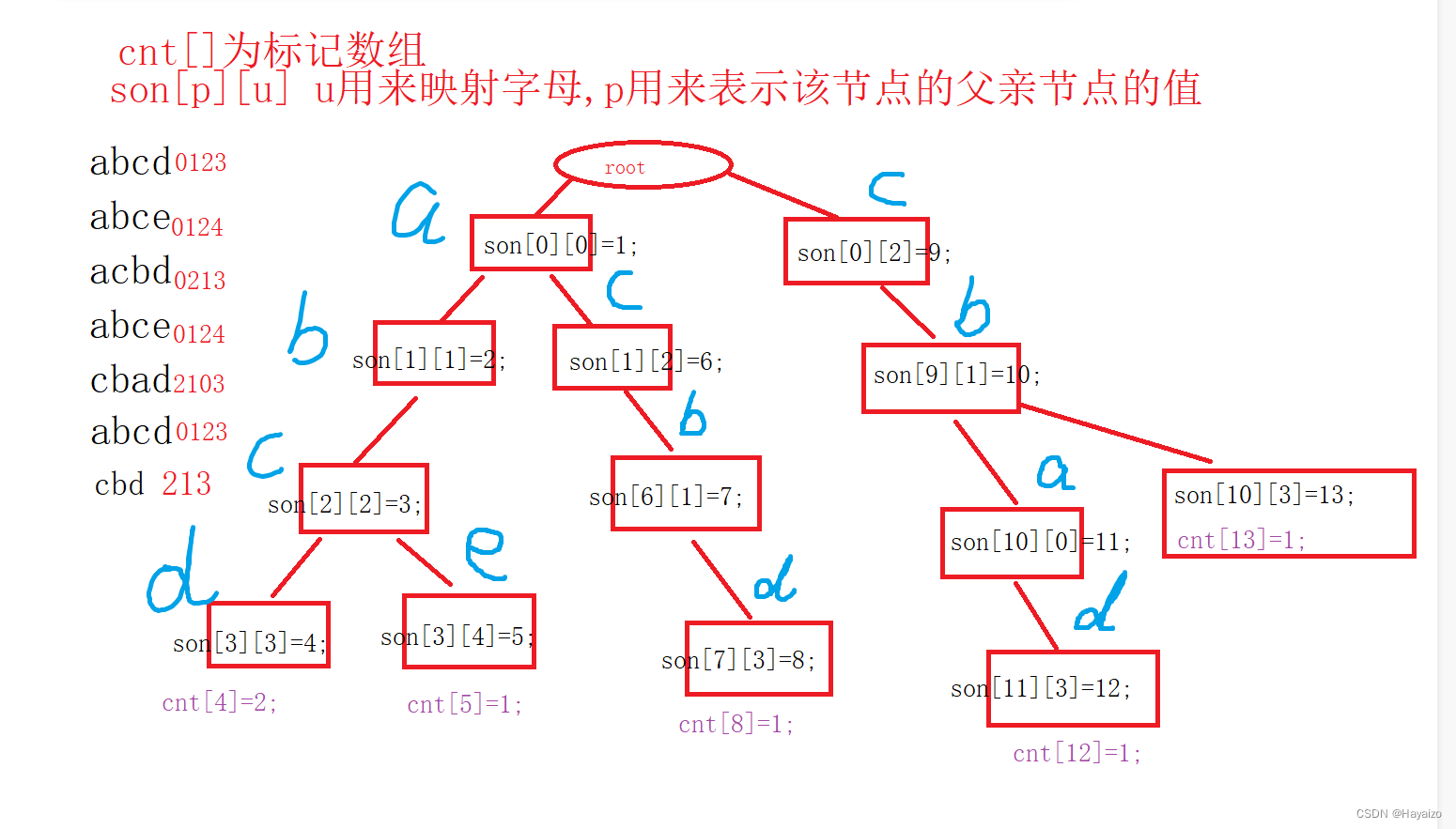
 Trie字符串统计

AC代码：

#include<iostream>
using namespace std;
const int N=100010;
int son[N][26],cnt[N],idx,m;
char str[N];void insert(char* str)
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';//映射if(!son[p][u]) son[p][u]=++idx;p=son[p][u];}cnt[p]++;//计数
}int find(char* str)
{int p=0;for(int i=0;str[i];i++){int u=str[i]-'a';if(!son[p][u]) return 0;p=son[p][u];}return cnt[p];
}int main(void)
{scanf("%d",&m);while(m--){char op[5];scanf("%s %s",op,str);if(op[0]=='I'){insert(str);}else{printf("%d\n",find(str));}}return 0;
}

 并查集

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。常常在使用中以森林来表示。

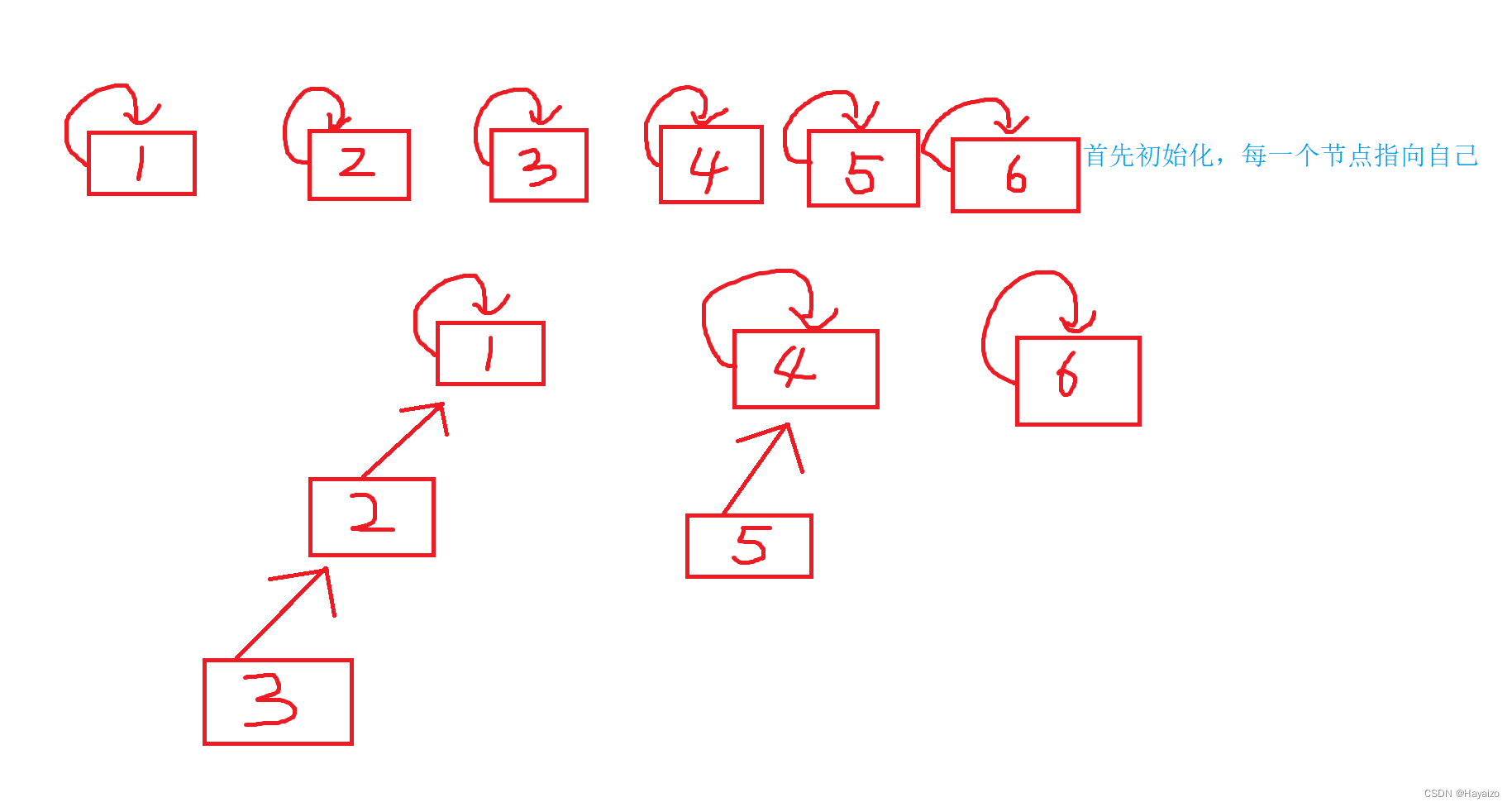
首先创建三个集合，由图可知，每一个点都可以逐级找到自己的祖宗节点，如果祖宗节点相同，那么就是在同一个集合当中，但每一次查找都一个一个找的话效率是十分低效的，因此我们可以采用路径压缩，就是当走完了一个集合之后，我们将这个集合中的所有节点全部指向祖宗节点，那么下一次查找的时间复杂度就是O(1)了，大大提高了查找效率 

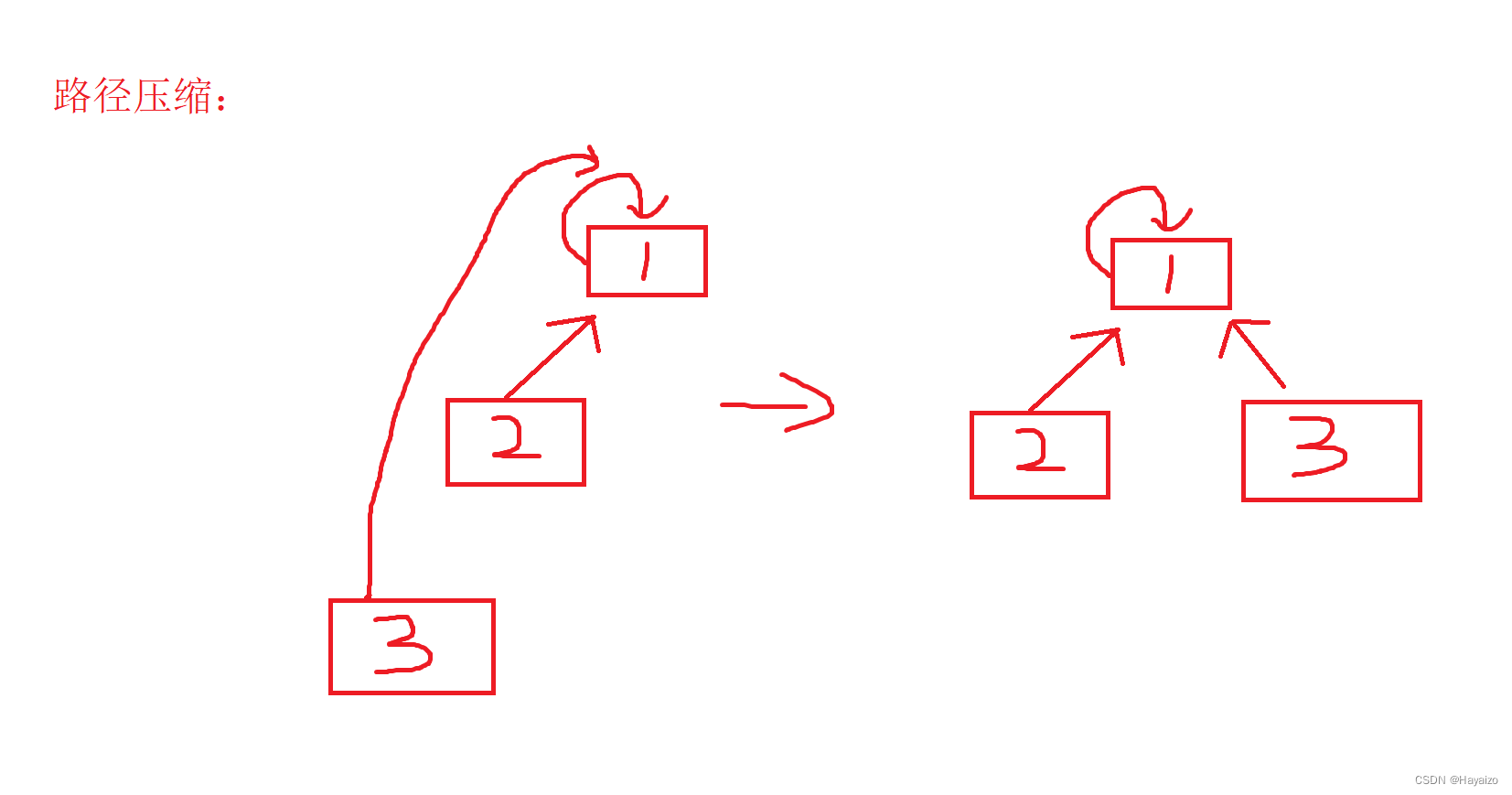
这个操作可以在递归的过程中实现。

int find(int x)
{if(p[x]!=x)p[x]=find(p[x]);return p[x];
}

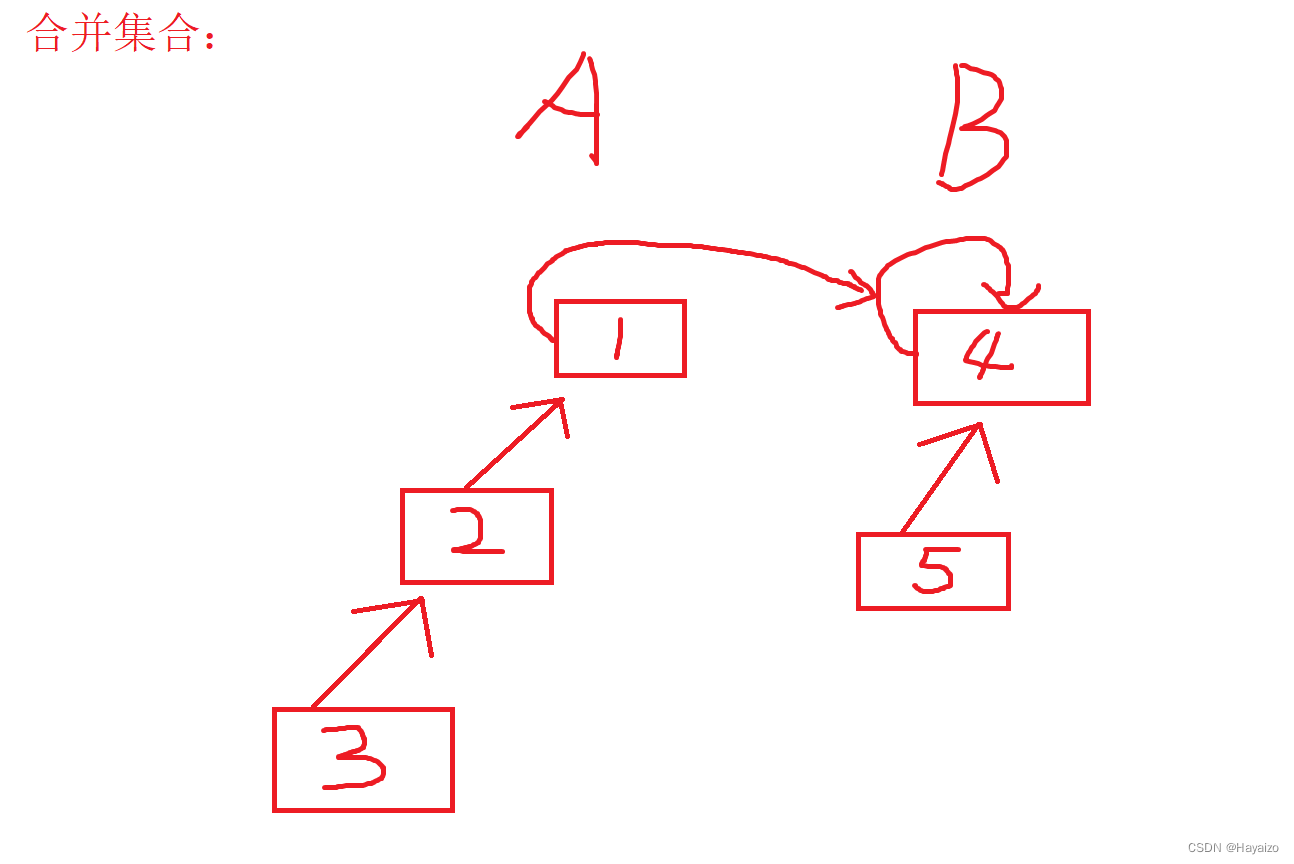
之前说到了，判断一个是不是属于同一个集合，就判断他们的祖宗节点是否一样，如果一样，这两个节点就是在同一个集合当中，那么合并A B两个节点，那么我们可以让A节点的祖宗节点设置为B的祖宗节点，那么A B这两个集合就合并了

合并集合

AC代码: 

#include<iostream>
using namespace std;
const int N=100010;
int p[N],n,m;int find(int x)
{if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int main(void)
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++) p[i]=i;while(m--){char op[5];int a,b;scanf("%s",op);if(op[0]=='M'){scanf("%d %d",&a,&b); p[find(a)]=p[find(b)];}else{scanf("%d %d",&a,&b);if(p[find(a)]==p[find(b)]) puts("Yes");else puts("No");}}return 0;
}

连通块中点的数量

 这题中的连通块我们可以看作集合中的元素，连接起来的连通块就是在一个集合当中，这题和上一题的区别就在于多了一个size大小，我们还需要维护一个size数组来记录当前集合中的元素个数，记录的方法就是当合并两个集合的时候，将A集合的size直接加到B集合中即可

AC代码

#include<iostream>
using namespace std;
const int N=100010;
int p[N],sz[N],n,m,a,b;int find(int x)
{if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int main(void)
{scanf("%d %d",&n,&m);for(int i=1;i<=n;i++) {p[i]=i;sz[i]=1;}while(m--){char op[5];scanf("%s",op);if(op[0]=='C'){scanf("%d %d",&a,&b);if(find(a)==find(b)) continue;sz[find(a)]+=sz[find(b)];p[find(b)]=p[find(a)];}else if(op[1]=='1'){scanf("%d %d",&a,&b);if(find(a)==find(b))puts("Yes");else puts("No");}else {scanf("%d",&a);printf("%d\n", sz[find(a)]);}}return 0;
}