目录
一、理想磁力计
二、硬铁效应
三、软铁效应
四、校正技术
五、使用函数magcal
5.1 仅偏移计算
编辑5.2 硬铁补偿和轴缩放计算
5.3 全硬铁和软铁补偿
5.4 自动拟合
六、 结论
七、程序
磁力计沿传感器的 X、Y 和 Z 轴检测磁场强度。精确的磁场测量对于传感器融合以及确定航向和方向至关重要。为了用于航向和方向计算,需要校准典型的低成本MEMS磁力计,以补偿环境噪声和制造缺陷。
一、理想磁力计
理想的三轴磁力计沿正交 X、Y 和 Z 轴测量磁场强度。在没有任何磁干扰的情况下,磁力计读数测量地球磁场。如果在传感器通过所有可能的方向旋转时进行磁力计测量,则测量值应位于球体上。球体的半径是磁场强度。 要生成磁场样本,请使用对象。出于这些目的,可以安全地假设每个方向的角速度和加速度为零。
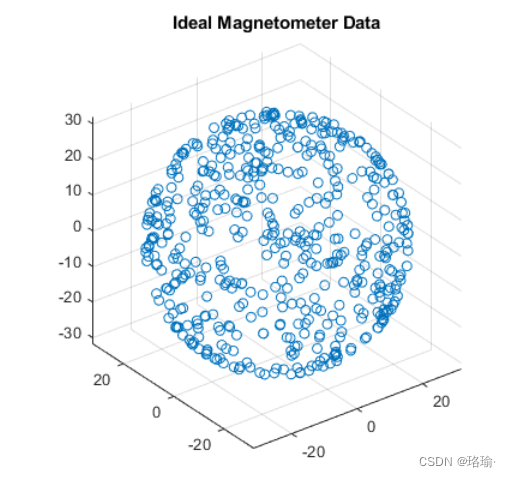
二、硬铁效应
噪声源和制造缺陷会降低磁力计的测量效果。其中最引人注目的是硬铁效应。硬铁效应是固定的干扰磁噪声源。通常, 这些来自带有磁力计的电路板上的其他金属物体.硬铁效应改变了理想球体的原点。

三、软铁效应
软铁效应更微妙。它们来自传感器附近的物体,这些物体会扭曲周围的磁场。这些具有拉伸和倾斜理想测量范围的效果。得到的测量值位于椭球体上。软铁磁场效应可以通过将IMU的地磁场矢量旋转到传感器帧,拉伸,然后将其旋转回全局帧来模拟。
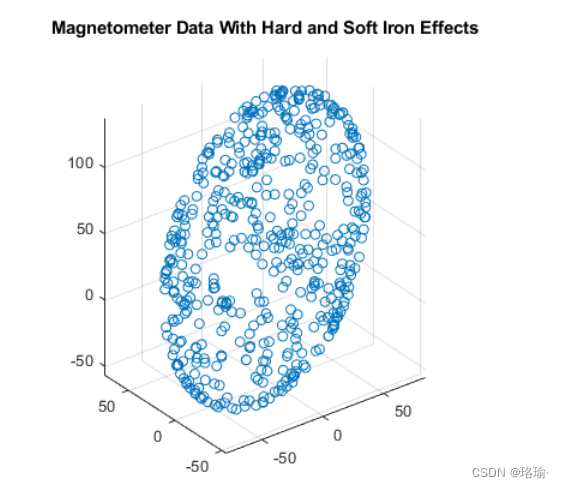
四、校正技术
该功能可用于确定考虑硬铁和软铁效应的磁力计校准参数。未经校准的磁力计数据可以建模为躺在椭圆体上,方程magcal
![]()
上面的方程是圆锥的一般形式。对于椭球体,R必须是正定的。该函数使用各种求解器,基于对R 的不同假设。在函数中,R可以假定为单位矩阵,对角矩阵或对称矩阵。
该函数产生校正系数,这些系数进行测量,这些测量位于偏移椭球体上,并将它们转换为位于以原点为中心的理想球体上。该函数返回一个 3×3 的实矩阵A和一个 1×3 的向量b。更正未校准的数据计算magcalmagcal
![]()
这里x是 1×3 的未校准磁力计测量数组,m是位于球体上的校正磁力计测量值的 1×3 阵列。矩阵A的行列式为 1,是R 的矩阵平方根。此外,A与R 具有相同的形式:单位、对角线或对称矩阵。由于这些类型的矩阵无法传递旋转,因此矩阵A在校正期间不会旋转磁力计数据。该函数还返回第三个输出,即磁场强度magcal.可以使用磁场强度来设定的属性。
五、使用函数magcal
使用该函数确定校正噪声磁力计数据的校准参数。通过设置属性来创建嘈杂的磁力计数据。使用变量中的旋转和拉伸磁场来模拟软铁效应。
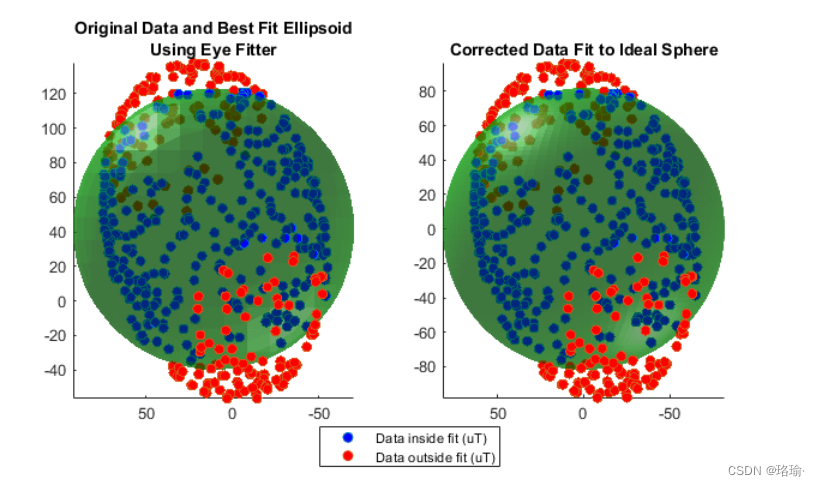
绘制原始数据和校正数据。显示最适合原始数据的椭球体。显示校正数据应位于的球体上。
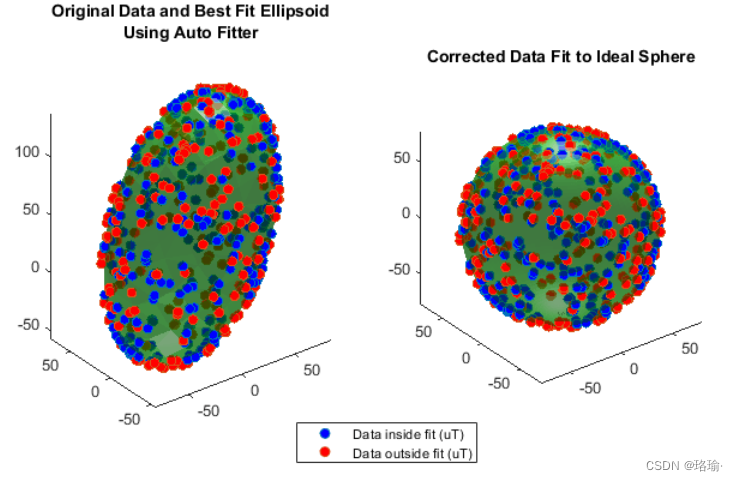
该函数使用各种求解器来最小化残余误差。残差是校准数据与半径球体之间距离的总和。
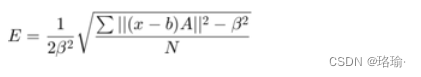
如果只需要校正某些缺陷或实现更简单的校正计算,则可以运行单个求解器。
5.1 仅偏移计算
许多MEMS磁力计在传感器内都有寄存器,可用于补偿硬铁偏移。实际上,上述等式的(x-b)部分发生在传感器上。当只需要硬铁偏移补偿时,矩阵实际上成为单位矩阵。要单独确定硬铁校正,可以这样调用该函数:Amagcal
 5.2 硬铁补偿和轴缩放计算
5.2 硬铁补偿和轴缩放计算
对于许多应用,将椭球矩阵视为对角矩阵就足够了。从几何上讲,这意味着未校准磁力计数据的椭球体近似为其半轴与坐标系轴对齐,并且与原点的中心偏移。虽然这不太可能是椭球体的实际特征,但它将校正方程简化为每个轴的单个乘法和单个减法。

5.3 全硬铁和软铁补偿
要强制函数求解任意椭球体并生成密集的对称矩阵,请按以下方式调用该函数:magcalA
5.4 自动拟合
应谨慎使用,和标志并检查输出值。在某些情况下,高阶(或)拟合的数据可能不足,可以使用更简单的矩阵找到一组更好的校正参数。没有足够的数据分布在椭球体的表面上,无法通过选件实现良好的拟合和适当的校准参数。使用 thefit 选项可以避免此问题,并找到一个更简单的矩阵,该矩阵是实数、对称和正定的。使用选项字符串调用与不使用任何选项字符串调用相同。比较使用 thefitter 和不正确的高阶拟合器的结果,可以显示在更正数据之前不检查返回的矩阵的危险。
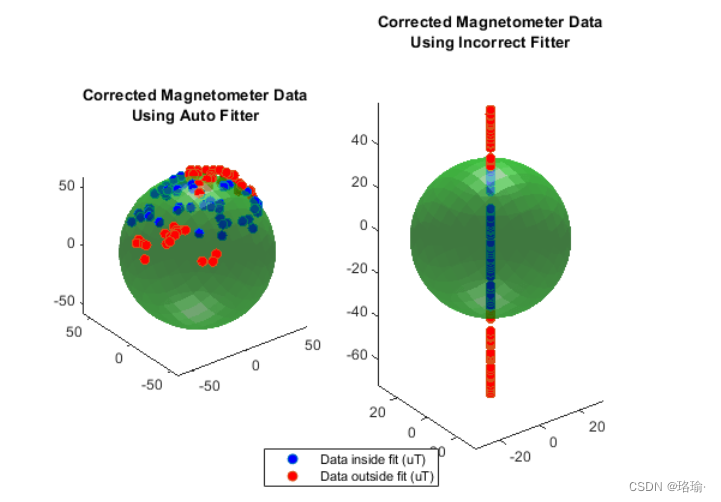
使用 theflag 调用函数(这是默认值)将尝试所有可能性,并搜索 theand,这将最小化残余误差,保持真实,并确保R是正定和对称的。
六、 结论
该功能可以提供校准参数,以校正磁力计中的硬铁和软铁偏移。在没有选项字符串或等效于选项字符串的情况下调用函数会产生最佳拟合并涵盖大多数情况。
七、程序
使用Matlab R2022b版本,点击打开。

打开下面的“MagnetometerCalibrationExample.m”文件,点击运行,就可以看到上述效果。
程序下载链接:https://download.csdn.net/download/weixin_45770896/87429222