科研中的部分依赖图（PDP）绘制

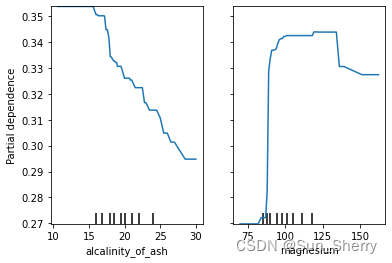
部分依赖图 Partial Dependence Plot

如今机器学习算法在各个领域被广泛应用，对于一些领域的科研来说，机器学习提供了更精确估计的可能，但是其弱解释性却成为了更深入研究的阻力。可解释机器学习就是在机器学习模型的基础上通过一系列方法使得模型结果具备可解释的特性，部分依赖图（Partial Dependence Plot）显示了一个或两个特征对机器学习模型的预测结果的边际效应，由于很多机器学习算法非参数的特性使得部份依赖图可以揭示线性以及非线性特征，容易理解并且有较高的解释力。

部分依赖图简易并且直观，在科学研究中被经常使用，但同时它也具有一些问题：

自变量间可能存在复杂的交互关系导致最终的结果，所以单看一个变量的pdp图可能是不全面的，然而由于人们对图形理解力的局限性，pdp图最多只支持双变量的交互而无法进行更高维的交互，当然这个缺陷的主要来源是人们的主观理解能力有限。
一些pdp图不显示特征分布，这可能会产生误导，因为可能会过度解释几乎没有数据的区域。
pdp假设其计算部分依赖的特征与其他特征不相关（在不进行交互的情况下），这可能会导致结果的误差，一个解决办法是使用条件而不是边际分布的累积局部效应图。（https://christophm.github.io/interpretable-ml-book/pdp.html）
由于pdp绘制的是平均响应，个体间的异质性可能无法被观察到，即有可能个体间的变化差异明显，这可以通过个体条件期望（Individual Conditional Expectation，ICE）曲线观察到。
取决于算法的精度以及难以避免的过拟合，pdp图可能存在许多较小的波动或变化趋势，而一般进行解释性研究时更加关注的是整体的变化趋势而不是局部变化。

sklearn的pdp方法

Python中重要的机器学习包sklearn在最近的更新中加入了pdp图的绘制方法，官方案例见：https://scikit-learn.org/stable/modules/partial_dependence.html?highlight=pdp

在这里插入图片描述

可以看到自带的绘图方法可以绘制单变量以及双变量交互的PDP图，并且还可以绘制ICE图，并且绘制的图形中包括了轴须图。不过根据上述的问题来看，sklearn提供的绘图方法轴须图太过稀疏，对样本分布的表征并不理想；其次缺少对曲线进行平滑拟合的表达。

pdp图绘制改进

基于以上的一些需求，我们可以自行绘制自己想要的pdp图，主要的思路就是使用sklearn的partial_dependence方法直接获取pd的值数组（https://scikit-learn.org/stable/modules/generated/sklearn.inspection.partial_dependence.html?highlight=partialdependence），然后使用其他的绘图包进行绘制。

下面是两种实践的代码，第一种包括了原曲线和拟合的样条曲线，并且使用了更密的轴须图，第二种在第一种的基础上增加了所有样本ICE的95%置信区间，这样可以看出样本间变化的异质性。不过需要注意的是这个置信区间是抽样估计的，与统计方法中参数估计的置信区间的意义是不同的。另外有一个小的细节是调用partial_dependence的时候如果不传入method参数则会自动使用‘recursion’方法，在一些模型中会导致pdp图的y轴是以0为基准值而不是以均值为基准值，而如果使用‘brute’方法则不会出现这种情况，但是会消耗更多的计算时间。

带拟合曲线与特征分布的pdp图

import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.inspection import partial_dependence # 直接获取pdp数组的方法
from scipy.interpolate import splev, splrep # 数据平滑插值features = list(importance.index)
for i in features:sns.set_theme(style="ticks", palette="deep", font_scale = 1.3)fig = plt.figure(figsize=(6, 5), dpi=100)ax  = plt.subplot(111)pdp = partial_dependence(model, X, [i], kind="average", method = 'brute', grid_resolution=50) # 获取pdp的数组plot_x = pdp['values'][0] # 提取值作为x轴plot_y = pdp['average'][0] # 提取平均pdp作为y轴数据tck = splrep(plot_x, plot_y, s=30) # 进行数据平滑，参考：https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html?highlight=interpolatexnew = np.linspace(plot_x.min(),plot_x.max(),300)ynew = splev(xnew, tck, der=0)plt.plot(plot_x, plot_y, color='k', alpha=0.4) # 绘制原曲线plt.plot(xnew, ynew, linewidth=2) # 绘制平滑曲线sns.rugplot(data = dummy_df.sample(100), x = i, height=.06, color='k', alpha = 0.3) # 使用sns绘制轴须图x_min = plot_x.min()-(plot_x.max()-plot_x.min())*0.1 # 定义x轴的下限x_max = plot_x.max()+(plot_x.max()-plot_x.min())*0.1 # 定义X轴的上限plt.title('Partial Dependence Plot of '+i , fontsize=18)plt.ylabel('Partial Dependence')plt.xlim(x_min,x_max) # 定义X轴的上下限，为了防止轴须图中的离散值改变了坐标轴定位plt.savefig('./pdpplot_'+i+'.jpg')plt.show()

绘制结果如下：
在这里插入图片描述

带ICE置信区间的pdp图

import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.inspection import partial_dependence # 直接获取pdp数组的方法
from scipy.interpolate import splev, splrep # 数据平滑插值features = list(importance.index)
for i in features:pdp = partial_dependence(model, X, [i], kind="both", grid_resolution=50) # 这里采用了both方法，除了pdp均值外会计算出每个样本的icesns.set_theme(style="ticks", palette="deep", font_scale = 1.1)fig = plt.figure(figsize=(6, 5), dpi=100)ax  = plt.subplot(111)plot_x = pd.Series(pdp['values'][0]).rename('x')plot_i = pdp['individual'] #获取每个样本的ice数组plot_y = pdp['average'][0]tck = splrep(plot_x, plot_y, s=30)xnew = np.linspace(plot_x.min(),plot_x.max(),300)ynew = splev(xnew, tck, der=0)plot_df = pd.DataFrame(columns=['x','y']) # 定义一个新df，包括x y两列for a in plot_i[0]: # 遍历每个样本的icea2 = pd.Series(a)df_i = pd.concat([plot_x, a2.rename('y')], axis=1) # 将ice与x横向拼接plot_df = plot_df.append(df_i) # 加入到总表中sns.lineplot(data=plot_df, x="x", y="y", color='k', linewidth = 1.5, linestyle='--', alpha=0.6) # 使用sns绘制线图，如果同一个x上有多个y的话将会自动生成95%置信区间plt.plot(xnew, ynew, linewidth=2)  sns.rugplot(data = dummy_df.sample(100), x = i, height=.05, color='k', alpha = 0.3)x_min = plot_x.min()-(plot_x.max()-plot_x.min())*0.1x_max = plot_x.max()+(plot_x.max()-plot_x.min())*0.1plt.title('Partial Dependence Plot of '+i , fontsize=18)plt.ylabel('Partial Dependence')plt.xlabel(i)plt.xlim(x_min,x_max)plt.savefig('./pdpplot_'+i+'.jpg')plt.show()