关于对贝叶斯与认知问题的相关思考
- 一、贝叶斯定理
- 二、贝叶斯与认知的本质
- 三、经验的偏见
- 四、总结

自古以来,人们就在思考知识来自何处,“冯翼惟象,何以识之?”,对此的思考逐渐发展成哲学的认识论分支。德国哲学家康德指出,“所有人类知识从直觉开始,然后转变为观念,最后化为思想”。法国数学家拉普拉斯进一步阐释到,“概率论本质不过是化为计算的常识,它以准确的方式评价那些政策的头脑通过某种直觉领会到的东西,而这种直接领会经常不被察觉”。
人类认识研究自然、开展社会实践,包括现在的人工智能都遵循着,做出假设、收集数据、判断决策、观察结果、修正假设的周而复始的类似过程。
贝叶斯公式通过简洁的数学形式,将人类的基本感知与高级推理相结合,定义了人类对世界的认知过程。根据贝叶斯公式,我们不断获取有效的知识,英国靠它破译二战德军密码,医疗业靠它辅助诊断,银行业靠它发放贷款,互联网靠它推荐商品,而人工智能更是靠它实现了飞跃。
一、贝叶斯定理
1763年12月23日,托马斯·贝叶斯的遗产受赠者R. Price牧师在英国皇家学会宣读了贝叶斯的遗作《An essay towards solving a problem in the doctrine of chances》(《论机会学说中一个问题的求解》),其中给出了贝叶斯定理。贝叶斯定理是一种统计学方法,其基本工具就是贝叶斯公式: P ( A ∣ B ) = P ( A ) P ( B ∣ A ) / P ( B ) P(A|B)=P(A)P(B|A)/P(B) P(A∣B)=P(A)P(B∣A)/P(B)其中, P ( A ) P(A) P(A)为事件 A A A的先验概率, P ( A ∣ B ) P(A|B) P(A∣B)为事件 B B B条件下,事件A的后验概率; P ( B ) P(B) P(B)为事件 B B B的先验概率, P ( B ∣ A ) P(B|A) P(B∣A) 为事件 A A A条件下,事件 B B B的后验概率。

贝叶斯定理广泛应用于各个领域的推断、决策中。以医疗诊断为例,假设肺癌发病率 P ( A ) = 0.001 P(A)=0.001 P(A)=0.001,吸烟人群占比 P ( B ) = 0.4 P(B)=0.4 P(B)=0.4,而肺癌病人中有 80 % 80\% 80%吸烟 ,即 P ( B ∣ A ) = 0.8 P(B|A)= 0.8 P(B∣A)=0.8,则若某患者吸烟,则该患者肺癌的概率: P ( A ∣ B ) = P ( A ) P ( B ∣ A ) / P ( B ) = 0.001 ∗ 0.8 / 0.4 = 0.002 P(A|B)=P(A) P(B|A)/P(B)=0.001*0.8/0.4 =0.002 P(A∣B)=P(A)P(B∣A)/P(B)=0.001∗0.8/0.4=0.002该例中,贝叶斯公式将先验概率 P ( A ) P(A) P(A)转化为了后验概率 P ( A ∣ B ) P(A|B) P(A∣B),这个过程中主要利用了观察数据 P ( B ∣ A ) P(B|A) P(B∣A) 。肺癌发病率只有 P ( A ) = 0.001 P(A)=0.001 P(A)=0.001,但是根据观察数据发现,肺癌病人的吸烟者比率 P ( B ∣ A ) = 0.8 P(B|A)= 0.8 P(B∣A)=0.8高于整体人群的吸烟者占比 P ( B ) = 0.4 P(B)=0.4 P(B)=0.4,因此增强了吸烟者中肺癌发病率的信念。
二、贝叶斯与认知的本质
贝叶斯定理之所以得到广泛应用,核心在于其本质符合人类认识的普遍规律与日常解决问题的通用方式,即“我”对客观世界总有一个主观的先验判断,但这个判断会随着“我”对真实世界的观察而修正,从而对世界永远保持开放的态度。其中,贝叶斯公式中的先验概率代表初始的主观判断,实质上也是经验统计的结果(先验信息一般来自历史经验与资料、甚至直觉),而后验概率代表对当前真实世界的观测(一般来自于当前的实践过程、观测数据)。
贝叶斯定理从“观察者”角度(即“人”的角度)出发,认为概率是主观对某个事物发生的相信程度,由于“观察者”知识的不完备,需要不断从对客观世界的观察中得到规律更新对事件的假设。
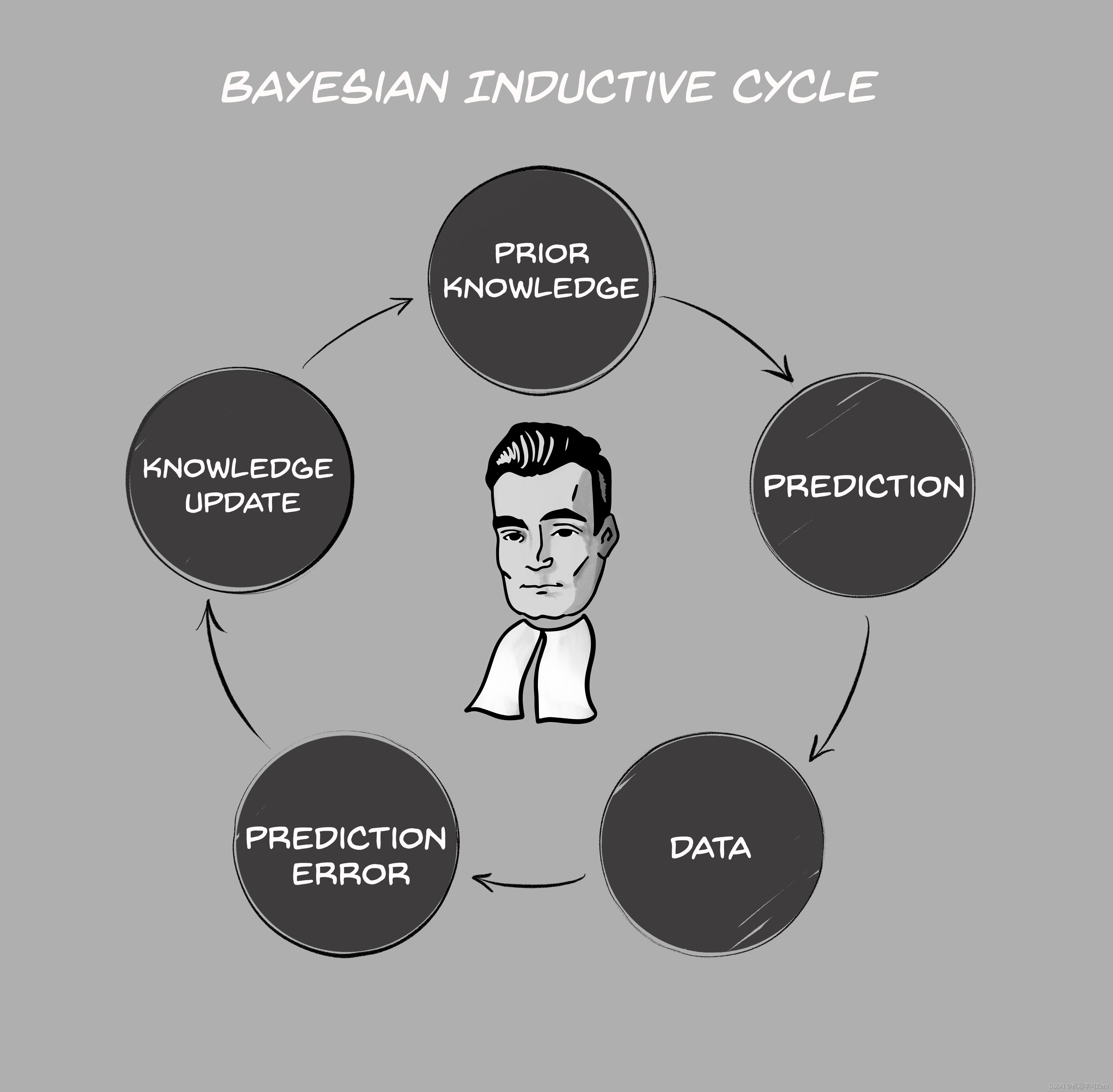
从这点来说,贝叶斯定理与马克思主义哲学的基本观点也是一致的。马克思主义哲学认为,人的认识都是一步步由低级向高级发展,即由浅入深,由片面到更多的方面。认识的过程分为感性阶段与理性阶段,感性阶段是开始接触外界事情,属于感觉的阶段;理性阶段是综合感觉的材料加以整理和改造,属于概念、判断和推理的阶段。理性认识依赖于感性认识,感性认识有待于发展到理性认识,这是辩证唯物论的认识论。

同时马克思主义深刻指出,只有人的社会实践,才是人们对于外界认识的真理性的标准。实践就是不断的观察世界,获取新的数据的过程,而发展真理则是不断对主观判断的修正。在实践过程中,人们达到预期结果时,认识才被证实。要想得到预期结果,一定要使自己的认知符合客观规律,否则就会在实践中失败。而经过失败后,从失败取得教训,改正自己的认识使之符合客观规,就能变失败为胜利,所谓“失败者成功之母”,“吃一堑长一智”。
三、经验的偏见
贝叶斯定理中“观察者”基于经验会对事件有个初始判断,而基于经验的判断往往存在不同程度的偏差。

《贝叶斯的博弈》一书中引用了阿莫斯·特沃斯基和丹尼尔·卡内曼两位心理学研究者提出的“琳达问题”:琳达31岁,独身,为人诚恳且充满智慧。她学习过哲学。她在还是大学生的时候就很关心歧视与社会正义的问题,也曾参加反核游行。下面哪个陈述更有可能正确:A.琳达是银行办事员。B.琳达是银行办事员,并且活跃在女权运动中。在该问题的多次实验中,85%以上的测试者选择了错误答案B。实际上,B是A的特殊情况,即B是A的子集,从概率上来说 P ( B ) ≤ ( A ) P(B)≤(A) P(B)≤(A),因此A是正确答案。特沃斯基和卡内曼认为,针对此类问题,人们更多是进行关联性的推理,而非数学推理,对于31岁、独身、接受过高等教育、参加过反歧视运动的女性的此类特征,选项B更令人信服。
尼曼和特沃斯基还发现,在回答“A物体是否属于S类”这种问题时,由于经验的偏见,人们容易出现代表性偏差。比如A是个害羞的人,他更可能是围棋选手还是销售员?大多数人会感觉A肯定更应该是围棋选手,因为害羞像围棋选手的代表性特征,而对销售员来说,这个特点太过异常。
然而,属于某一类的可能性还要受其他许多重要因素的影响。该例子中,A是围棋选手还是销售员还的可能性大,主要是受这两种职业在总人口中所占相对比例的影响。假设总人口中销售员所占比是20%,围棋选手则是0.1%,而10%的销售员害羞,而围棋选手害羞的有90%。则每1000人,害羞的销售员是20人,而害羞的围棋选手只有0.9人,因此此类情况下,一个害羞的人更可能是一个围棋选手。
通过上述例子,可以看出仅靠经验或理论做出的判断往往会造成偏见。《贝叶斯的博弈》中写到,“我们都是本能上不能理性的笨蛋,无法正确修订我们的信念,而理解贝叶斯的这个法则真的可以帮助改善我们自身”。

因此,要解决问题就不能仅靠理论或经验,要充分调查研究,结合客观实际具体问题具体分析。“没有调查,就没有发言权”,调查研究的过程就是对当前情况充分观测、获取数据的过程,从而将理论与客观实际相结合,看它是否在实践中能够达到预期。

许多科学理论之所以被称为真理,不在于科学家们创立这些学说的时候,而且在于为尔后的科学实践所证实的时候。人类认识的历史告诉我们,许多理论的真理性是不完全的,经过实践的检验而纠正了它们的不完全性。许多理论是错误的,经过实践的检验而纠正其错误。实践是检验真理的唯一标准,所谓“生活、实践底观点,应该是认识论底首先的和基本的观点”。
四、总结
“根据贝叶斯定理,任何理论都不完美。取而代之的是一项未尽的工作,它永远处于推敲与测试之中。”贝叶斯状态就是一种平衡于确信与怀疑之间的状态,在这种状态下,人们不会轻易相信谣言,也可以勇敢挑战权威。

正像毛泽东同志《实践论》指出的那样,“通过实践而发现真理,又通过实践而证实真理和发展真理。从感性认识而能动地发展到理性认识,又从理性认识而能动地指导革命实践,改造主观世界和客观世界”。实践、认识、再实践、再认识,这种形式,循环往复以至无穷,而实践和认识之每一循环的内容,都比较地进到了高一级的程度,这就是辩证唯物论的全部认识论,也就是所谓“知行合一”。



