很多博客都在讲倒角距离变换（chamfer distance transform），看完之后，我对倒角距离仍然是一片雾水。因此，在这篇文章论述一下我对倒角距离的理解。

前言：距离变换

距离变换的主要目的是通过识别目标点与背景点，将二值化图像转化为灰度图。
距离变换主要分为欧式距离变换和非欧式距离变换，非欧式距离变换包括棋盘距离变换、城市街区距离变换、倒角距离变换。
城市街区距离：$|x_1-x_2|+|y_1-y_2|$
棋盘距离：$max(|x_1-x_2|,|y_1-y_2|)$

2D图像中的倒角距离

倒角距离的定义，倒角距离是两条曲线或两个二进制图像之间的距离。
The Chamfer distance is a sum of positive distances and is defined for unsigned distance functions. In the case of two-dimensional template matching using Chamfer distance, the reference image and the template are both binary edge images which can be obtained using an edge filter on the original images.
倒角距离是一些距离之和，为了无符号的距离函数所定义。

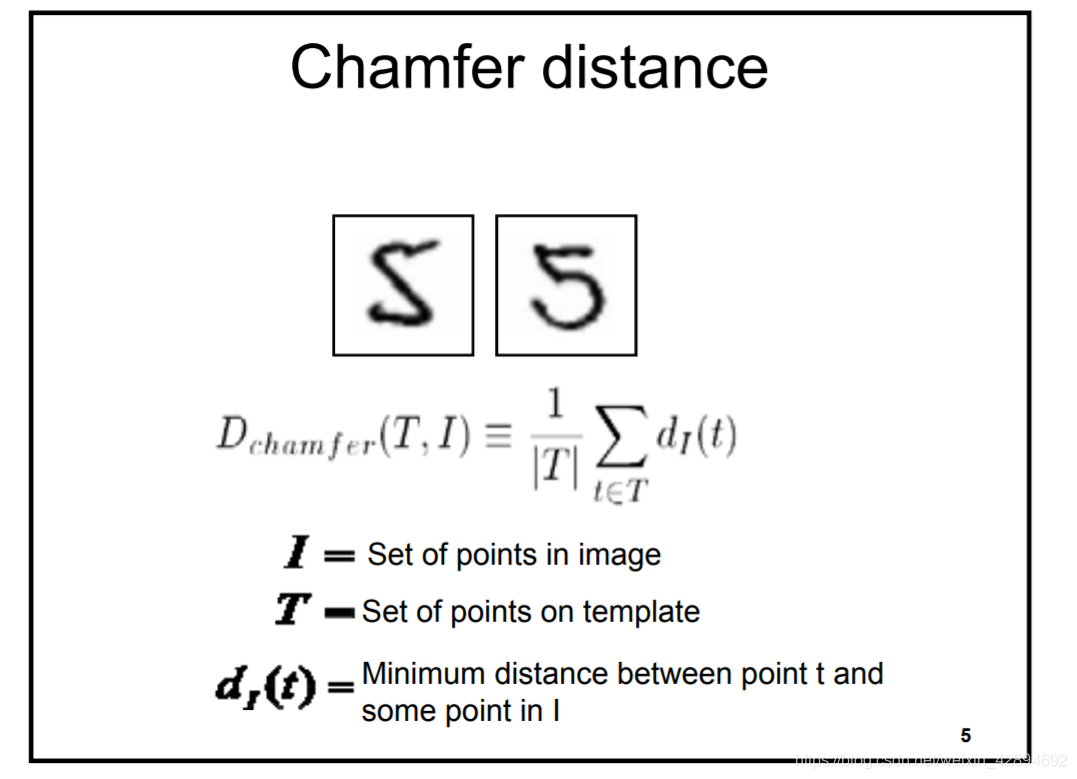
例如，我们要对齐上图中两个数字5，此时倒角距离的定义为模板 $T$ 中一点 $t$ 和图像 $I$ 中某点最小距离的平均值。

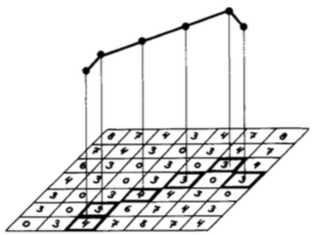
2D图像的距离变换

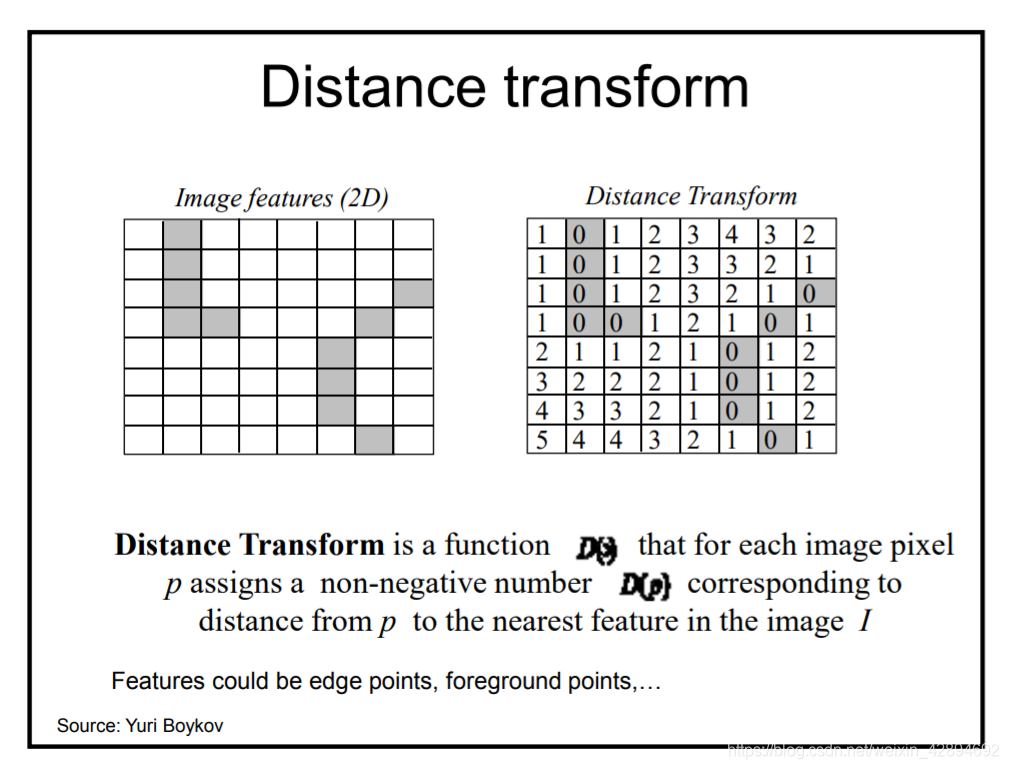
距离变换是一个距离函数$D(p)$，数值对应像素$p$距离图像$I$中最近特征的距离。上图中，灰色为特征，右侧为距离变换之后得到的图像。

3D点云中的倒角距离

3D空间的倒角距离主要用于点云重建或者3D重建工作。定义如下：

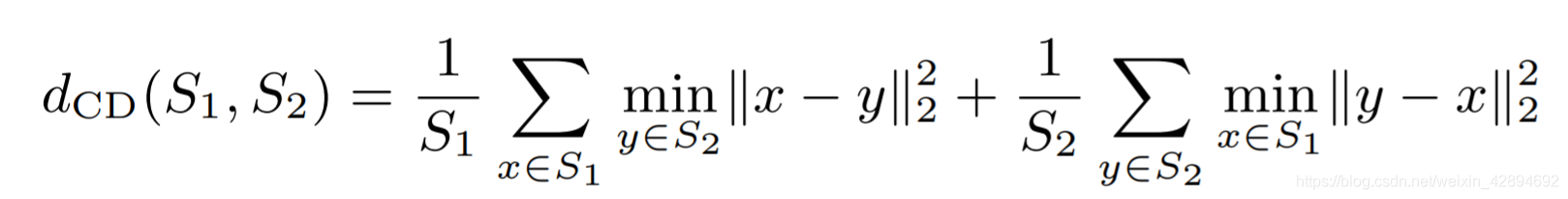
以上公式的$S_1,S_2$分别表示两组3D点云，第一项代表$S_1$中任意一点$x$到$S_2$的最小距离之和，第二项则表示$S_2$中任意一点$y$到$S_1$的最小距离之和。
如果该距离较大，则说明两组点云区别较大；如果距离较小，则说明重建效果较好。
一般来说，该距离用作3D重建网络的损失函数。