排序算法性能分析

news/2025/2/18 23:09:53/

目录

实现插入排序、冒泡排序、选择排序、合并排序、快速排序算法（从小到大）

①插入排序

②冒泡排序

③选择排序

⑥快速排序

五种排序

现在有10亿的数据（每个数据四个字节），请快速挑选出最大的十个数，并在小规模数据上验证算法的正确性。

方法一：规模为10的插入排序

方法二：规模为10的堆排序

实现插入排序、冒泡排序、选择排序、合并排序、快速排序算法（从小到大）

首先介绍各个排序算法的设计思路以及给出各个算法的伪代码，再通过伪代码具体实现每个排序算法。

①插入排序

设计思路：

假设前N-1个数已经是有序序列了，那么将第N个数插入其中仍使其有序的方法是依次和前N-1个数进行比较，找到合适的位置安放即可。

开始时，将第一个数作为有序序列，先从第2个数开始插入，重复操作，直到排序完成。

将1，2，3，4，4，9作为插入排序的例子，如图1所示。

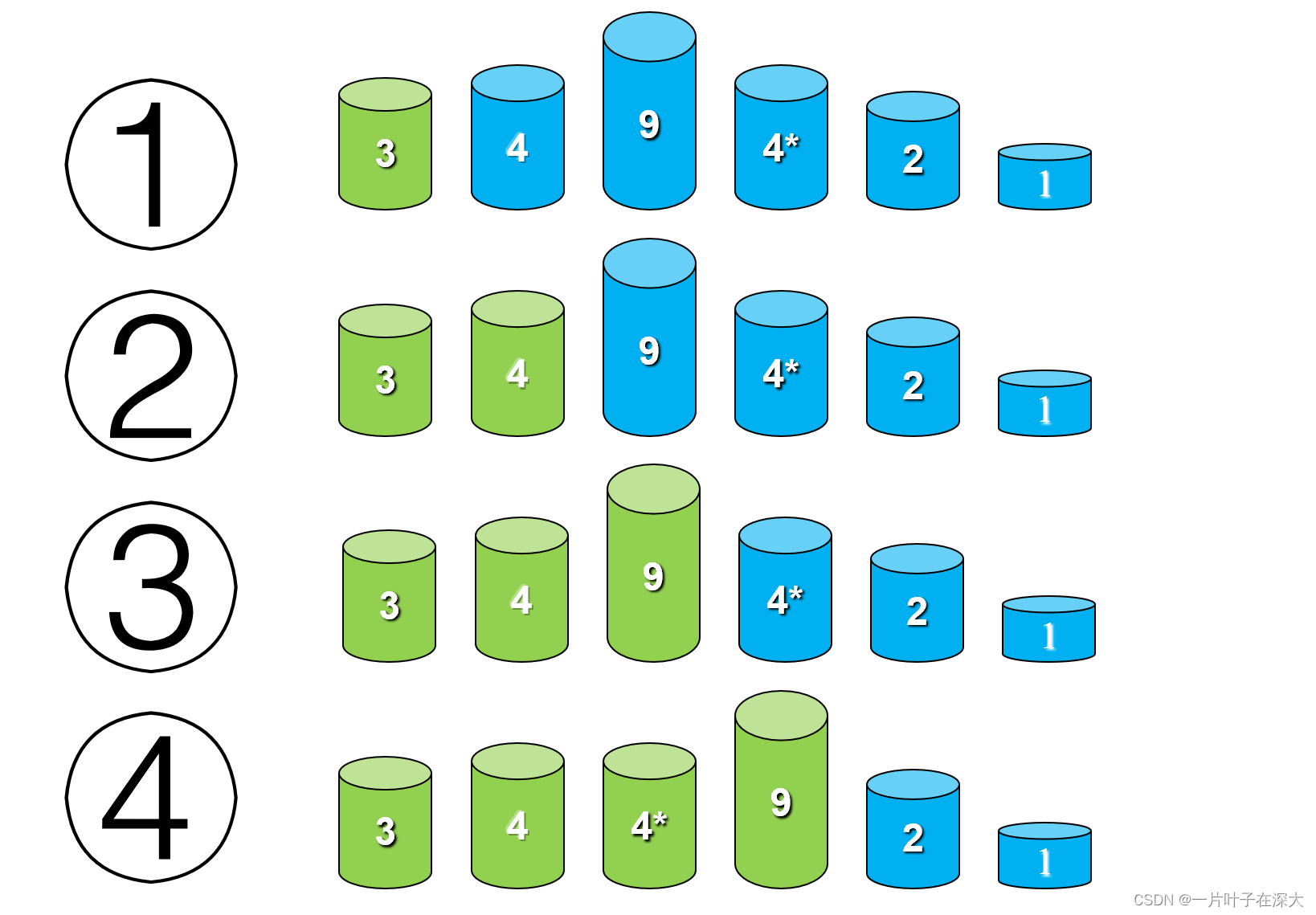
图1 插入排序图示

伪代码：

matlab代码

result=[];
for power=1:5scale=power*10000;count=0;for times=1:20number=randi(scale,1,scale);tic;for i=1:scale-1for j=i+1:-1:2if number(j)>number(j-1)breakelsetemp=number(j);number(j)=number(j-1);number(j-1)=temp;endendendcount=count+toc;           endcount=count/20;result=[result,count];
end

算法复杂度分析：

最坏时间复杂度：O(n^2）

最好时间复杂度：O(n)

平均时间复杂度：O(n^2)

实际效率：

随机生成数据规模分别为10000，20000，30000，40000，50000的测试数据，每个数据规模记录20组的平均排序时间，数据记录如表1所示。

表1 插入排序

其中取第一个实验值作为理论值基准计算出理论值，如图2所示。

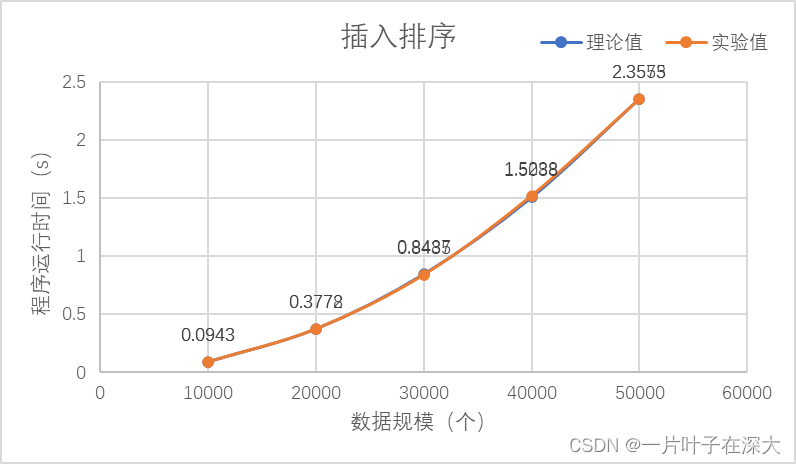
图2 插入排序

解释与分析：

由图2可知，在不同的数据规模下，插入排序的实验数据和理论计算基本一致。

②冒泡排序

设计思路：

比较相邻两个元素的大小，如果大小顺序不对则交换位置，这样一趟下来，最大的或者最小的就可以被分离出来，如此重复下去，直到排序完成。

将8，16，21，25，27，49作为冒泡排序的例子，如图3所示。

图3 冒泡排序图示

伪代码：

matlab代码

result=[];
for power=1:5scale=power*100;count=0;for times=1:20number=randi(scale,1,scale);tic;for i=scale:-1:1for j=1:i-1if number(j)>number(j+1)temp=number(j);number(j)=number(j+1);number(j+1)=temp;endendendcount=count+toc;           endcount=count/20;result=[result,count];
end

算法复杂度分析：

最坏时间复杂度：O(n^2）

最好时间复杂度：O(n^2)

平均时间复杂度：O(n^2)

实际效率：

随机生成数据规模分别为10000，20000，30000，40000，50000的测试数据，每个数据规模记录20组的平均排序时间，数据记录如表2所示。

表2 冒泡排序

其中取第一个实验值作为理论值基准计算出理论值，如图4所示。

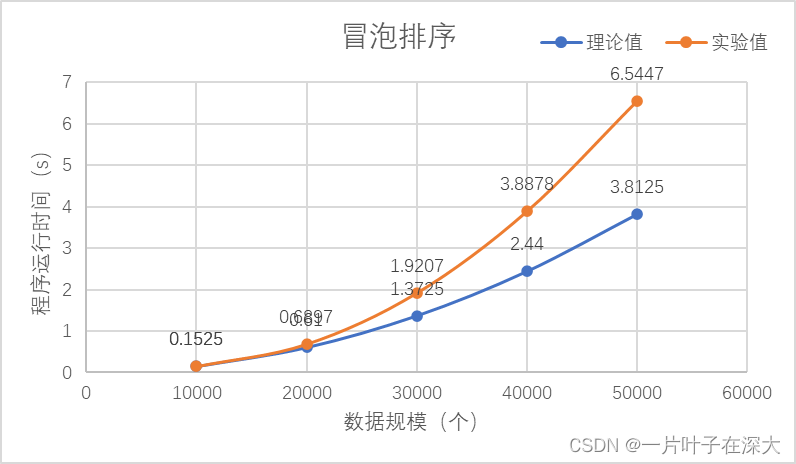
图4 冒泡排序

解释与分析：

由图4可知，冒泡排序的实验数据比理论计算要大，并且随着数据规模的增大，这个差距也在增大，初步分析是数据规模小，所取的理论值基准较小，加上运行环境影响所致。

③选择排序

设计思路：

每次在序列中找出最小的元素，将它与第一个元素交换位置，接着找剩下序列中最小的元素，将它与第二个元素交换位置，如此重复，直到排序完成。

将8，16，21，25，27，49作为选择排序的例子，如图5所示。

图5 选择排序图示

伪代码：

matlab代码

result=[];
for power=1:5scale=power*10000;count=0;for times=1:20number=randi(scale,1,scale);tic;for i=1:scale-1for j=i+1:scaleif number(i)>number(j)temp=number(j);number(j)=number(i);number(i)=temp;endendendcount=count+toc;           endcount=count/20;result=[result,count];
end

算法复杂度分析：

最坏时间复杂度：O(n^2）

最好时间复杂度：O(n^2)

平均时间复杂度：O(n^2)

实际效率：

随机生成数据规模分别为10000，20000，30000，40000，50000的测试数据，每个数据规模记录20组的平均排序时间，数据记录如表3所示。

表3 选择排序

其中取第一个实验值作为理论值基准计算出理论值，如图6所示。

图6 选择排序

解释与分析：

由图6可知，在不同的数据规模下，选择排序的实验数据和理论计算基本一致。

（4）归并排序

设计思路：

把序列分成很多的子序列，先每两个元素合并成一个有序序列，再每四个元素合并成一个有序序列，如此下去，直到整个序列有序。

将8，16，21，25，25*，49作为归并排序的例子，如图7所示。

图7 归并排序图示

伪代码：

matlab代码

result=[];
for power=1:5scale=power*100000;count=0;for times=1:20number=randi(scale,1,scale);done=zeros(1,scale);tic;step=1;
%         number=MergeSort(1,scale,number,done);while step<scalefor low=1:2*step:scalemid=low+step-1;if mid>scalebreakendhigh=low+2*step-1;if high>scalehigh=scale;enddone=Merge(low,mid,high,number,done);endstep=step*2;number=done;endcount=count+toc;           endcount=count/20;result=[result,count];
end
% function[number]=MergeSort(low,high,number,done)
%     if low<high
%         mid=floor((low+high)/2);
%         number=MergeSort(low,mid,number,done);
%         number=MergeSort(mid+1,high,number,done);
%         number=Merge(low,mid,high,number,number);
%     end
% end
function[done]=Merge(low,mid,high,number,done)i=low;j=mid+1;k=low;while i<=mid&&j<=highif number(i)<=number(j)done(k)=number(i);i=i+1;elsedone(k)=number(j);j=j+1;endk=k+1;endwhile i<=middone(k)=number(i);k=k+1;i=i+1;endwhile j<=highdone(k)=number(j);k=k+1;j=j+1;end
end

算法复杂度分析：

最坏时间复杂度：O(nlogn）

最好时间复杂度：O(nlogn)

平均时间复杂度：O(nlogn)

实际效率：

随机生成数据规模分别为10000，20000，30000，40000，50000的测试数据，每个数据规模记录20组的平均排序时间，数据记录如表4所示。

表4 归并排序

其中取第一个实验值作为理论值基准计算出理论值，如图8所示。

图8 归并排序

解释与分析：

由图8可知，归并排序的实验数据比理论计算要大，并且随着数据规模的增大，这个差距也在增大，初步分析是数据规模较小，所取的理论值基准较小，加上运行环境影响所致。

⑥快速排序

设计思路：

先取一个中轴元素，比如第一个元素，然后根据这个中轴元素将序列分成两个子序列，一个子序列里面的元素都比中轴元素小，另一个子序列里面的元素都比中轴元素大，然后再对子序列进行这样的操作，如此重复，直到排序完成。

将8，16，21，25，25*，49作为快速排序的例子，如图9所示。

图9

伪代码：

matlab代码

result=[];
for power=1:5scale=power*10000;count=0;for times=1:20number=randi(scale,1,scale);tic;number=Quick(1,scale,number);count=count+toc;           endcount=count/20;result=[result,count];
end
function[number]=Quick(low,high,number)i=low;j=high;pivot=number(low);while low<highwhile low<high&&pivot<=number(high)high=high-1;endif low<highnumber(low)=number(high);low=low+1;endwhile low<high&&pivot>number(low)low=low+1;endif low<highnumber(high)=number(low);high=high-1;endendnumber(low)=pivot;if i<low-1number=Quick(i,low-1,number);endif high+1<jnumber=Quick(high+1,j,number);end
end

算法复杂度分析：

最坏时间复杂度：O(n^2）

最好时间复杂度：O(nlogn)

平均时间复杂度：O(nlogn)

实际效率：

随机生成数据规模分别为10000，20000，30000，40000，50000的测试数据，每个数据规模记录20组的平均排序时间，数据记录如表5所示。

表5 快速排序

其中取第一个实验值作为理论值基准计算出理论值，如图10所示。

图10 快速排序

解释与分析：

由图10可知，快速排序的实验数据比理论计算要小，初步分析是数据规模小，所取的理论值基准较小，加上运行环境影响所致。

五种排序

以上五种排序实际运行效率如图11所示。

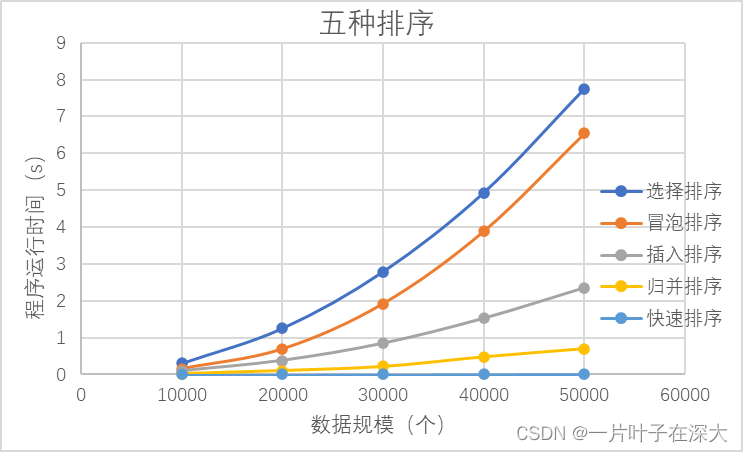
图11 五种排序比较

由图可以看出五种排序实际效率最快的是平均时间复杂度为O(nlogn)的快速排序和归并排序，然后是最优时间复杂度为O(n)的插入排序，最后是时间复杂度均为O(n^2)的冒泡排序和选择排序。

现在有10亿的数据（每个数据四个字节），请快速挑选出最大的十个数，并在小规模数据上验证算法的正确性。

算法设计思路：

对于10亿个数据从中挑选出最大的十个数，对10亿个数全部进行排序的方法显然不可取，可以通过选择排序或者冒泡排序进行10趟排序，但是这样需要进行的操作次数大概是100亿次，这里我们采取别的方法。

方法一：规模为10的插入排序

我们首先对前10个数进行降序排序，这样末尾的数是前10个数中最小的数，此后遍历剩下的10亿-10个数，对每一个数都和前10个数进行一趟插入排序，最少比较次数为1次，最多比较次数为10次，这样需要进行的操作次数大概是55亿次，比冒泡排序和选择排序减少了近一半的操作次数。

matlab代码

result=[];
for power=1:1scale=power*1000000000;count=0;for times=1:20numbers=randi(scale,1,scale);number=numbers(1,1:10);tic;for i=1:9for j=i+1:-1:2if number(j)<number(j-1)breakelsetemp=number(j);number(j)=number(j-1);number(j-1)=temp;endendendfor i=11:scalefor j=10:-1:1if number(j)>=numbers(i)breakelseif j<10number(j+1)=number(j);endnumber(j)=numbers(i);endendend      count=count+toc;           endcount=count/20;result=[result,count];
end

实际表现：

取数据规模为100W，200W，300W，400W，500W作为测试数据，每个数据规模测试20组，记录平均运行时间，如图12所示。

图12 规模为10的插入排序

测试一些大数据的运行时间（20组平均时间）如下：

一千万：0.0390s

五千万：0.1832s

一亿：0.3727s

五亿：1.8612s

十亿：5.6923s

方法二：规模为10的堆排序

方法一的规模为10的插入排序效率已经比较高了，但是仍有不足，即将10个最大的数也进行了排序，而实际上只需要将它们挑选出来即可，考虑建立规模为10的堆排序，这样最小比较次数为1次，但最大比较次数降到了3次，挑出10个最大的数理论上大概需要进行20亿次的操作即可。

matlab代码 

result=[];
for power=1:1scale=power*1000000000;count=0;for times=1:20numbers=randi(scale,1,scale);number=numbers(1,1:10);tic;for i=5:-1:1number=Adjust(i,10,number);endfor i=11:scaleif numbers(i)>number(1)number(1)=numbers(i);number=Adjust(1,10,number);endend      count=count+toc;           endcount=count/20;result=[result,count];
end
function[number]=Adjust(i,m,number)temp=number(i);j=2*i;while j<=mif j<m&&number(j)>number(j+1)j=j+1;endif number(j)>=tempbreakendnumber(i)=number(j);i=j;j=j*2;endnumber(i)=temp;
end
% function[number]=HeapSort(number,scale)
%     for i=scale:-1:2
%         temp=number(1);
%         number(1)=number(i);
%         number(i)=temp;
%         number=Adjust(1,i-1,number);
%     end
% end

实际表现：

取数据规模为100W，200W，300W，400W，500W作为测试数据，每个数据规模测试20组，记录平均运行时间，与插入排序相比，效率明显提升，如图13所示。

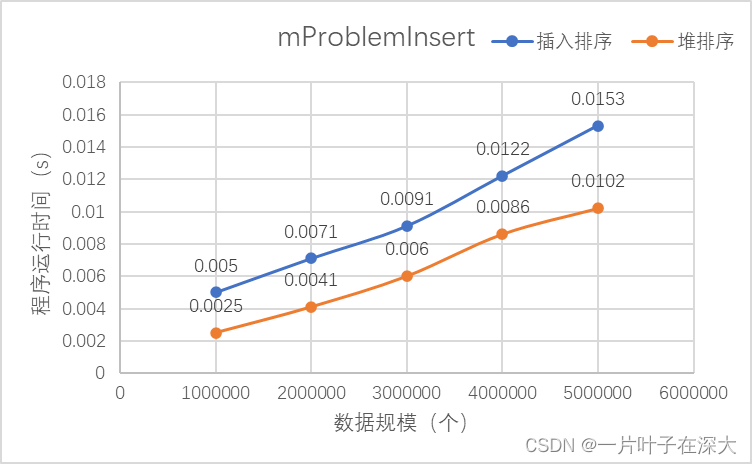
图13 规模为10的堆排序

测试一些大数据的运行时间（20组平均时间）如下：

一千万：0.0201s

五千万：0.1059s

一亿：0.2001s

五亿：1.0711s

十亿：4.6140s


http://www.ppmy.cn/news/788852.html

相关文章

Vue3+Vite+Pinia+Naive项目搭建之二：scss 的安装和使用

Vue3+Vite+Pinia+Naive项目搭建之二：scss 的安装和使用

前言 如果对 vue3 的语法不熟悉的&#xff0c;可以移步 Vue3.0 基础入门&#xff0c;快速入门。 1. 安装依赖 yarn add sass -D // or npm install sass -D 2. 页面样式初始化 reset.scss /* 新建 src/assets/style/reset.scss */ /* 页面样式初始化 */ html, body, div, s…
阅读更多...
Homekit智能球泡灯

Homekit智能球泡灯

五路Homekit智能球泡灯&#xff0c;实际瓦数&#xff1a;9W&#xff0c;E27接口&#xff0c;支持苹果Homekit扫码直连Siri控制&#xff0c;也可在Cozylife app内绑定智能音箱搭配使用&#xff0c;支持包括&#xff08;Alexa、Google Home、小爱音箱、天猫精灵、小度音箱等&…
阅读更多...
Zigbee实现呼吸灯效果

Zigbee实现呼吸灯效果

** CC2530实现呼吸灯效果 ** 编程实现 PWM 输出驱动 LED , 控制 PWM 电平的宽度,逐渐改变 PWM 的占空比来使得 LED 能够模拟呼吸过程长 —— 由渐暗到渐亮,渐亮到渐暗, 如此反复,利用 LED 余辉和人眼的暂留效应,实现模拟呼吸过程。 我们利用CC2530的定时器1的自由运行模式输…
阅读更多...
智能家居DIY的又一神器ESPEasy For ioBroker

智能家居DIY的又一神器ESPEasy For ioBroker

上一期我们讲了ESPHome&#xff0c;大家觉得简单吗&#xff1f;今天我给大家带来的是另外一个完全不用代码的ESPEasy&#xff01; 首先我们在官网下载最新版本的ESPEasy&#xff0c;如果大家因为墙的原因无法下载&#xff0c;我在这里提供百度网盘下载&#xff0c;版本是20200…
阅读更多...
动态规划之343 整数拆分（第6道）

动态规划之343 整数拆分（第6道）

题目&#xff1a; 给定一个正整数 n &#xff0c;将其拆分为 k 个 正整数 的和&#xff08; k > 2 &#xff09;&#xff0c;并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例&#xff1a; 解法&#xff1a; 其实可以从1开始遍历 j &#xff0c;然后有两种…
阅读更多...
蓝牙MESH氛围灯智能方案

蓝牙MESH氛围灯智能方案

智能氛围灯可以根据自身照明需要&#xff08;如颜色、温度、亮度和方向等&#xff09;来设定自己喜欢的场景情景照明效果&#xff0c;根据各自要求、场景情况&#xff0c;在不同的空间和时间选择并控制光的亮度、灰度、颜色的变化。便捷的智能手机也提供了更人性化的智能控制渠…
阅读更多...
五路Homekit智能球泡灯

五路Homekit智能球泡灯

五路Homekit智能球泡灯&#xff0c;实际瓦数&#xff1a;9W&#xff0c;E27接口&#xff0c;支持苹果Homekit扫码直连Siri控制&#xff0c;也可在Cozylife app内绑定智能音箱搭配使用&#xff0c;支持包括&#xff08;Alexa、Google Home、小爱音箱、天猫精灵、小度音箱等&…
阅读更多...
LidarPhone攻击将智能吸尘器变成麦克风，小米扫地机器人被黑

LidarPhone攻击将智能吸尘器变成麦克风，小米扫地机器人被黑

LidarPhone攻击的工作原理是将智能真空的激光雷达导航组件转换成一个激光麦克风。 一组学者本周详细介绍了一项新研究&#xff0c;该研究将智能吸尘器改造成能够记录附近对话的麦克风。 这项名为 LidarPhone的技术通过使用真空吸尘器中内置的基于激光雷达的 LiDAR导航组件&…
阅读更多...
最新文章

Copyright @ 2022~2023