点击 -> 这个方式阅读更佳

光线投射算法原理、改进与实现

光线投射算法作为一种直接体绘制技术，其已被广泛应用于医学成像等众多领域。本文通过光线投射法原理、详述其流水线、列举其不足与改进。实验中，通过与面绘制技术
Marching Cube 算法对比，阐述体绘制算法的优点与不足。

关键词： 体绘制；面绘制；光线投射算法； Marching Cube 算法

引言

作为直观显示和分析复杂 3D
体数据的重要工具，体绘制在医学成像、计算流体动力学、有限元模型、地球物理学、遥感技术等领域起着至关重要的作用。一般地，这些大型的体数据来由磁共振成像（MRI）、计算机断层扫描（CT）、卫星成像和声纳等设备采样或通过数值模拟获得。体绘制旨在将三维体数据投影在二维图像平面上，一个体数据集通常组织为由体素（Voxel）组成的
3D 数组。

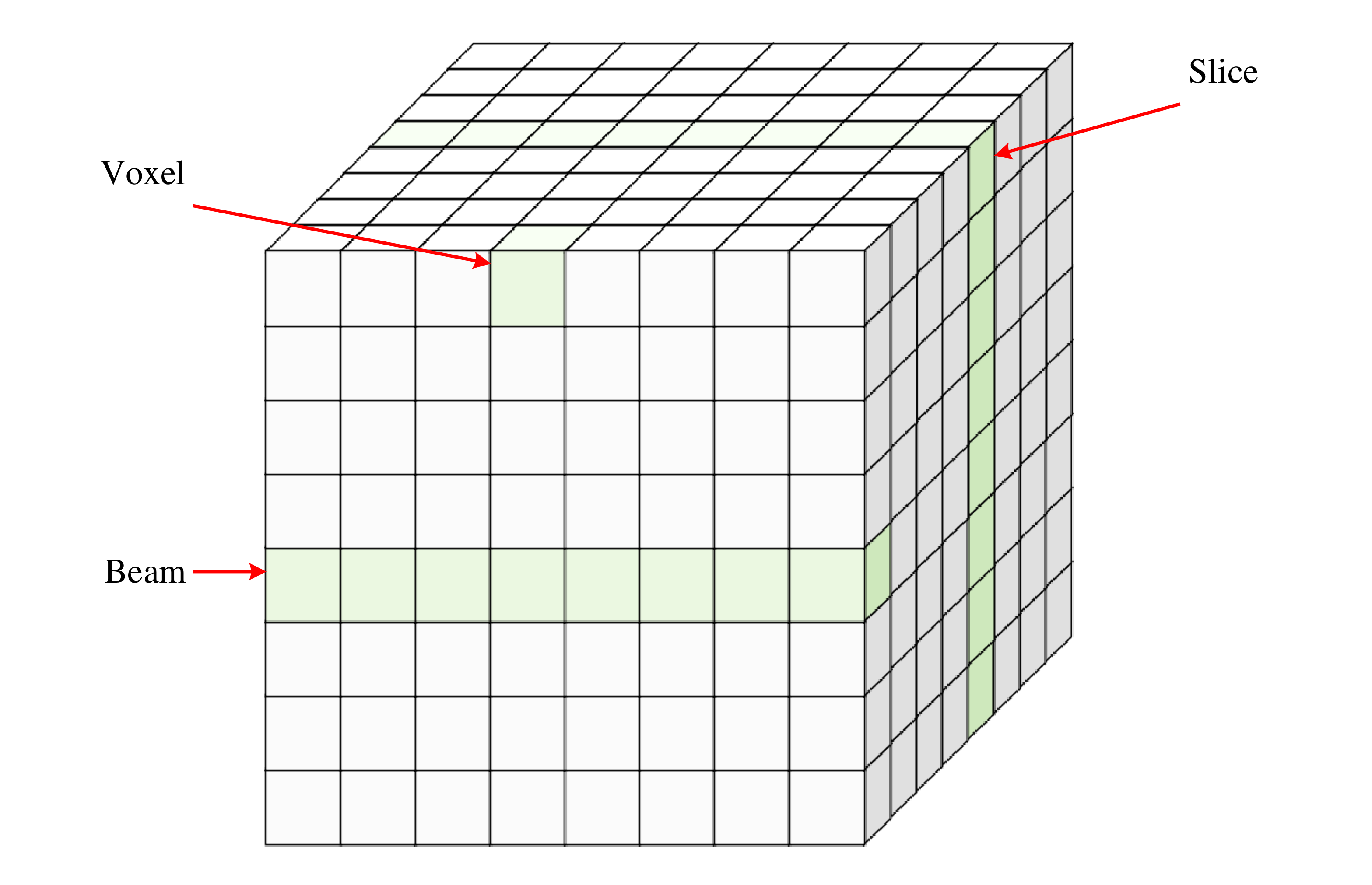
图 1 体数据集组成结构

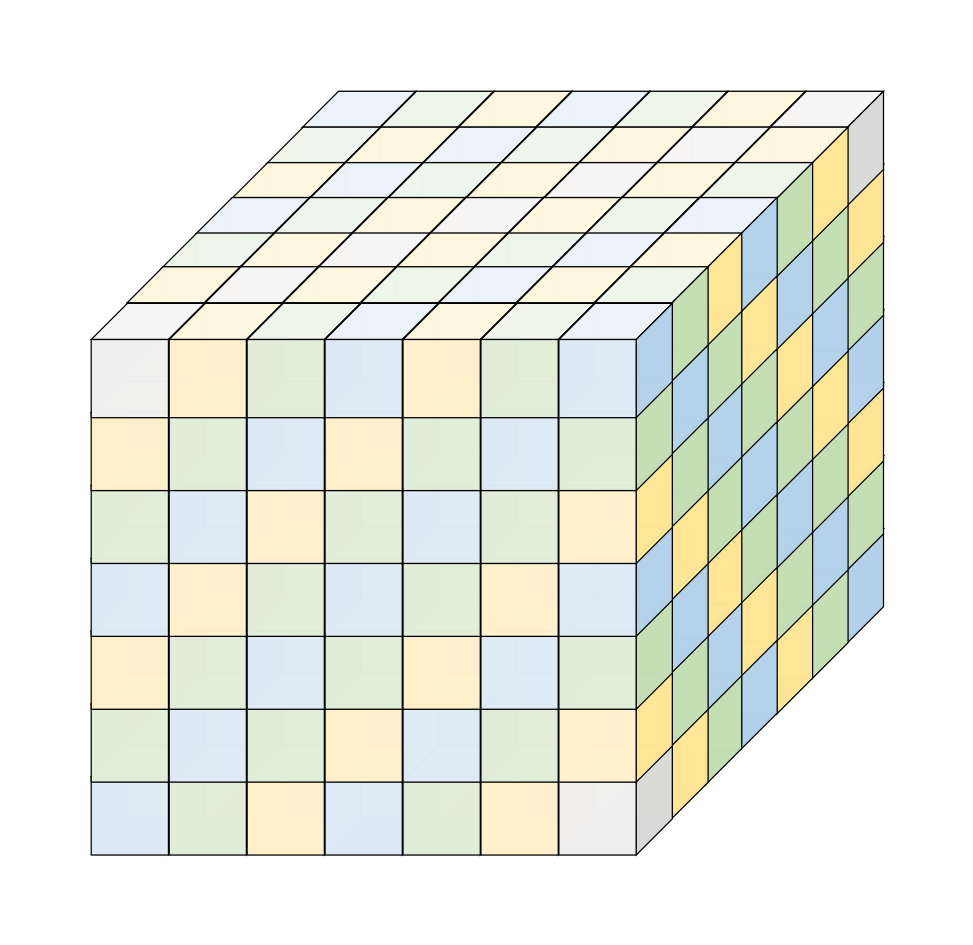
一个体素可以表示各种物理特性（如密度、温度、速度和压力）或其它测量（如面积和体积）。大型体数据可能包含数以亿计的体素，因此需要大量的存储空间。在图
1
中，每一个体素都是均匀等间隔分布的。此外，其它类型的体数据可以分为曲线网格和非结构化网格。前者可以认为是由规则网格产生的，后者由任意形状的单元组成。

体绘制技术可以分为三种，分别是直接体绘制技术（Direct Volume Rendering,
DVR）、间接体绘制技术（Indirect Volume Rendering,
IVR）和最大密度投影法（Maximum Intensity Projection,
MIR）。其中，直接体绘制技术又包括光线投射法（Ray
Casting, RC）、抛雪球法（Splatting）、错切 -
变形算法（Shear-warp）等多种技术。本文旨在介绍光线投射法原理及绘制流水线，回顾其相关研究进展，实现主要的算法。

光线投射算法

光线投射法是一种基于图像序列的直接体绘制技术，由
Levoy 于 1988 年提出。

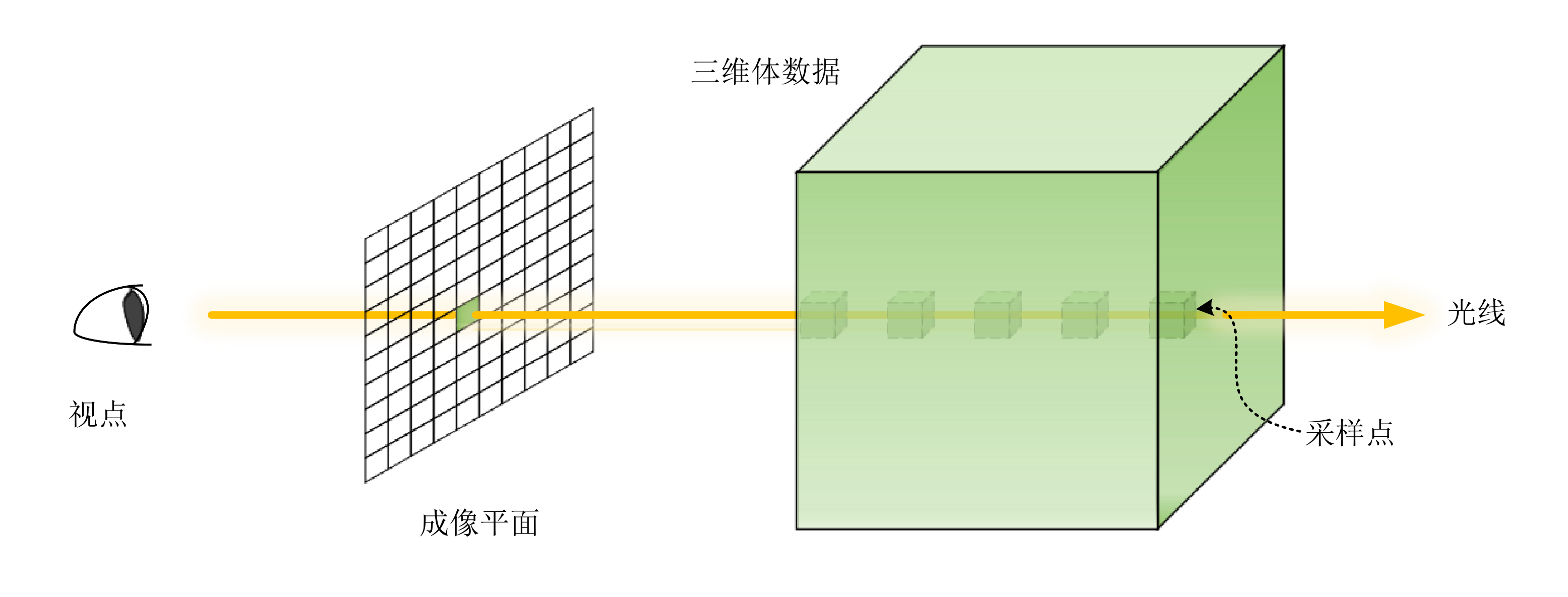
图 2 光线投射算法示意图

光线投射算法原理

与光线跟踪算法（Ray
Tracing）不同，光线投射算法的计算不会停留在物体的表面，而会沿着射线穿过物体内部进行采样，且不会产生二次射线。如图
2
所示，它通过跟踪从视点到物体的射线将 3D
标量数据场中的体数据通过科学计算绘制成 2D 图像。其基本步骤如图
3
所示，即从屏幕上每一个像素点出发，沿着视线方向发射出一条光线，当这条光线穿过体数据时，沿着光线方向等距离采样，利用插值计算出采样点的光学属性（如颜色值和不透明度）；接着按照从前到后（Front-to-back）或从后到前（Back-to-front）的顺序对光线上的采样点进行合成，计算出这条光线对应的屏幕上像素点的颜色值。

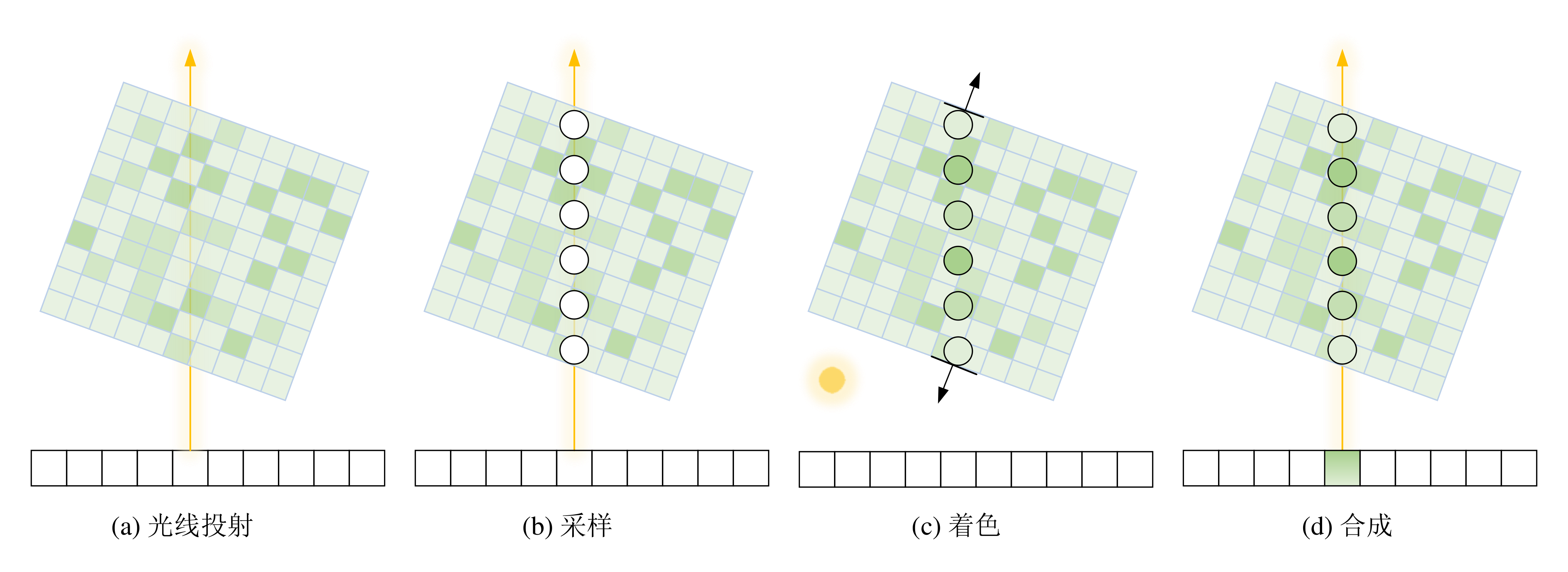
图 3 光线投射算法的四个步骤

光线投射算法流水线

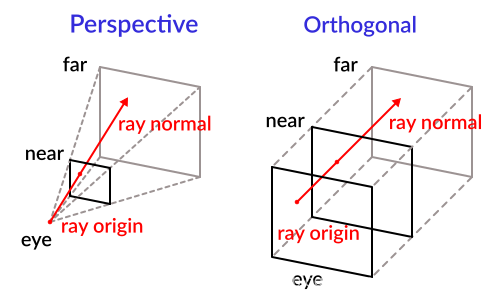
光线投射算法流水线如图 4 所示，其中数据分类主要通过传输函数（Transfer
Function）将体数据中的标量值映射为颜色和不透明度。对体数据的采样需要进行坐标系的变换，因为发射光线起点和方向是在图像空间描述的，而采样则是在物体空间进行的。图像空间到物体空间的转换可以通过旋转和平移操作实现。将光线的描述转换到物体空间后，沿着光线等间隔采样，采样点的颜色和不透明度通过插值获得。最后需要沿着光线对所有采样点的进行合成，得到光线对应的二维屏幕上像素点的颜色。

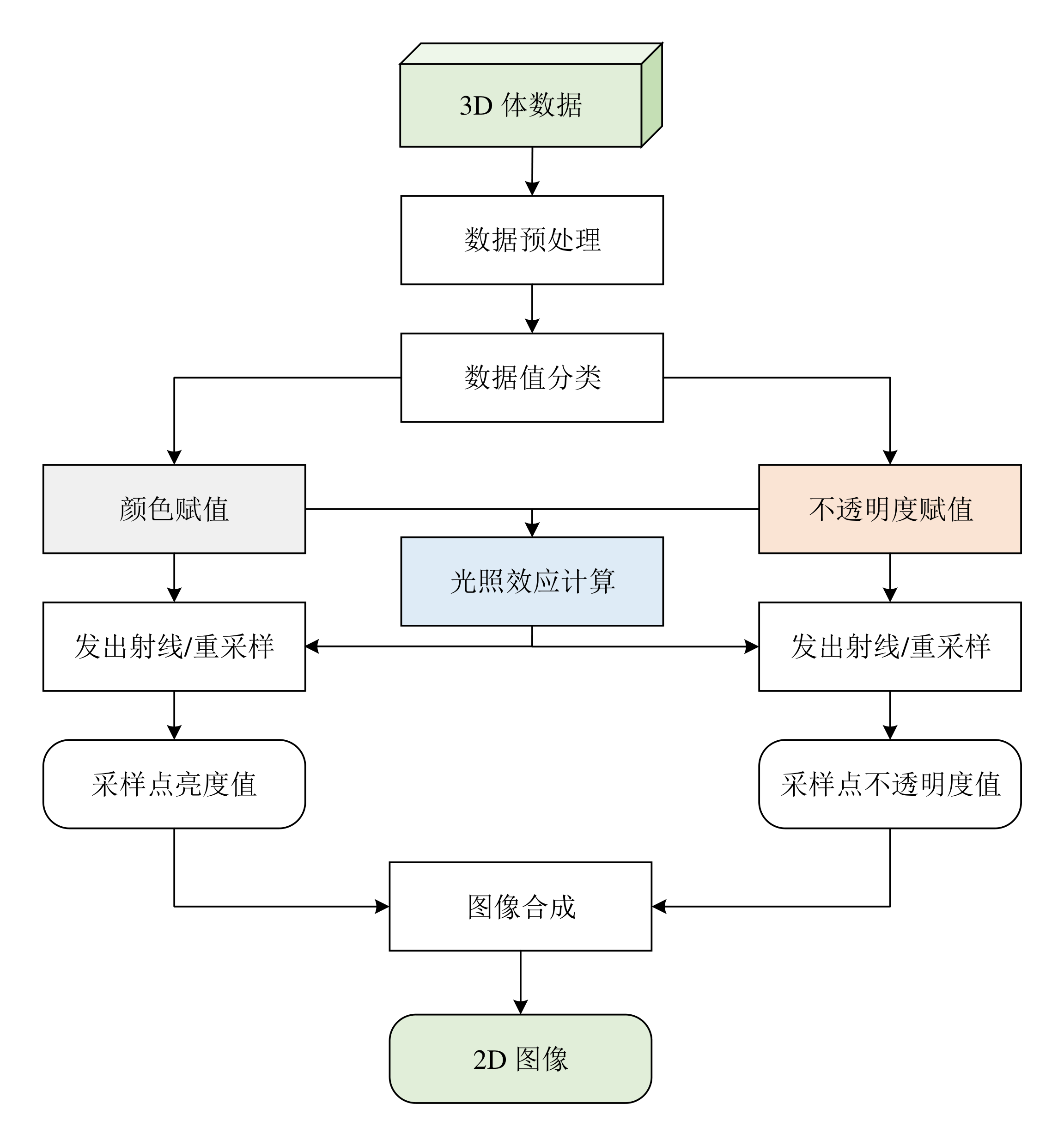
图 4 光线投射算法流水线

一个完整的光线投射系统包括存储组织、射线求交、插值、梯度估计、体素分类、着色与合成。

存储组织

内存系统是可视化体系结构中最重要的组成部分。内存系统包含体数据集，并负责为计算单元提供高带宽的体素值以支持目标帧率。由于体数据集将从不同的视图位置进行可视化，内存系统的吞吐量应该尽可能独立于视图。不管并行处理策略如何，每一种射线投射算法都需要同时访问多个体素。理想情况下，内存系统以无冲突的方式提供这些体素；否则，整个系统的性能可能下降。

如图 5
所示，[memory_a]
分别为四种常见的内存分区方案，用以实现高内存吞吐量。子块划分（图
[memory_a]）将数据集划分为更小的体数据块，每个子块被分配给不同的内存模块。
正交切片划分（图 [memory_b]）将数据集中的每个切片分配给内存模块，每个切片都垂直于数据集的一个轴。在这种分区方案中，内存吞吐量在三个正交视图方向中的两个上最大化。八路交错（Eight-way
Interleaved）存储器系统（图
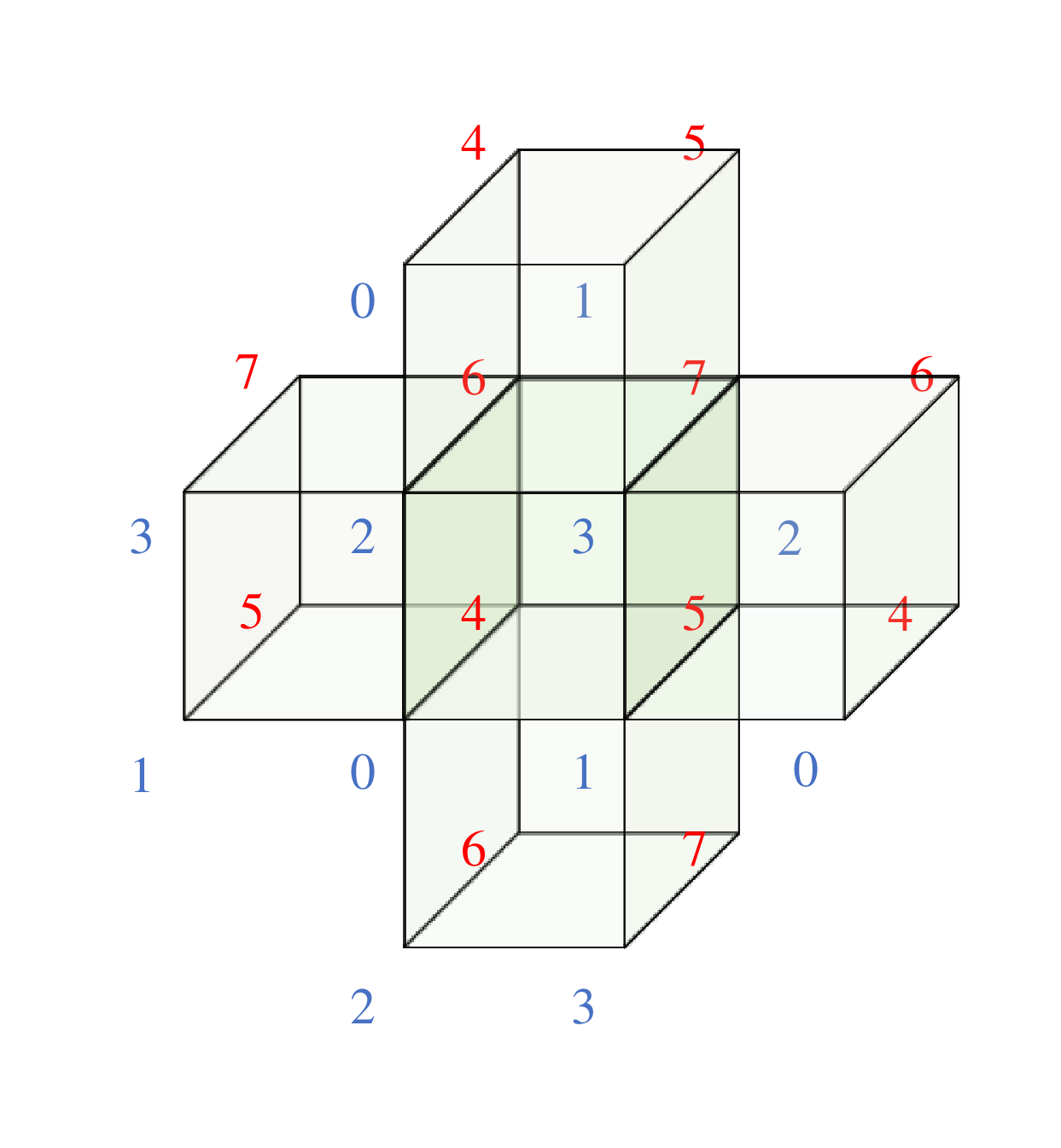
[memory_c]）将每个体素划分成 $2\times2\times2$
块以分隔存储库。八路交错内存分区被限制为 8
个并行内存访问。因此，当需要额外的并行性时，它可以与子块分区结合使用。倾斜（非正交）切片划分方案（图
[memory_d]）将数据集的每个轴成 45
度角的切片分配给内存模块。在这种分区方案中，内存吞吐量在三个正交的查看方向上都是最大的。

<[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MvI32sCS-1608437401370)(https://cdn.jsdelivr.net/gh/ZhouKanglei/jidianxia/2020-12-20/1608430490403-memory_a.png “A”)],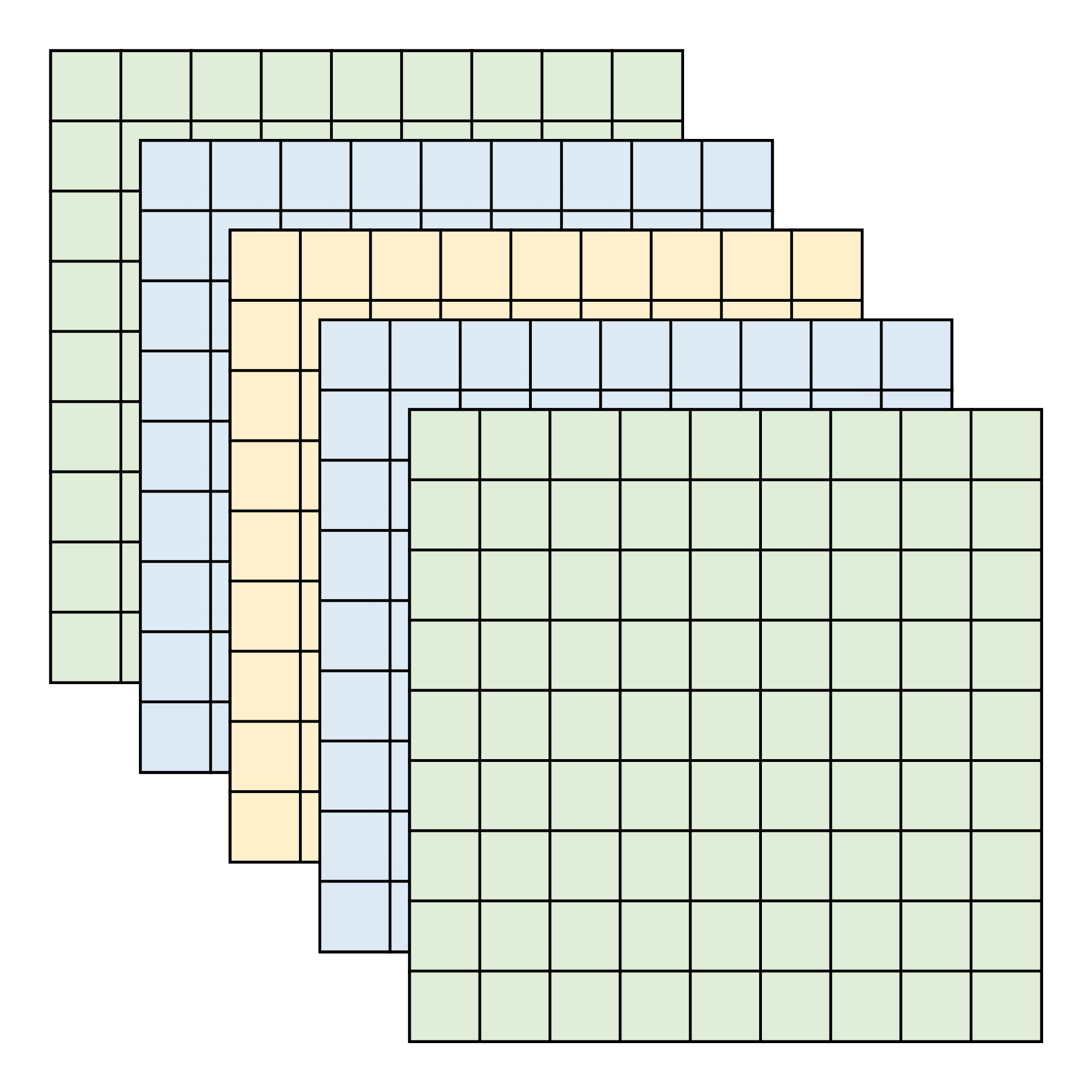 memory_b , memory_c , memory_d >

体绘制体系结构获得的最大性能主要取决于并行度和所使用的内存技术，内存设备一般使用流水线来加速线性访问。

射线求交

光线求交的计算与内存系统设计紧密耦合，并与所使用的光线投射算法类型有关。必须计算光线穿透的每个体素的适当内存地址，这些地址是通过在观测位置和图像平面上的像素之间构建一条射线并通过数据扩展这条射线来计算的，一般的处理策略可能需要并行计算大量内存地址。Yagel1
等
提出用查找表（模板）来减少通过体数据的射线路径所涉及的计算。对于平行投影和混合顺序结构，由于所有光线都有相同的斜率，所以模板只需要在每个投影中生成一次。

三线性插值

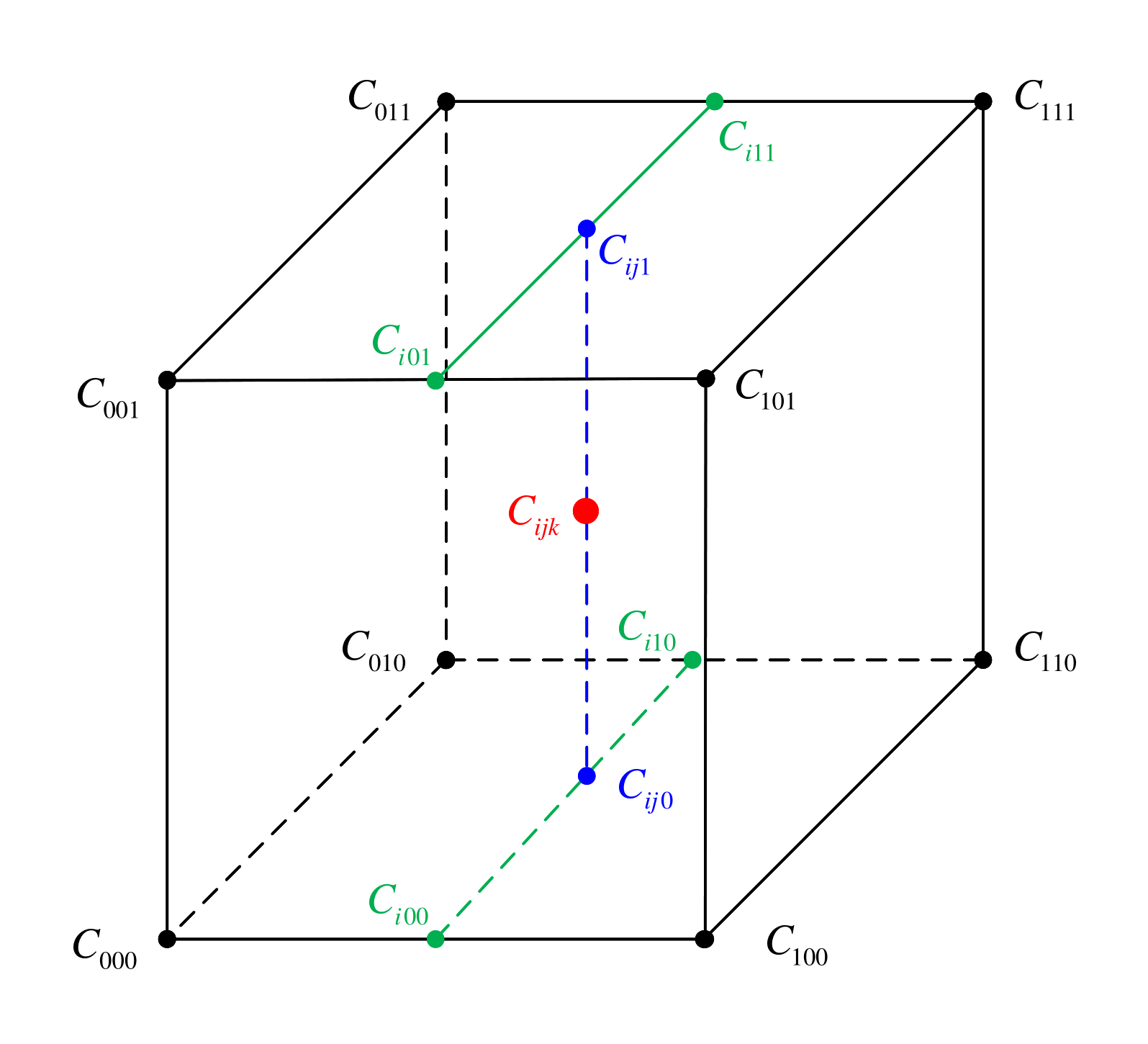
如图 6
所示，通常需要使用三线性插值进行操作。对体素 $C_{ijk}$
的三线性插值与其相邻的 $\times 2 \times 2$ 个体素有关，如下式：
$KaTeX parse error: Undefined control sequence: \label at position 1: \̲l̲a̲b̲e̲l̲{eq:interpolati…$
其中， $\in [0, 1]$ 分别是样本位置在 $x, y, z$
方向上的分数偏移量。由式
(1) 可知，总共需要 24 次乘法，需要 8
个体素值来计算每个重新采样位置。如果重复使用因子，乘法的次数可以减少大约一半。如果大小为
$512\times512\times512$
的体数据中的每个单元中包含一个重样本位置，那么每个投影需要超过 15
亿次乘法操作。而每秒需要多个投影来实现交互投影速率，实时性交互需要具备巨大的计算能力。如果插值权值存储在查找表中，每次操作则只需进行
8
次乘法。高阶插值可以用来改善图像质量，但由于计算成本高，通常不能在硬件上实现。

图 6 三线性插值

梯度估计

梯度估计旨在为分类和着色确定近似表面法线的梯度，高质量的梯度估计需要额外的计算和内存带宽，这可能会影响计算性能和绘制成本。一般来说， $x, y, z$
方向的梯度可以通过中心差分操作计算得到：
$\begin{aligned} G_x =& \frac{C(i+1, j, k) - C(i - 1, j, k)}{\Delta x},\\ G_y =& \frac{C(i, j+1, k) - C(i, j-1, k)}{\Delta y},\\ G_z =& \frac{C(i, j, k+1) - C(i, j, k-1)}{\Delta z}.\end{aligned}$

由于体数据中体素之间往往是等间距分布的，通常可以避免高代价的分割。需要在每个方向上与采样点相邻的两个重采样点使用中心差来计算梯度。一些算法使用更大的体素邻域来生成看起来更平滑或减少时间混叠的图像。
除了梯度向量分量外，还可能需要梯度幅度和归一化梯度向量。梯度也可以在邻近的体素上获得，并进行插值以产生在重新采样位置的梯度。

分类

分类通常在硬件中使用查找表（Look-up
Table）实现，其旨在将体素值映射为颜色和不透明度（ $\alpha \in [0,1]$ ）。查找表的索引通常由样本值或梯度组成，查找结果是样本不透明度和颜色。
在可视化过程中，需要实时修改这些查找表中的信息。
如果体系结构并行处理多个重新采样位置，则必须复制这些查找表以避免争用。

着色

Phong 着色算法
及其改进通常用于体绘制架构的着色子系统中。这个算法需要梯度、光和反射向量来计算每个重新采样位置的阴影颜色。该算涉及计算代价高昂的除法、乘法和取幂运算，这些运算必须在硬件中实现。实际上，着色算法在算术单元中实现以确保准确性
。由于使用 Phong
模型，引入镜面反射、漫反射和环境反射能得到很好的光照效果，在医学上可将各组织器官的性质属性、形状特征及相互之间的层次关系表现出来，从而丰富了图像的信息。

合成

在体绘制中，通常发射 - 吸收（Emission-absorption）光学模型进行渲染。发射 - 吸收模型可以表述为如下方程： $KaTeX parse error: Undefined control sequence: \label at position 1: \̲l̲a̲b̲e̲l̲{eqn_emission_a…$
其中， $I$ 是光线穿过体数据 $a$ 点到 $b$ 点后的光线强度， $q (s)$
表示光线在 $s$ 点处的能量贡献。沿光线的贡献衰减是由光学深度
$\tau = \int \kappa$
进行估计的，其与物体的材质和光的传输有关。一般地，在体绘制中采用传输函数将体数据映射成光学属性
。

根据式
(3)，可得沿光线上各个采样点的颜色合成操作：
$\sum_{i = 1}^n C_i \alpha_i \prod_{j = 1}^{i - 1}(1 - \alpha_j),$
其中， $C$ 为最终的合成颜色， $C_i$ 与 $\alpha_i$ 分别为采样点 $i$
沿入射光线的颜色值和不透明度。进一步，由上式可得由前到后的合成递归方程
$\begin{cases} C'_{i + 1} = C'_i + (1 - \alpha'_i)C_i \alpha_i \\ \alpha'_{i + 1} = \alpha_i + (1 - \alpha_i) \alpha'_i \end{cases}.$
其中， $C'_i$ 为由第 $1$ 个采样点到第 $i$
个采样点由透明度加权累积的颜色值， $\alpha'_i$
为所对应的累积不透明度。特别地， $C'_1 = 0, \alpha'_1 = 0$ 。类似地，由后到前的合成方程为
$\begin{cases} C'_{i + 1} = (1 - \alpha_i)C'_i + C_i \alpha_i \\ \alpha'_{i + 1} = \alpha_i + (1 - \alpha_i) \alpha'_i \end{cases}.$
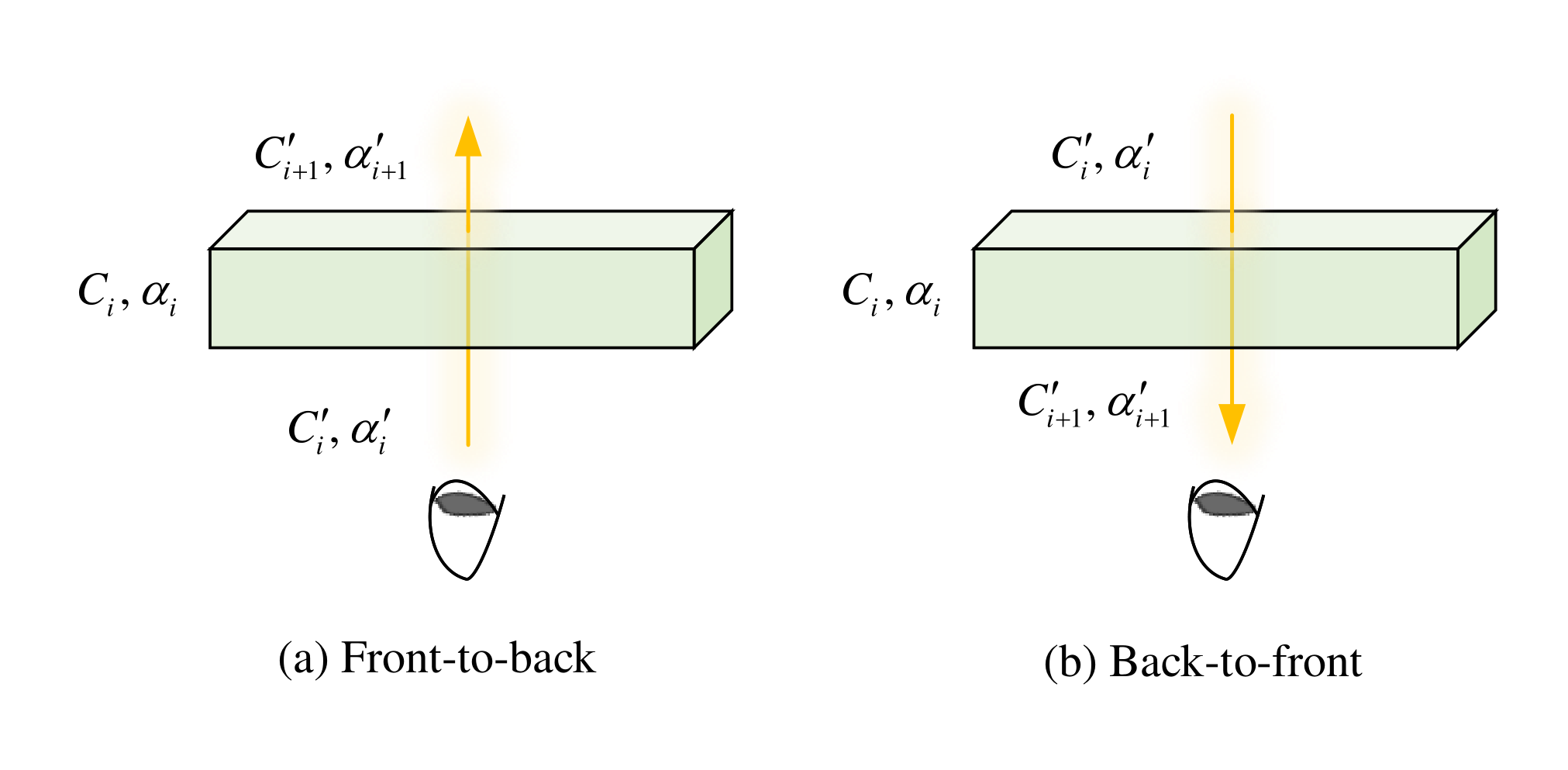
需要注意的是，这种情况不需要计算不透明度 $\alpha$
的合成。此外，图 7 展示了这两种合成方法。

图 7 两种合成方法

光线投射算法不足与改进

传统的射线投影算法虽然能够合成高质量的图像，但存在三个缺点：

一是由于存在大量的体数据，在插值的过程中需要进行大量的加法和乘法运算；
二是采样点确定后，使用三线性插值会影响实时绘制的过程；
三是当观察方向发生变化时，需要重新进行采样，计算量极为庞大。

针对传统的光线投射算法所存在的问题，人们提出了不少优化方法
[@horvat2012ray]，如光线提前终止
[@mora2002new]、利用空间数据结构来跳过无用的体素，如八叉树
[@lim2007half]、金字塔 [@averbuch2010accelerating]、k-d 树
[@horn2007interactive] 等。

实验与结果

本节主要使用 VTK（Visualization Toolkit）包仿真实现面绘制中常用的
MC（Marching
Cube）算法和体绘制中常用的光线投射算法，并给出相应的绘制结果。

实验环境

实验在配置为 Intel® Core™ 7-10510U CPU @ 1.80GHz.2.30 GHz 和 16 GB
memory 的笔记本上使用 Python 3.7 进行，使用 VTK 进行体绘制。

CT 数据

本文中，使用一个含有 245 帧的头骨 CT 数据集 ^1，该数据集的格式为.dcm
文件。

HU（Hounsfield）是放射性密度的一种定量测量指标，由 CT
扫描得到的图像中的像素以相对放射密度显示。根据对应组织的平均衰减来显示区分不同的像素，在
Hounsfield 尺度下衰减的取值在 $-$1024 到超过 3000 之间变化。水的衰减为 0
HU，而空气的衰减为 $-$1000 HU，骨的衰减通常为 +400 HU
或更大，金属植入物通常为 +1000 HU。因此，CT
图像中的像素数据为我们提供了一种直接的方法来大致识别每个像素所属的组织类型。因此，简单地通过阈值化图像到已知范围，我们可以直接从图像中提取给定类型的组织。

提取等值面

为了提取 CT 数据的等值面，首先需要隔离所有骨骼结构，然后使用 MC
算法来创建这些结构的美丽的 3D 网格。

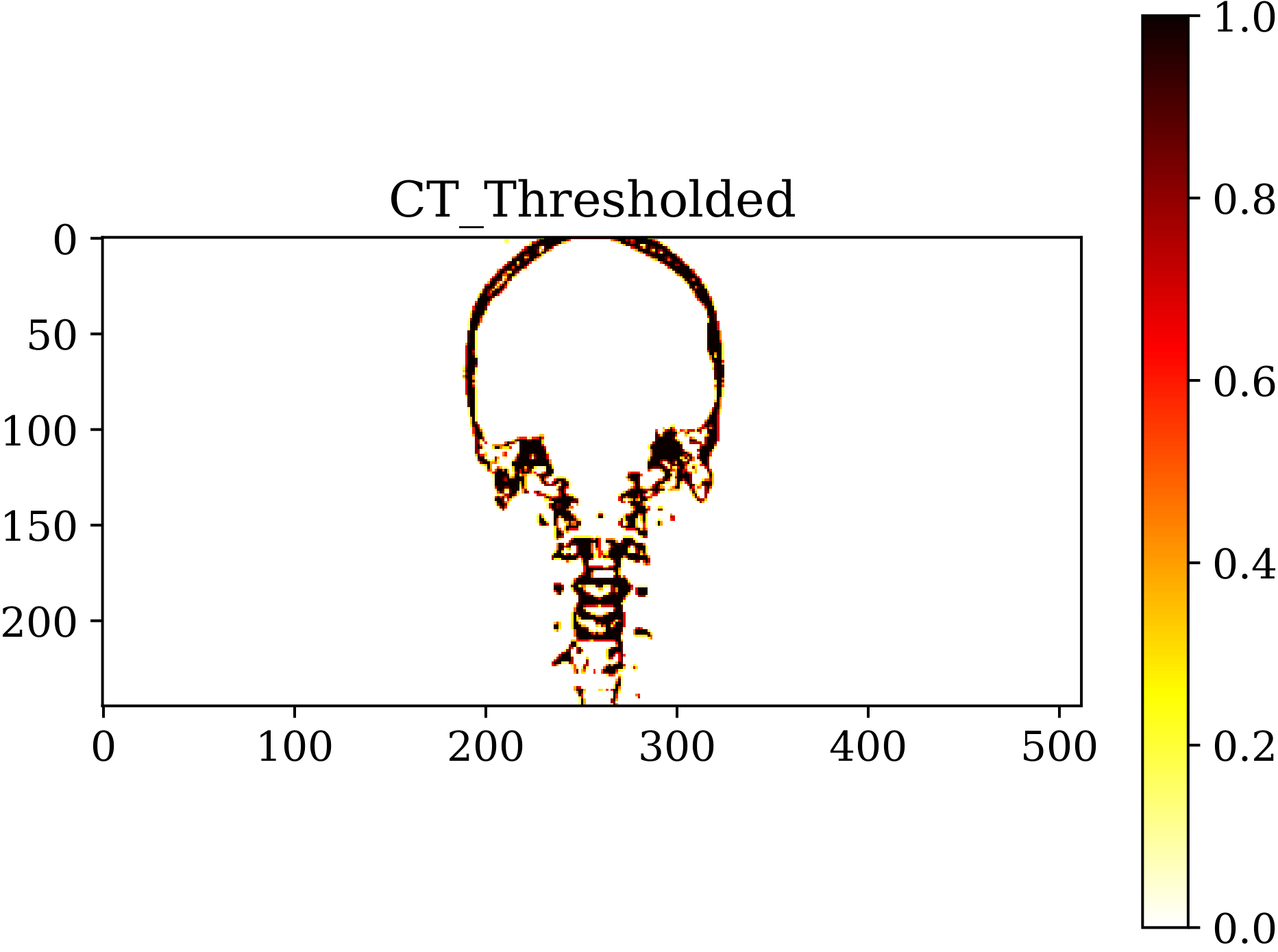
图 [fig:original]
是人头部骨骼原始数据的横截面图，可以看到身体周围的空气的 HU 值为
-1000，软组织如脑物质的 HU 值为 20 - 50，而骨骼结构的 HU 值在 400 HU
以上。因此，我们以 400HU 为阈值来分割骨骼与其它物质，分割后的骨骼切面如
[fig:thresholded] 所示。显而易见，图
[fig:thresholded] 中骨骼得到良好地区分。

< CT_Original , CT_Thresholded >

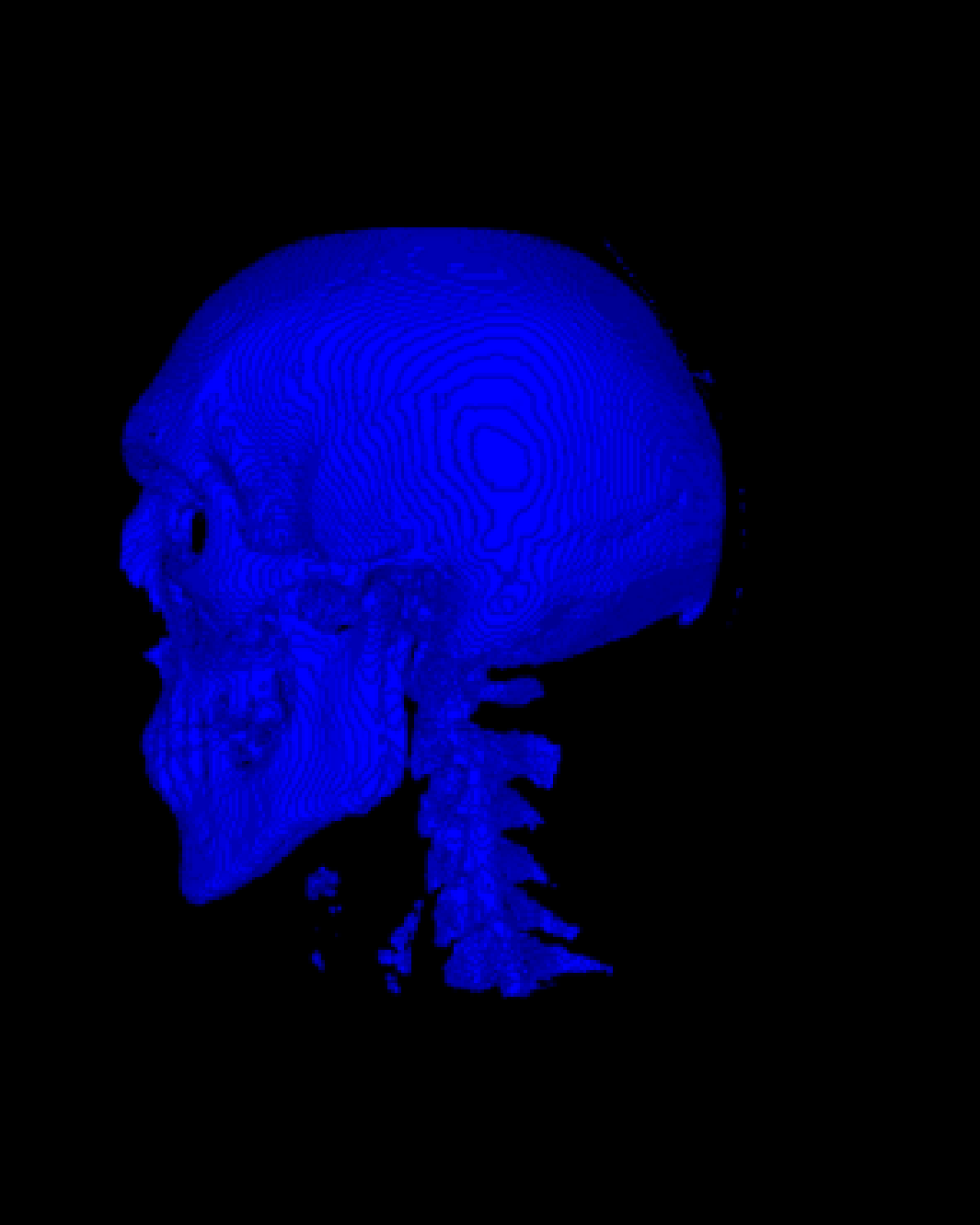
图 [fig:MC] 是使用
MC 算法绘制的等值面结果，[MC_a]
分别为骨骼正面和侧面的视图，可知骨骼和其它物质得到了良好的分割。

<, MC_0 >

光线投射算法

如表 1
所示，通过设置不透明度值来显示体数据内部的不同成分和细节，例如显示人体
CT 图像的不同器官和组织。

  表 1: 传输函数设计#   HU 值      RGB 颜色       不透明度---- ------- ----------------- ----------------1      0     (0.0, 0.0, 0.0)     0.002     500    (1.0, 0.5, 0.3)     0.153    1000    (1.0, 1.0, 0.9)     0.254    1150    (1.0, 1.0, 0.9)     0.85

图
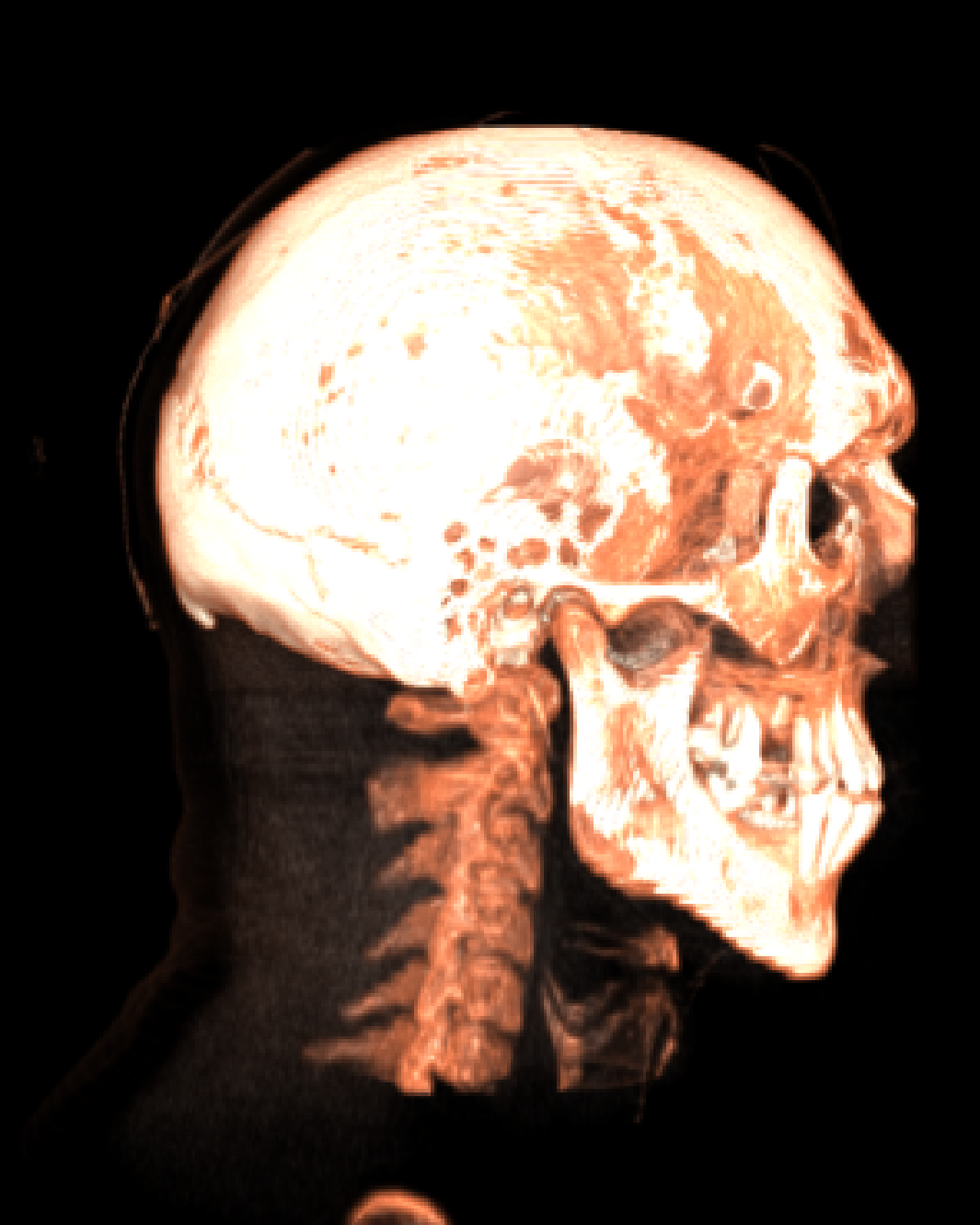
[fig:raycastingrending]
是使用体绘制方法光线投射算法绘制的结果，[ray_a]
分别是人体头部骨骼的正面和侧面视图。显而易见，我们可以发现骨骼周围的一些绘制细节。显而易见，体绘制更能够体现出复杂体数据的细节结构，有利于进行细节分析、展示效果更佳。

< RC_bones_0 ,>

面绘制与体绘制

在面绘制中，采用的渲染技术都是几何渲染，即通过绘制几何图元（顶点、线段、面片等）来渲染数据。体绘制技术是由离散的三维数据场直接产生对应二维图像的一种绘制技术，其渲染线和几何渲染线的组成是基本一致的。
体绘制则是直接在原图上进行绘制，内容需求较面绘制小。每切换一个视角需要重新对所有的像素点进行颜色和透明度计算，需要时间比面绘制长。

和等值面方法不同，在这一过程中并不需要产生中间几何图元。体绘制技术的优点是能从所产生的图像中观察到三维数据场的整体和全貌，而不只是显示出人们感兴趣的等值面；同时，体绘制也易于进行并行处理。

小结

本文概述了直接体绘制中的光线投射算法的原理，详细阐述了光线投射算法的流水线，指出传统的光线投射算法存在的问题并简要列举了相应的改进措施。分别对
CT 数据集使用 MC 算法和 RC
算法进行面绘制和体绘制，对比了体绘制和面绘制的异同。与面绘制算法相比，体绘制有助于探索物体的内部结构，可以描述非常定形的物体；缺点是数据存储量大，计算时间较长。