一、容斥原理

1、定理内容

我们在高中阶段都学过韦恩图，韦恩图其实就是用来描述集合与集合之间的关系的。

我们看下面的图：
请添加图片描述
这道题的话，我们首先将三个圆圈加在一起，但是叶子形状的部分会被我们重复加了两遍，所以我们要减去。但是三个叶子形状的中间也会有交叉的部分。所以这个部分又被我们减少了三次。所以我们还要再加上一次中间部分。

因此，就出现了我们图中的红色式子。

因此，我们总结出了一个规律。如果我们求的是奇数个集合的合并，那么我们就要加上。如果是偶数个集合的合并，我们就要减去。

那么我们从这个特殊的例子推广到一般情况，就会得到如下公式：
请添加图片描述
而这个式子就是我们的容斥原理。

那么容斥原理的时间复杂度是多少呢？

我们可以看作我们的前面有 $n$ 个集合 $S$ ，那么我们从中选出1个集合就是 $C_n^1$ 。
选出任意两个集合的交集，就是 $C_n^2$

那么依次类推：

我们选出所有集合所需的情况就是：

$C_n^1+C_n^2+C_n^3+...+C_n^n$

而根据我们高中的知识：
$C_n^0+C_n^1+C_n^2+C_n^3+...+C_n^n=2^n$

那么我们选出所有情况来运用容斥原理计算的次数就是：

$C_n^1+C_n^2+C_n^3+...+C_n^n=2^n-1$

时间复杂度就是 $O(2^n)$

二、代码模板

1、问题

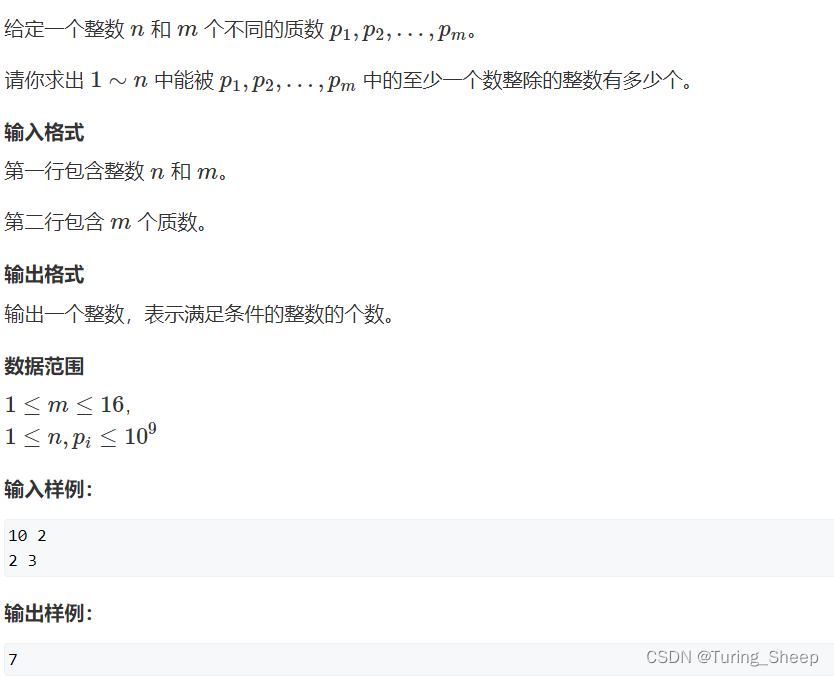
在这里插入图片描述

这道题可以转化成下面的图片：

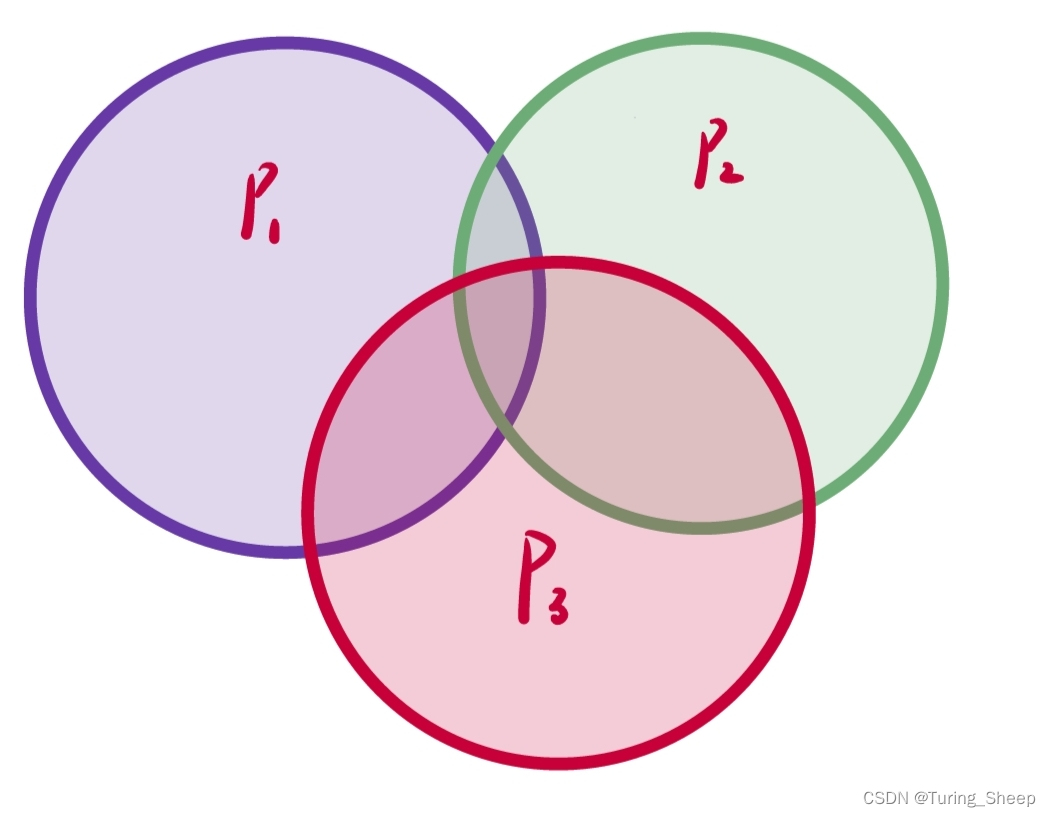
请添加图片描述
紫色圈代表能够被p1整除的，绿色圈代表能被p2整除的，依此类推。题目中就是让我求上图中的元素个数。

如果我们只是单纯的把被某个数整除的数字个数加起来的话，中间一定会有重复的。因此，我们需要根据容斥原理来求。

利用容斥原理的话，我们有以下几个问题：

（1）如何求出能够被整除的个数？

其实很简单，能被 $p_1$ 整除的个数是 $[Np1][\frac{N}{p_1}]$ ，

中间的交集的话，我们以能够被 $p_1$ 或者 $p_2$ 为例。我们只需要求 $[Np1∗p2][\frac{N}{p_1*p_2}]$

依次类推。

（2）如何枚举出 $2^n-1$ 种情况？

那么这个枚举的话，可以采用二进制的思想，我们的情况一共是 $2^n-1$ 种，我们将其转化为二进制的话，（以n=3）为例：

$2^3-1=111$

每一位代表一个集合，此时三位都是1，说明我们要求三个集合的交集。

那么如果是 $101$ ，就代表我们要求第一个集合和第三个集合的交集。

而我们的所有情况无非就是从 $001 - 111$ ，换算为十进制的话，我们就是要枚举从 $1$ 到 $2^n-1$ 。这中间的每个数字的二进制位都代表着一种情况。

当上述两个问题解决之后，我们就可以套用容斥原理的公式了。

2、代码实现：

#include<iostream>
using namespace std;
typedef long long LL;
const int N=20;
int p[N];
int main()
{int n,m,res=0;cin>>n>>m;//读取除数for(int i=0;i<m;i++)scanf("%d",p+i);//枚举情况for(int i=1;i<1<<m;i++){//t用来记录结果，s用来记录集合的个数int t=1,s=0;//枚举情况i的二进制位for(int j=0;j<m;j++){if(i>>j&1)//如果这一位是1，那么就让该位对应的集合参与运算{if((LL)t*p[j]>n)//如果几个数的积，已经大于了n，那么这种情况不存在。{t=0;//如果不存在了，就直接扔掉就好了。break;}t*=p[j];//乘上该集合所对的除数s++;//记录参与的集合个数}}if(t){//使用容斥原理：if(s%2)res+=n/t;//如果集合是奇数就加上else res-=n/t;//如果集合是偶数就减去}}cout<<res<<endl;
}