一、Attention原理
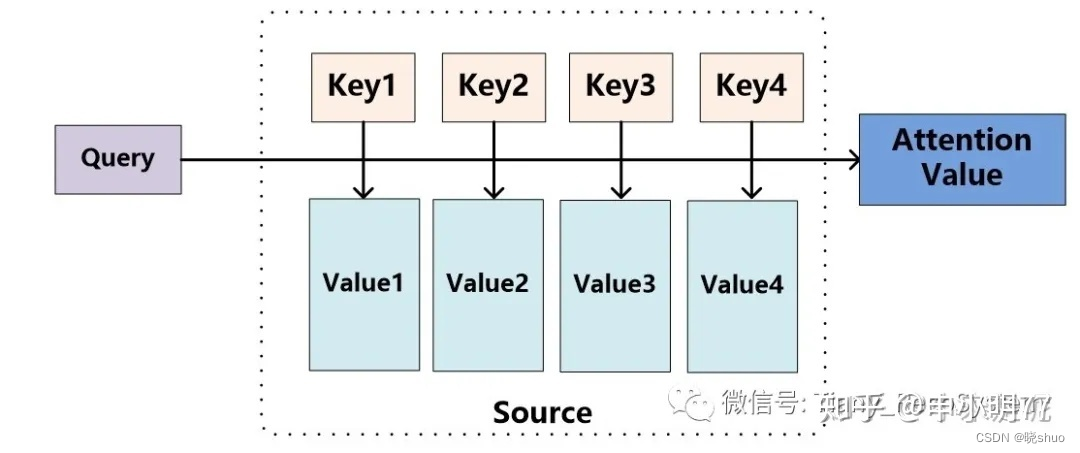
将 S o u r c e Source Source中的构成元素想象成是由一系列的 < K e y , V a l u e > <Key,Value> <Key,Value>数据对构成,此时给定 T a r g e t Target Target中的某个元素 Q u e r y Query Query,通过计算 Q u e r y Query Query和各个 K e y Key Key的相似性或者相关性,得到每个 K e y Key Key对应 V a l u e Value Value的权重系数,然后对 V a l u e Value Value进行加权求和,即得到了最终的 A t t e n t i o n Attention Attention数值。所以本质上 A t t e n t i o n Attention Attention机制是对 S o u r c e Source Source中元素的 V a l u e Value Value值进行加权求和,而 Q u e r y Query Query和 K e y Key Key用来计算对应 V a l u e Value Value的权重系数。即可以将其本质思想改写为如下公式:
A t t e n t i o n ( Q u e r y , S o u r c e ) = ∑ i = 1 L x S i m i l a r i t y ( Q u e r y , K e y i ) ∗ V a l u e i Attention(Query,Source)=\sum_{i=1}^{L_{x}}Similarity(Query,Key_{i})*Value_{i} Attention(Query,Source)=i=1∑LxSimilarity(Query,Keyi)∗Valuei
二、向量内积
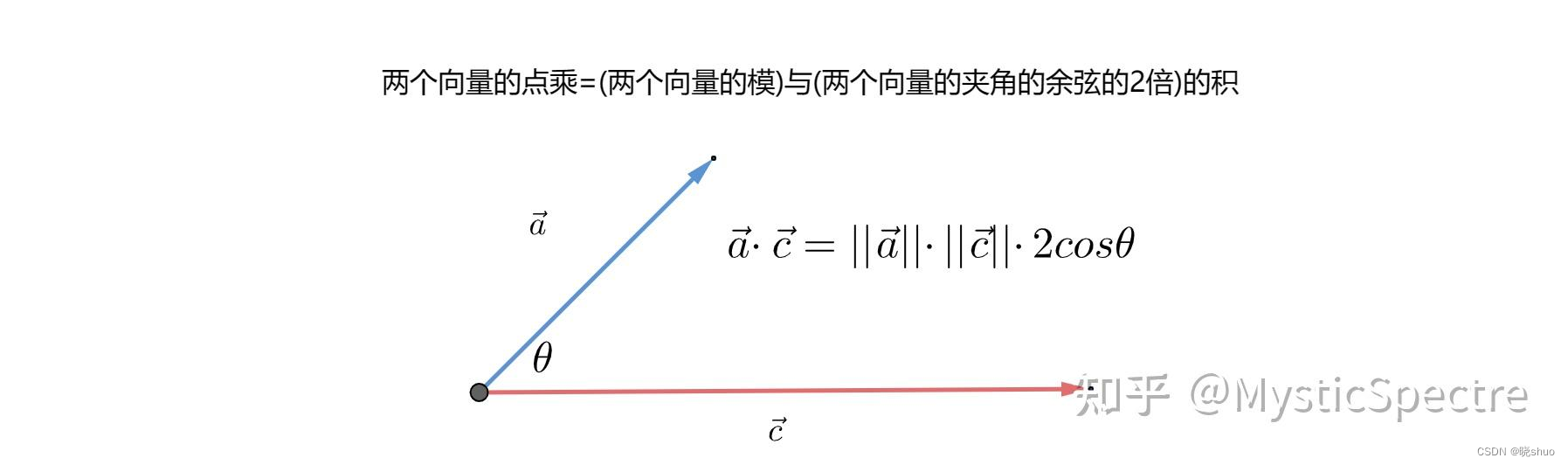
向量内积又叫向量点乘,公式如下:
a ⃗ ⋅ c ⃗ = ∥ a ⃗ ∥ × ∥ c ⃗ ∥ × c o s θ \vec{a}\cdot \vec{c}=\parallel\vec{a}\parallel\times \parallel\vec{c}\parallel \times cos \theta a⋅c=∥a∥×∥c∥×cosθ
向量内积的求导公式如下:
∂ ( x ˉ ⋅ w ˉ ) ∂ w ˉ = x ˉ T \frac{\partial(\bar{x}\cdot \bar{w})}{\partial \bar{w}}=\bar{x}^{T} ∂wˉ∂(xˉ⋅wˉ)=xˉT
三、Transformer中的Scaled Dot-Product Attention
公式如下:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V Attention(Q,K,V)=softmax(dkQKT)V
对一组key-value对和n个query,可以使用两次矩阵乘法,并行的计算里面的每个元素。