优美的曲线-译

news/2024/12/21 4:21:10/

来源：Some equations that describe beautiful curves

链接：

1. iviveros.github.io/param-eq/#introduction

2. mathworld.wolfram.com/ButterflyCurve.html

介绍
在本文中，我收集了一些生成我喜欢的曲线的方程式。
如果你喜欢数学艺术，我建议你看看哈米德·纳德里·叶加内的作品，他根据数学概念构建了美丽的图像。
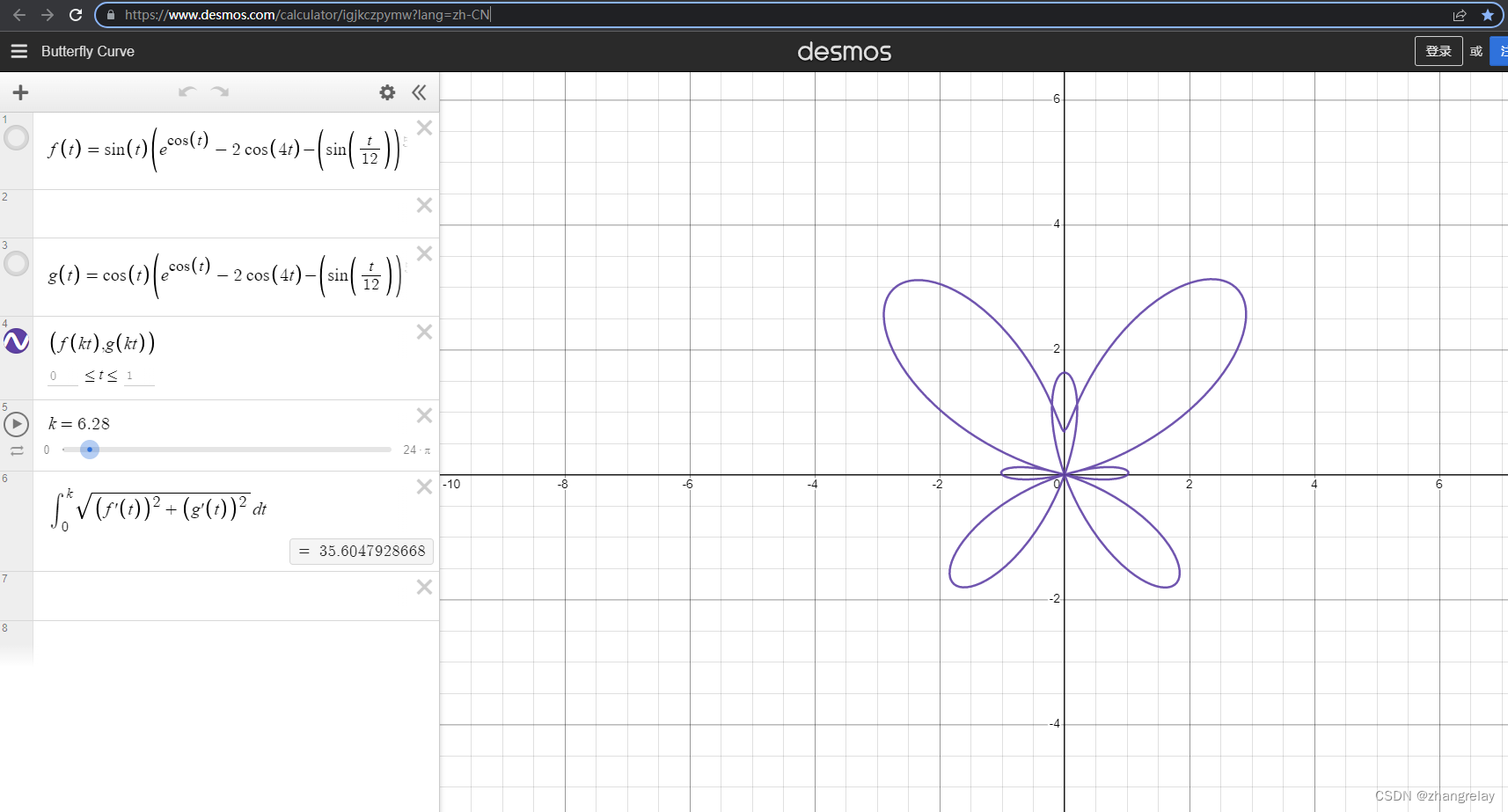
蝴蝶曲线
Fay（1989）在论文中定义了蝶形曲线。该曲线根据以下参数方程进行描述：

~~x=sin(t)(ecos(t)−2cos(4t)−sin5(t12))~~

~~y=cos(t)(ecos(t)−2cos(4t)−sin5(t12))~~

~~t is in the range: [0,12π]~~

$x=sin(t)\Big(e^{cos(t)}-2 \, cos(4t)-sin^5\big(\frac{t}{12}\big)\Big)$

$y=cos(t)\Big(e^{cos(t)}-2 \,cos(4t)-sin^5\big(\frac{t}{12}\big)\Big)$

注意，t的范围。

绘制曲线网站：www.desmos.com/calculator/igjkczpymw?lang=zh-CN

# the function butterfly generates a data frame
# by evaluating the parametric equations that
# define the rose curve in the range of 0 to 12pi
butterfly <- function(n=1000){data.frame(t = seq(0,12*pi,length.out = n)) %>%mutate(x = sin(t)*(exp(cos(t))-2*cos(4*t)-(sin(t/12))^5),y = cos(t)*(exp(cos(t))-2*cos(4*t)-(sin(t/12))^5))
}

玫瑰
该曲线由以下参数方程描述：

$x=cos(k \, \theta) \, cos(\theta)$

$y=cos(k \, \theta) \, sin(\theta)$

n和d值组合的玫瑰曲线，定义k=n/d。
n和d跨度在[1，10]范围内

rose_curve <- function(n,d) {data.frame(theta = seq(0, 32*pi,pi/180)) %>%mutate(x = cos(n/d*theta)*cos(theta),y = cos(n/d*theta)*sin(theta)) %>%select(x, y)
}

次摆线
有关内摆线的详细信息，请参阅Wolfram MathWorld文章。
当x（0）=a时，定义内摆线的参数方程为：

$x=(a-b)\,cos(t) + b\,cos\big(\frac{a-b}{b}t\big)$

$y=(a-b)\,sin(t) - b\,sin\big(\frac{a-b}{b}t\big)$

hypocycloid <- function(n = 200, a_inc,b_inc,t_inc){a0 = seq(1,n)b0 = seq(1,n)t0 = seq(0,n-1)for (i in 2:n) {a0[i]=a0[i-1]+a_incb0[i]=b0[i-1]+b_inct0[i]=t0[i-1]+t_inc}data.frame(a0,b0,t0) %>%mutate(  x0 = (a0 - b0)*cos(t0) + b0 * cos((a0/b0-1)*t0),y0 = (a0 - b0)*sin(t0) - b0 * sin((a0/b0-1)*t0),x1 = c(x0[2:n],x0[1]),y1 = c(y0[2:n],y0[1])) %>%select(x0,y0,x1,y1,t0)
}

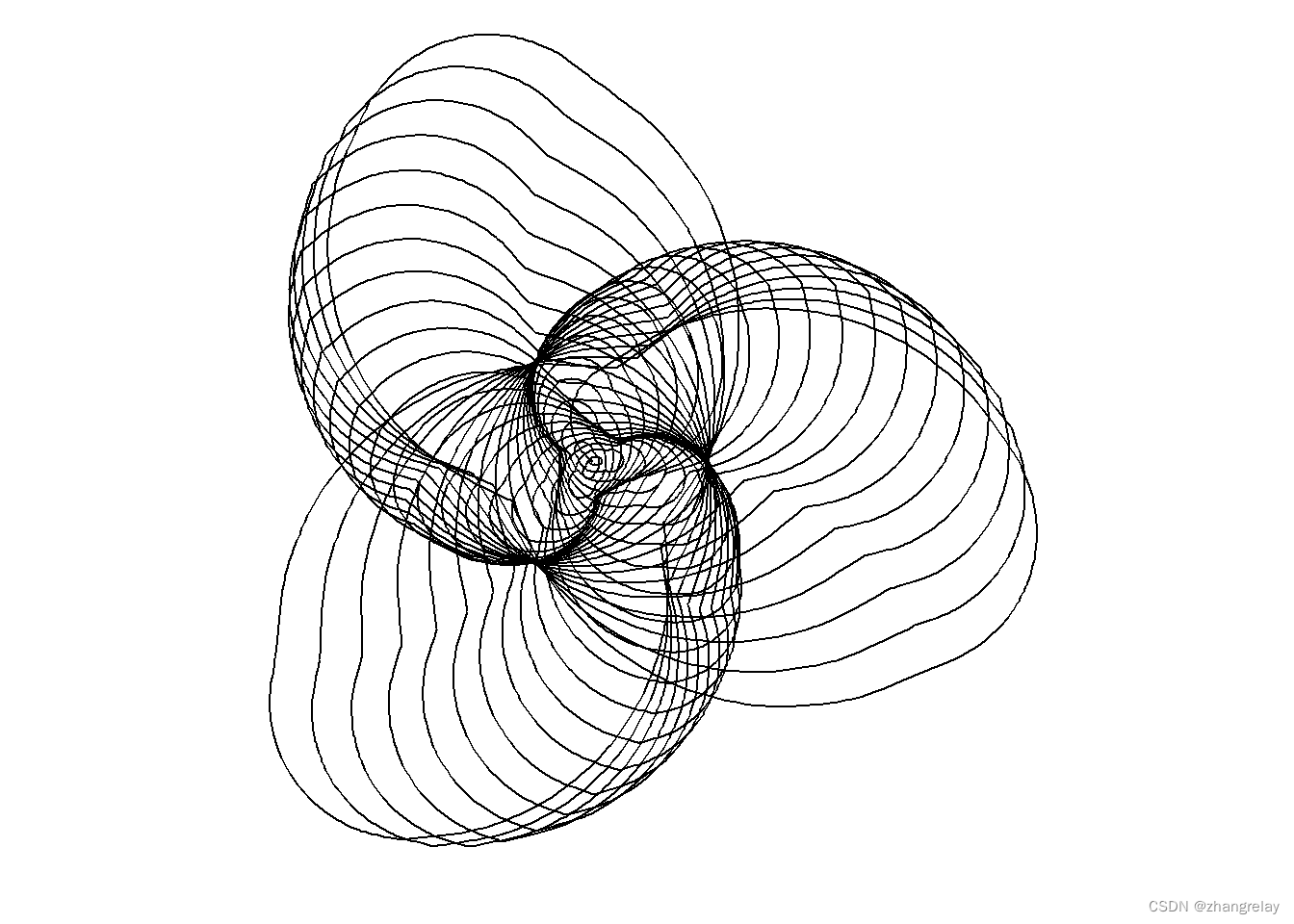
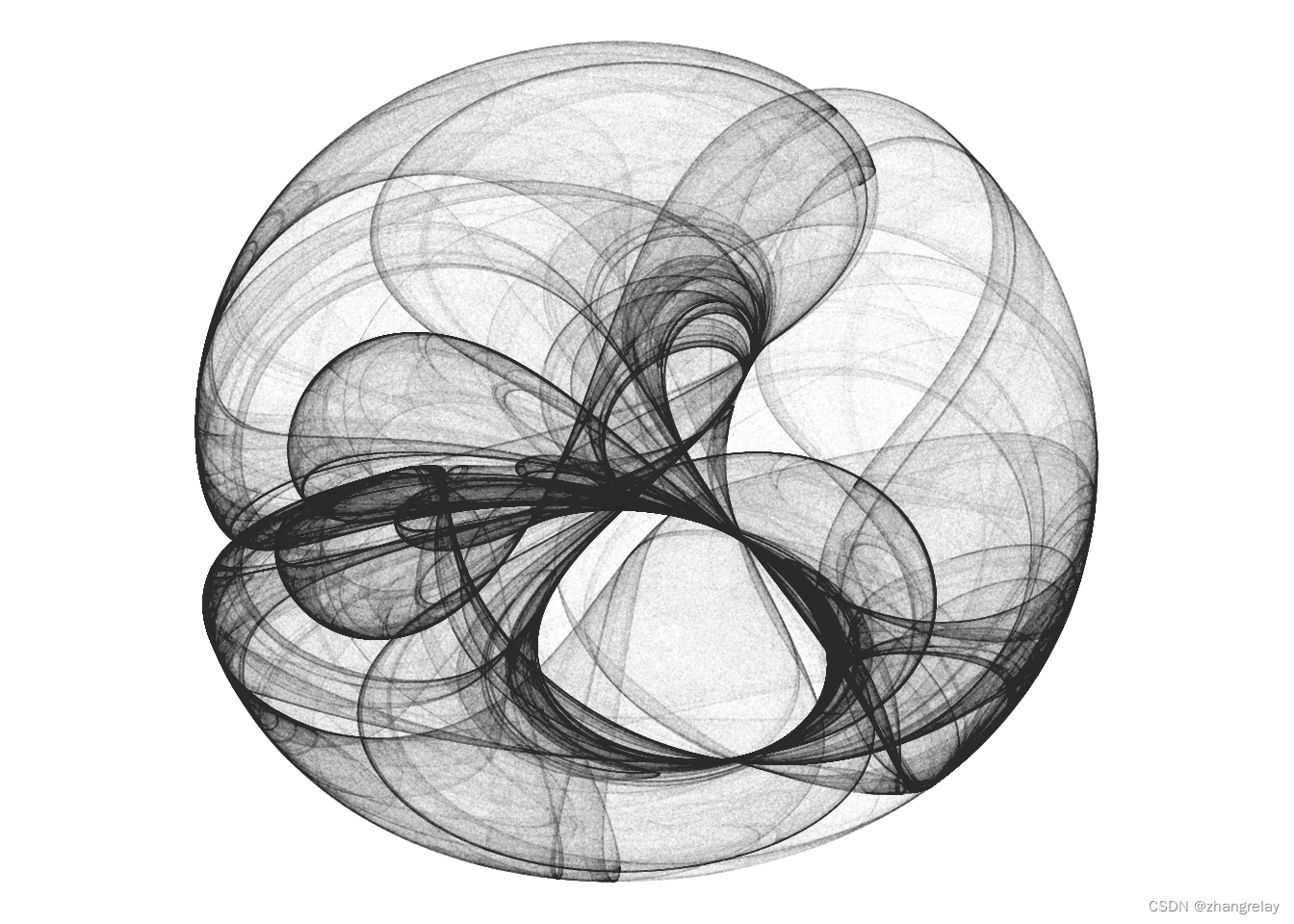
Clifford吸引子
Clifford吸引子由以下方程定义：
~~xn+1=sin（ayn）+ccos（axn）~~
~~yn+1=sin（bxn）+dcos（byn）~~

$x_{n+1}=sin(a\,y_n) + c\, cos(a\,x_n)$

$y_{n+1}=sin(b\,x_n) + d\, cos(b\,y_n)$

上述方程确定了从点（x0，y0）开始并根据参数a、b、c和d的粒子离散步的（X，Y）位置。
功能选择基于Antonio Sánchez Chinchón的实现。唯一的区别是拾音器是基于R的，而Sánchez Chinchón通过rcpp包在C++中定义了他的功能。

# n is set to 1M
# a, b, c and d are the parameters of the equations
pickover <- function(n=10000000,a,b,c,d){x <- vector("numeric", n)y <- vector("numeric", n)x[1] <- 0y[1] <- 0for(i in 2:n) {x[i] <- sin(a * y[i-1]) + c * cos(a * x[i-1])y[i] <- sin(b * x[i-1]) + d * cos(b * y[i-1])}df <- data.frame(x = x, y = y)
}