1. 前言

限于作者能力水平，本文可能存在谬误，因此而给读者带来的损失，作者不做任何承诺。

2 为什么需要内存一致性(Memory Consistency)模型

从硬件的角度来看，最初对内存的访问过程大概是这样：

CPU <--> 内存

相对于 CPU 的执行频率，直接访问内存速度较慢。于是引入存储速度比内存更快但更贵更小容量的 CPU cache ，用于缓存最近访问的内存数据，硬件拓扑结构如下图（不考虑多级 cache 情形）：

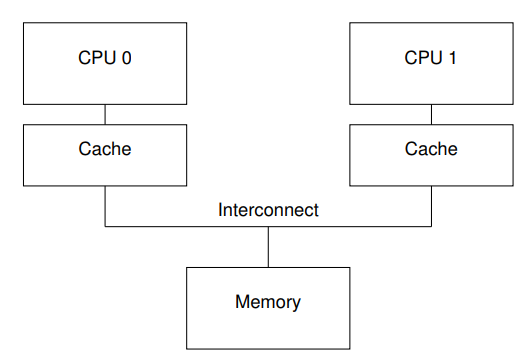
于是访问内存的过程变成了这样：

1. cahce 命中，直接从 cache 中读取CPU <--> CPU cache
2. cahce 未命中，从内存加载到 cache ，再从 cache 读取CPU <--> CPU cache <--> 内存

有了 CPU cache，速度上得到了很大提升，但人的追求永无止境，为了更快的速度，在 CPU 和 cache 之间， 又加入了更快更贵更小容量的 store buffer 存储。此时硬件拓扑如下：

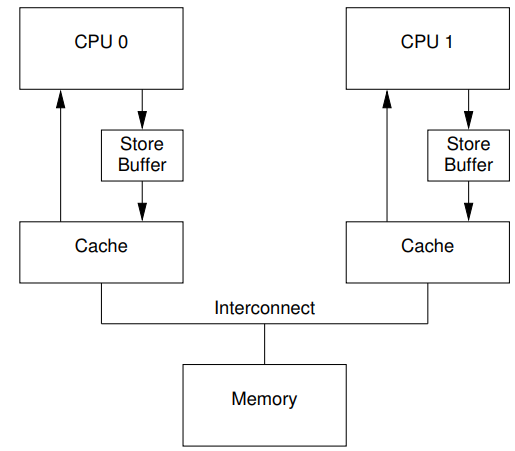
在有 store buffer 缓存的情形下，写操作数据写入到 store buffer ，在需要的时候再写入到 cache 。
说了这么多，这和引入内存一致性模型有什么关系？来看一个例子：

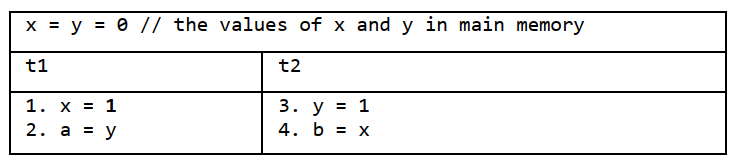
其中：

. t1 和 t2 代表两个线程，t1 绑定在 CPU 1 上运行，t2 绑定在 CPU 2 上运行；
. 变量 x 和 y 被两个线程共享，初始值为 0。

那么，最终 a 和 b 的值分别是多少呢？在没有引入内存一致性模型前，对这个问题无法讨论，接下来一一介绍几个常见的内存一致性(Memory Consistency)模型。我们将在 TSO 模型 下讨论这个例子。

3. 什么是内存一致性(Memory Consistency)模型

内存一致性模型(Memory Consistency) 包括 硬件层面的模型（由硬件负责）和 语言的内存模型（由编译器负责，如 DRFx）。本文只讨论 硬件层面的模型，后文出现的 内存一致性模型(Memory Consistency) 专指 硬件层面的模型。
内存一致性(Memory Consistency)模型就是对内存读写(load/store)的以下4种顺序进行定义：

store-load
store-store
load-load
load-store

以 store-load 来举例，就是说代码中有两条指令，在顺序上，第1条时写指令(store)，第2条是读指令(load)，内存一致性(Memory Consistency)模型，就是从硬件设计上，是否保证严格按代码中这两条指令的先后顺序进行内存访问。这是什么意思？譬如在后面提到的 TSO(Total Store Order) 模型上下文，可能的执行情况是这样：第1条写指令(store)，执行在 CPU 0 上，将变量 var 数据写入到 store buffer ；第2条读指令(load)，执行在 CPU 1 上，它去读取变量 var 的数据，而这时候变量 var 的最新数据在 CPU 0 的 store buffer 里面，CPU 1 是无法看到 CPU 0 的 store buffer 的，所以读取的就不是变量 var 的最新值，这看起来，就是发生了 store-load 乱序（注意，是发生在不同 CPU 间）。

4. 各种内存一致性(Memory Consistency)模型

4.1 顺序一致性(SC: Sequential Consistency)模型

所有 章节 3 中提到的4种存储操作，严格按照代码顺序执行。在 顺序一致性(SC: Sequential Consistency)模型 下， 章节 3 例子中最终 a = 1, b = 1。

4.2 完全存储定序(TSO: Total Store Order)模型

在 完全存储定序(TSO: Total Store Order)模型 下，写操作(store) 不会将数据立即写入内存，而是先写到按严格先入先出(FIFO)的 store buffer 队列。
章节 3 中提到的4种存储操作，允许 store-load 的写读存储操作乱序，其它操作保序。但要了解的是，这种乱序是指不同 CPU 之间的乱序：因为数据写到 CPU 自身的 store buffer ，而 直到将 CPU 自身 store buffer 中的数据刷出之前， CPU 自身 store buffer 中的数据不会被其它 CPU 看到；但是如果是 CPU 自身发起的读操作(load)，则是可以看到写入到 store buffer 的最新值的。CPU 何时将 store buffer 中的数据刷出，从我目前了解的资料，都没有一个明确的界定(TODO: )。
了解了 完全存储定序(TSO: Total Store Order)模型，我们来分析 章节 3 中例子 a,b 最终值 得一种可能的情形：

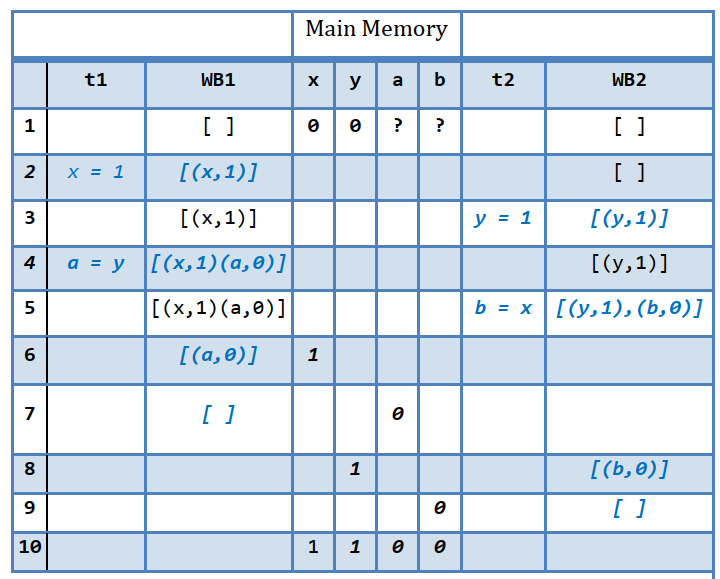
其中：

. 左边第1列表示指令执行顺序序列
. t1, t2 列分别表示绑定在 CPU 1,2 中执行的线程
. WB1 为 CPU 1 的 store buffer ，WB2 为 CPU 2 的 store bufferWBx 列 中的形如 [(x,1)] 表示 store buffer 队列中，缓存的变量 (x的地址，x的值1) 的二元组
. Main Memory 复合列表示各变量(x,y,a,b)在内存中的值

我们看到，在执行步骤 6 中，t1 (CPU 1) 将 store buffer 中的 (x,1) 出队，即将 x 的值1写入内存(Main Memory)，但很可惜，执行步骤 5 中， t2 (CPU 2) 从内存读取的 x 值是 0 (这时候 CPU 的 store buffe 缓存的值1 不能被 CPU 0 看到)，导致了 b 读取的 x 值为 0；类似的，a 读到的 y 的值也为 0 。但无论如何，上面分析的值只是 TSO 模型下，a, b 值的其中一种可能性。由于 CPU store buffer 中数据出列时间的不确定性，所以 a, b 最终值，从理论上分析，可能组合包括 (a=0,b=0), (a=1,b=0), (a=0,b=1), (a=1,b=1) 这4种可能性。
对 TSO 模型的介绍，暂时到此为止。如果想了解更多关于 TSO 模型的细节，可参考文章 《Taming TSO Memory Consistency with Models》 。

4.3 部分存储定序(PSO: Part Store Order)模型

章节 3 中提到的4种存储操作，允许 store-load，store-store 的存储操作乱序，其它操作保序。在 完全存储定序(TSO: Total Store Order)模型 下，我们例子中进程 B 中 temp 变量的值最后可能为 0 或 1 。

4.4 宽松存储(RMO: Relax Memory Order)模型

章节 3 中提到的4种存储操作，允许所有4种操作乱序。在 完全存储定序(TSO: Total Store Order)模型 下，我们例子中进程 B 中 temp 变量的值最后可能为 0 或 1 。

5. 内存屏障(memory barrier)

为了解决内存操作乱序引入的问题，引入了 内存屏障 (memory barrier) 来解决这些问题。如 ARM 的 DMB, DSB, ISB 指令等，更多关于 内存屏障 (memory barrier) 的细节将不在此处展开，感兴趣的读者可查找相关资料。

6. 参考资料

《perfbook.2018.12.08a.pdf》
《Taming TSO Memory Consistency with Models》

https://zhuanlan.zhihu.com/p/422848235
https://blog.csdn.net/anyegongjuezjd/article/details/125954805