文章目录
- 一、前言
- 二、前期准备工作
- 1.导入数据
- 2.探究关系
- 三、多元线性回归
- 1.训练模型
- 2.计算得分
- 3.可视化预测结果
------【机器学习第1天:线性回归(代码篇)】------
------【机器学习第2天:线性回归(理论篇)】------
------【机器学习第3天:预测汽车的燃油效率】------
一、前言
今天之所以选择这个主题是因为无意间看到另外一个博主做了这方面的预测,上一篇文章不是刚讲到多元线性回归这个点嘛,然后今天本来打算就这个点进行延伸,写一点相关知识点,然后觉得这个案例挺合适的,就准备拿它来进行扩展了。
然而,今天一天都栽在这上面了。事情是这样的,我依照上一篇文章的步骤,依次导入数据、整理数据、探究各个因素之间的关系。在可视化这步时却发现发现影响混凝土抗压强度的八个因素与它本身并不构成线性关系(查阅相关资料后证明这些因素与混凝土抗压强度是存在线性关系的)。
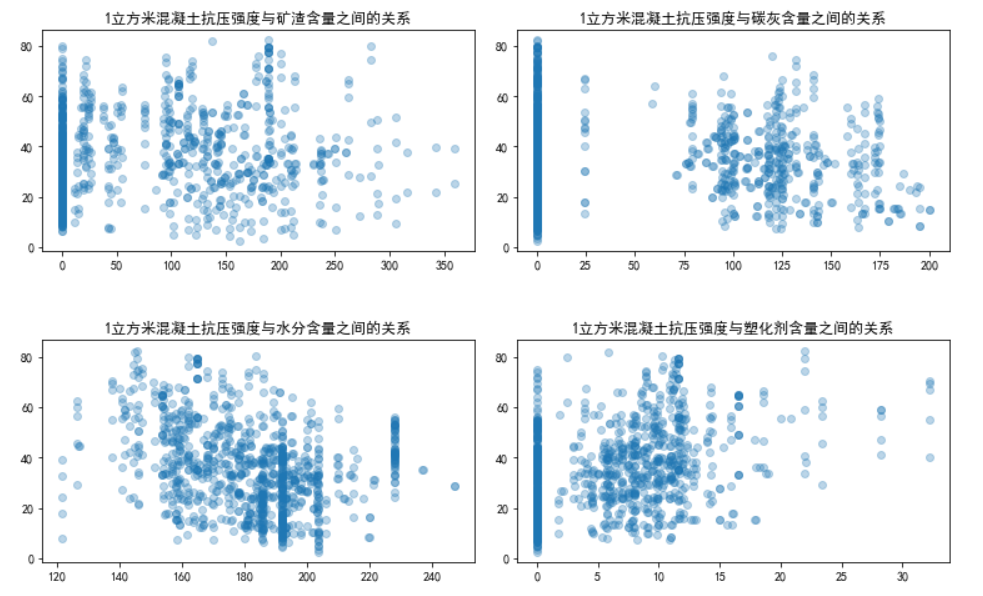
然后,一整天都在找原因,因为自己也正在学习ML的相关知识,所以就对自己产生了怀疑是不是自己的知识环节出现了问题呢,反复推理验证后,总结了如下几点:
- 1.线性回归模型的公式如下,如果某个值(
f)能通过线性回归模型来预测,那么它必然和它的影响因素成线性关系。
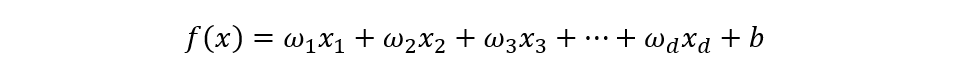
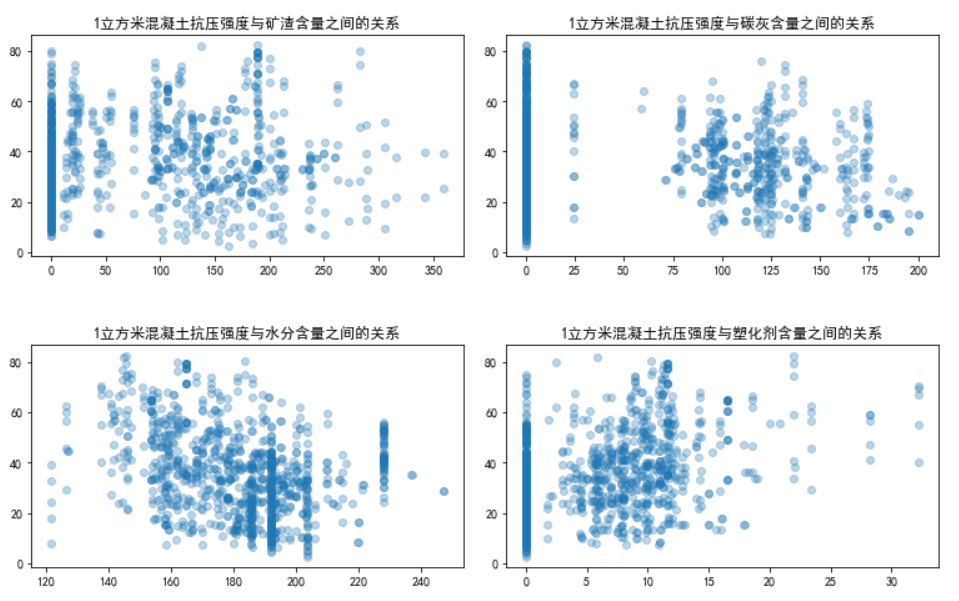
- 2.在线性关系探究的过程中若显示为散点形式或其他其他非线性形式,可能是由于该值与多个因素有关联加上数据量较少,扰乱了我们的视线。下图可以明显看出1立方米混凝土抗压强度在185、195、205、230处是受到除水分之外的其他因素的干扰,加上我这次数据量也仅1030条,让原本应该为线状散点图呈现了下面的样子
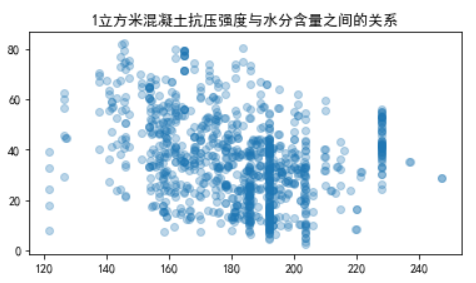
- 3.在关系探索中,如果可以尽量保持单一变量,比如上面我就应该保持除水分外其它因素(矿渣、煤灰等等)的不变。
心酸的一天,下面来看看我今天的代码吧
二、前期准备工作
1.导入数据
import pandas as pd
import matplotlib.pyplot as plt
"""
Cement: 水泥 (单位:千克)
Blast Furnace Slag: 矿渣 (单位:千克)
Fly Ash: 煤灰 (单位:千克)
Water: 水 (单位:千克)
Superplasticizer: 塑化剂(单位:千克)
Coarse Aggregate: 粗颗粒(单位:千克)
Fine Aggregate: 细颗料(单位:千克)
Age: 天数 (已经使用的天数)
Concrete compressive strength:1立方米混凝土抗压强度
大家拿到数据后注意观察数据头
"""
dataframe = pd.read_excel('../data/Concrete_Data.xls')
dataframe.head(5)

2.探究关系
import numpy as np#设置中文显示
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']fig = plt.figure(figsize = (13,17))
#调整子图间距
plt.subplots_adjust(wspace =0.1, hspace =0.4)
ax1 = fig.add_subplot(421)
ax2 = fig.add_subplot(422)
ax3 = fig.add_subplot(423)
ax4 = fig.add_subplot(424)
ax5 = fig.add_subplot(425)
ax6 = fig.add_subplot(426)
ax7 = fig.add_subplot(427)
ax8 = fig.add_subplot(428)
ax1.scatter(dataframe['Blast Furnace Slag'], dataframe['Concrete compressive strength'], alpha=0.3)
ax1.set_title('1立方米混凝土抗压强度与矿渣含量之间的关系')
ax2.scatter(dataframe['Fly Ash'], dataframe['Concrete compressive strength'], alpha=0.3)
ax2.set_title('1立方米混凝土抗压强度与碳灰含量之间的关系')
ax3.scatter(dataframe['Water'], dataframe['Concrete compressive strength'], alpha=0.3)
ax3.set_title('1立方米混凝土抗压强度与水分含量之间的关系')
ax4.scatter(dataframe['Superplasticizer'], dataframe['Concrete compressive strength'], alpha=0.3)
ax4.set_title('1立方米混凝土抗压强度与塑化剂含量之间的关系')
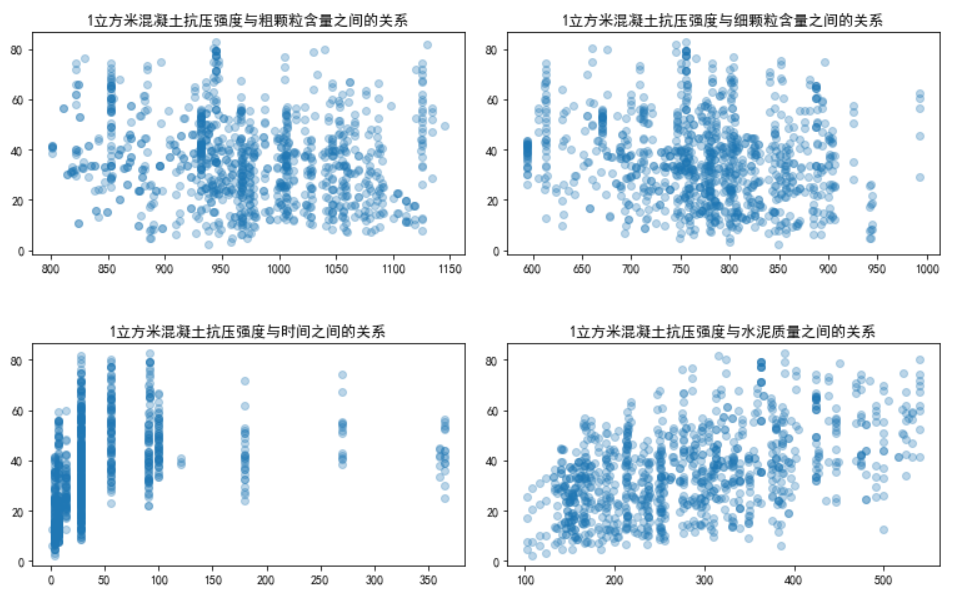
ax5.scatter(dataframe["Coarse Aggregate"], cars['Concrete compressive strength'], alpha=0.3)
ax5.set_title('1立方米混凝土抗压强度与粗颗粒含量之间的关系')
ax6.scatter(dataframe["Fine Aggregate"], cars['Concrete compressive strength'], alpha=0.3)
ax6.set_title('1立方米混凝土抗压强度与细颗粒含量之间的关系')
ax7.scatter(dataframe["Age"], cars['Concrete compressive strength'], alpha=0.3)
ax7.set_title('1立方米混凝土抗压强度与时间之间的关系')
ax8.scatter(dataframe["Cement"], cars['Concrete compressive strength'], alpha=0.3)
ax8.set_title('1立方米混凝土抗压强度与水泥质量之间的关系')
三、多元线性回归
1.训练模型
from sklearn.linear_model import LinearRegression#初始化模型
mul_LR_model = LinearRegression()#拟合模型
mul_LR_model.fit(dataframe[['Cement','Blast Furnace Slag','Fly Ash','Water','Superplasticizer','Coarse Aggregate','Fine Aggregate','Age']], dataframe['Concrete compressive strength'])
#预测
dataframe['预测值'] = mul_LR_model.predict(dataframe[['Cement','Blast Furnace Slag','Fly Ash','Water','Superplasticizer','Coarse Aggregate','Fine Aggregate','Age']])
#显示
dataframe.head(5)

2.计算得分
mul_score = mul_LR_model.score(dataframe[['Cement','Blast Furnace Slag','Fly Ash','Water','Superplasticizer','Coarse Aggregate','Fine Aggregate','Age']], dataframe['Concrete compressive strength'])
mul_score
"""
得分为:0.6154647342687214
"""
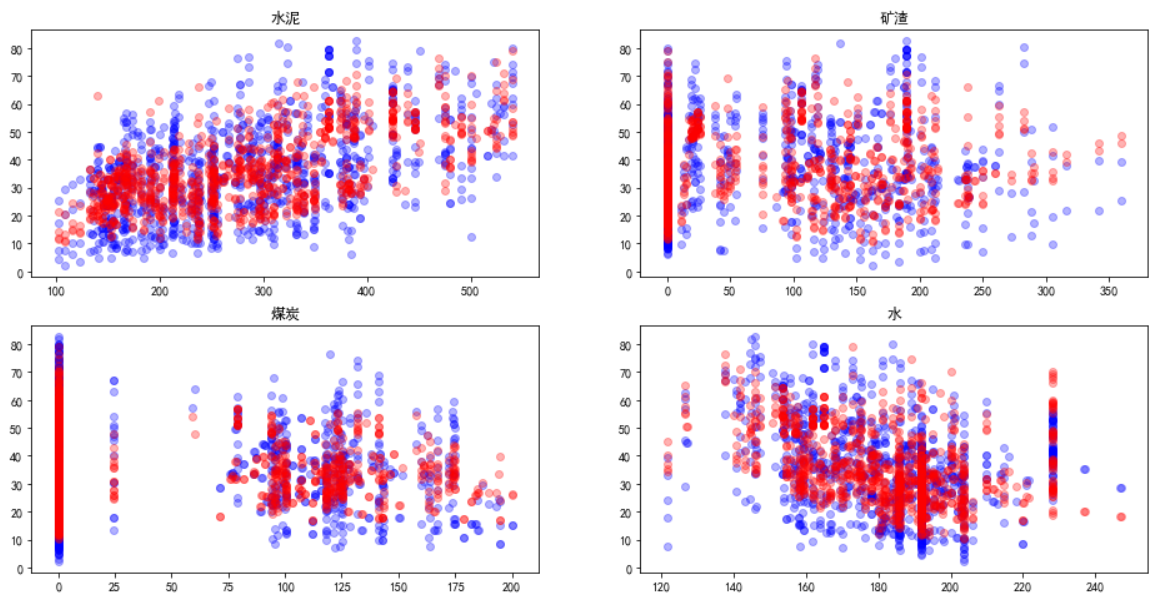
3.可视化预测结果
fig = plt.figure(figsize = (16,8))
ax1 = fig.add_subplot(2,2,1)
ax2 = fig.add_subplot(2,2,2)
ax3 = fig.add_subplot(2,2,3)
ax4 = fig.add_subplot(2,2,4)
ax1.scatter(dataframe['Cement'], dataframe['Concrete compressive strength'], c='blue', alpha=0.3)
ax1.scatter(dataframe['Cement'], dataframe['预测值'], c='red', alpha=0.3)
ax1.set_title('水泥')
ax2.scatter(dataframe["Blast Furnace Slag"], dataframe['Concrete compressive strength'], c='blue', alpha=0.3)
ax2.scatter(dataframe["Blast Furnace Slag"], dataframe['预测值'], c='red', alpha=0.3)
ax2.set_title('矿渣')
ax3.scatter(dataframe['Fly Ash'], dataframe['Concrete compressive strength'], c='blue', alpha=0.3)
ax3.scatter(dataframe['Fly Ash'], dataframe['预测值'], c='red', alpha=0.3)
ax3.set_title('煤炭')
ax4.scatter(dataframe['Water'], dataframe['Concrete compressive strength'], c='blue', alpha=0.3)
ax4.scatter(dataframe['Water'], dataframe['预测值'], c='red', alpha=0.3)
ax4.set_title('水')
plt.show()
------【机器学习第1天:线性回归(代码篇)】------
------【机器学习第2天:线性回归(理论篇)】------
------【机器学习第3天:预测汽车的燃油效率】------