jmeter如何测试一个get请求

news/2025/2/21 0:05:50/

目录

  • 1.配置测试计划
    • 1.1.创建线程组
    • 1.2.创建GET的HTTP请求取样器（模拟GET请求）
    • 1.3.添加查看结果树和聚合报告
  • 2.执行压测并查看结果
    • 2.1.验证接口
    • 2.2.执行压力测试

使用jmeter测试一个http的get请求示例.

1.配置测试计划

1.1.创建线程组

打开jmeter - 测试计划右键 - 添加 - 线程（用户） - 线程组
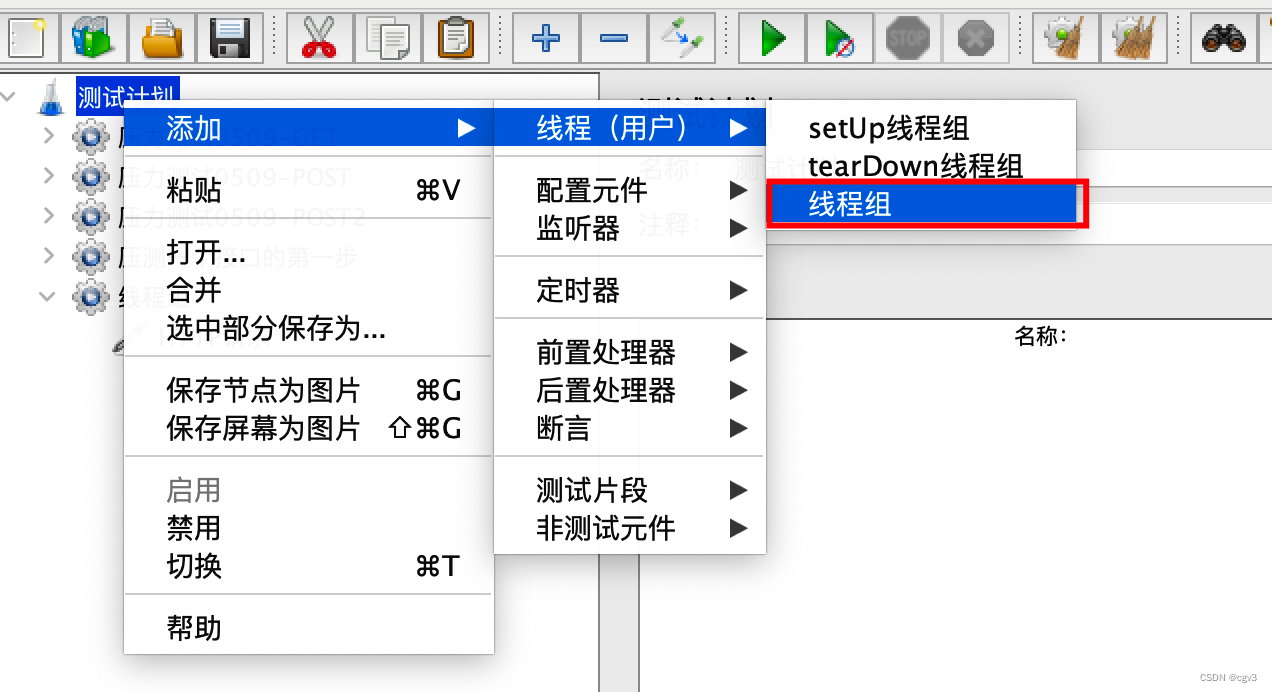
在这里插入图片描述

配置线程组的基本参数（主要3个）

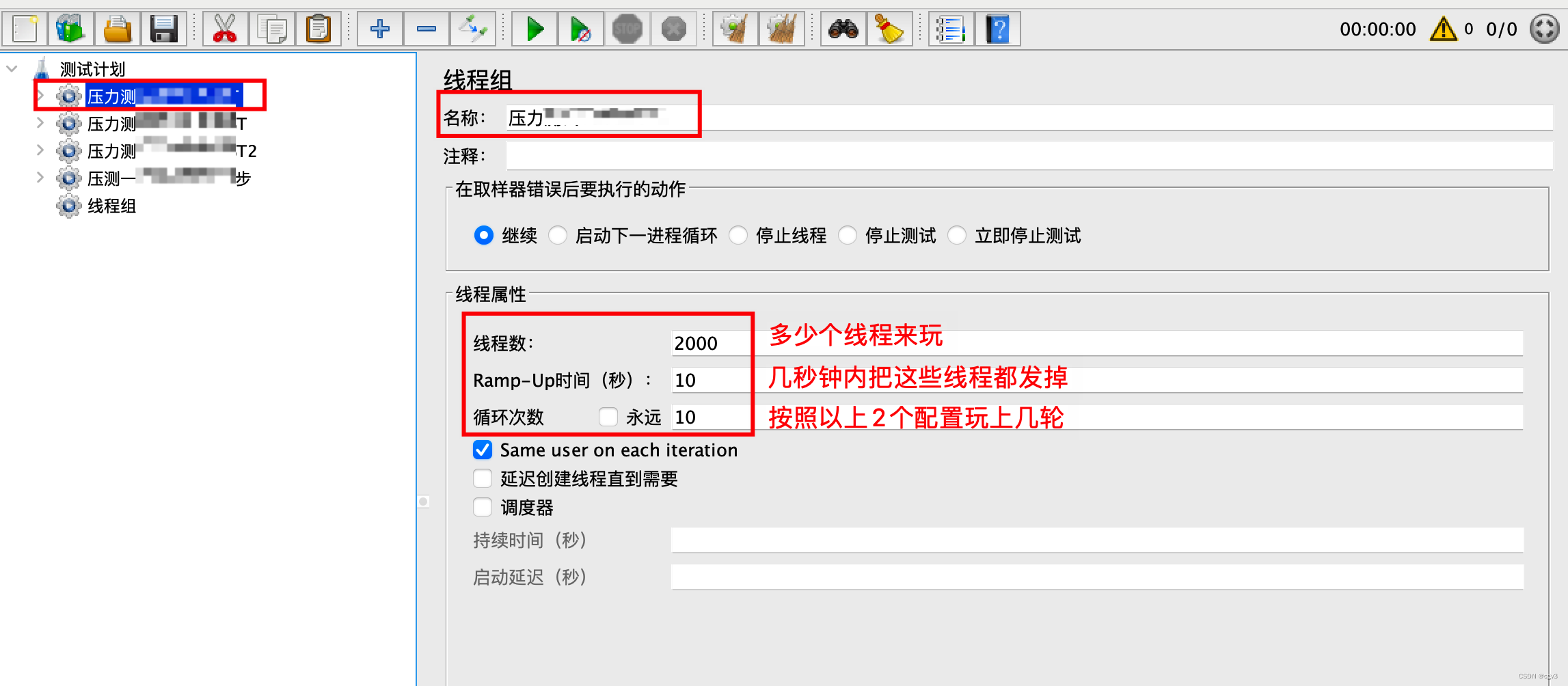
在这里插入图片描述

1.2.创建GET的HTTP请求取样器（模拟GET请求）

线程组右键 - 添加 - 取样器 - HTTP请求
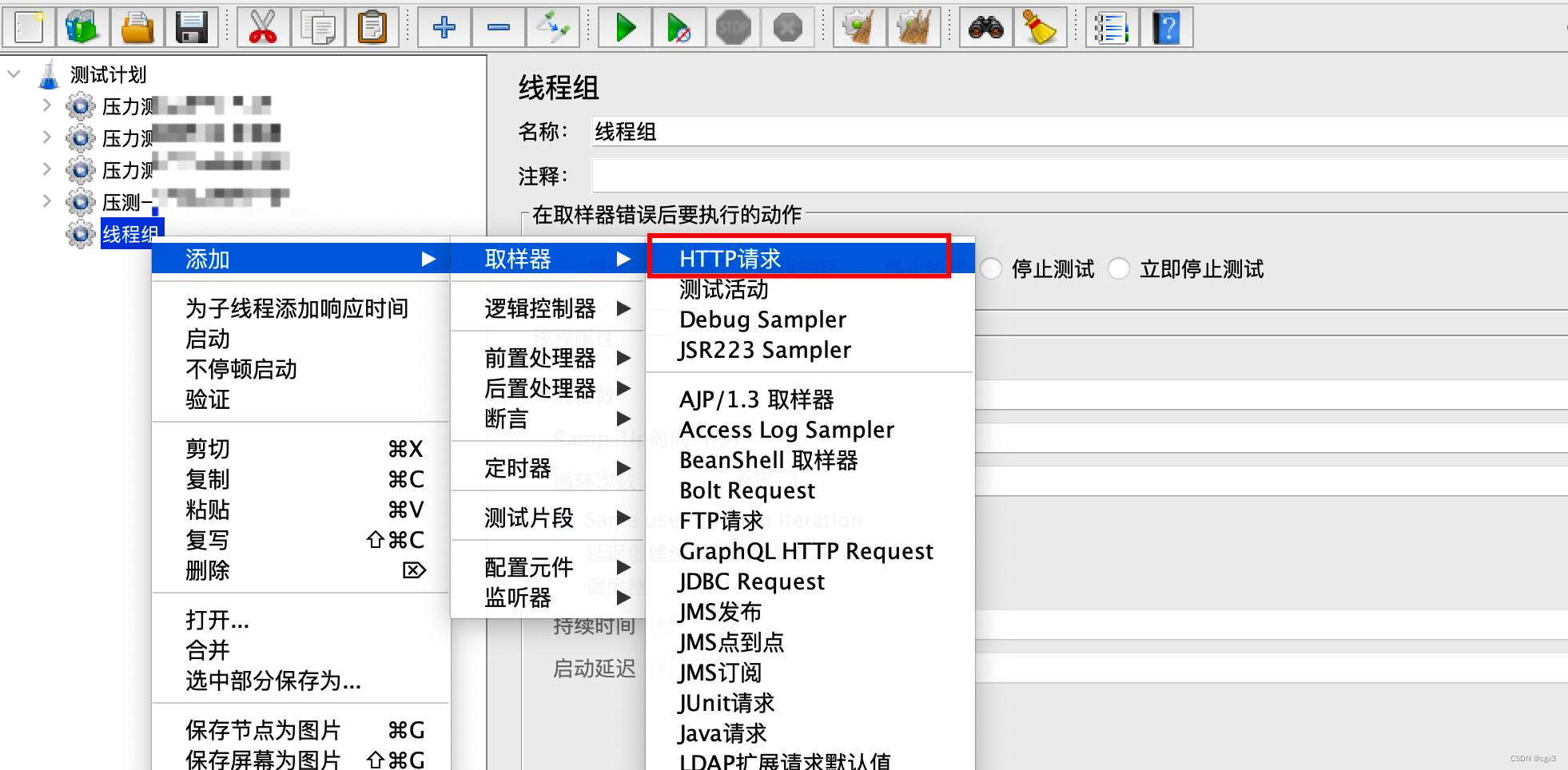
在这里插入图片描述

补充GET请求相关的参数

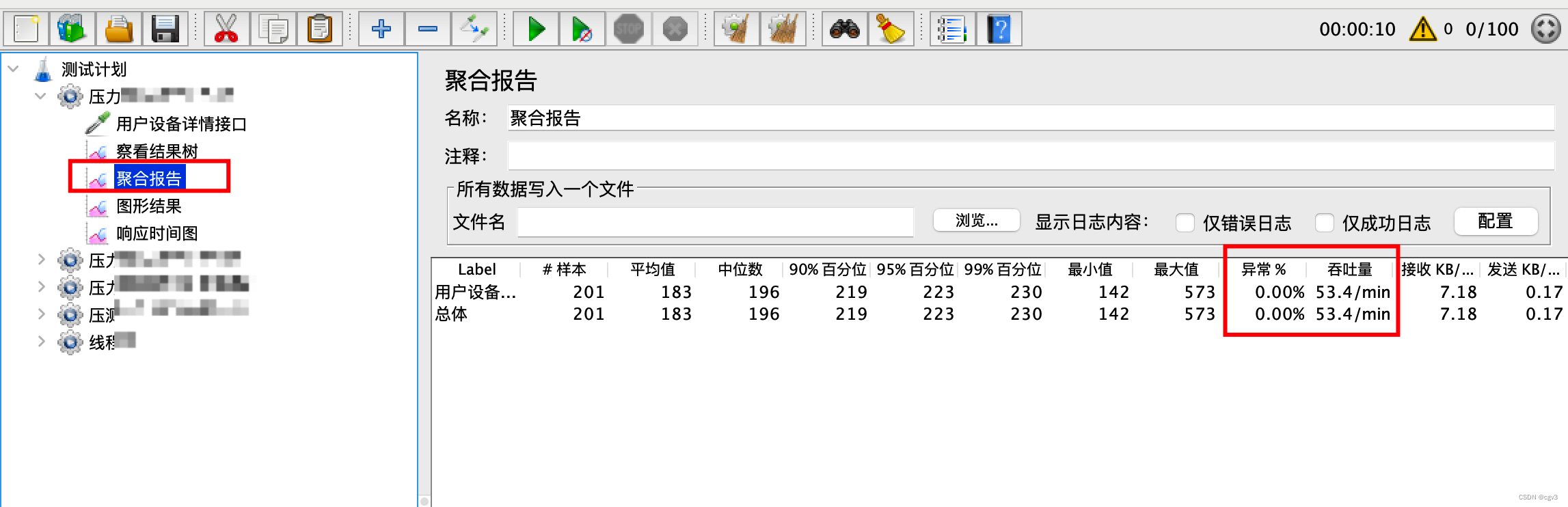
在这里插入图片描述

1.3.添加查看结果树和聚合报告

线程组右键 - 添加 - 监听器 - 查看结果树/聚合报告

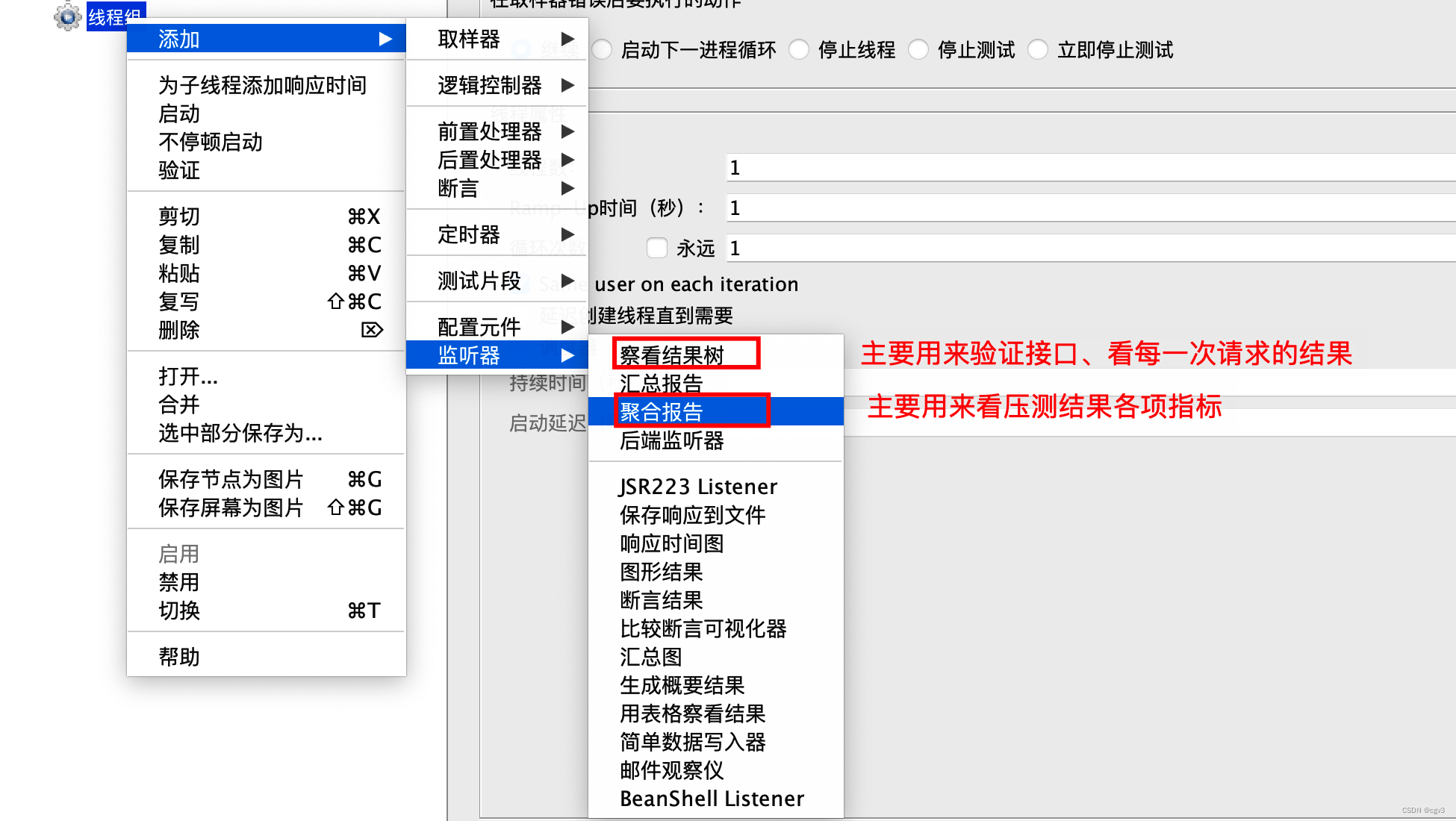
在这里插入图片描述

添加好一个测试模型后如下图所示：

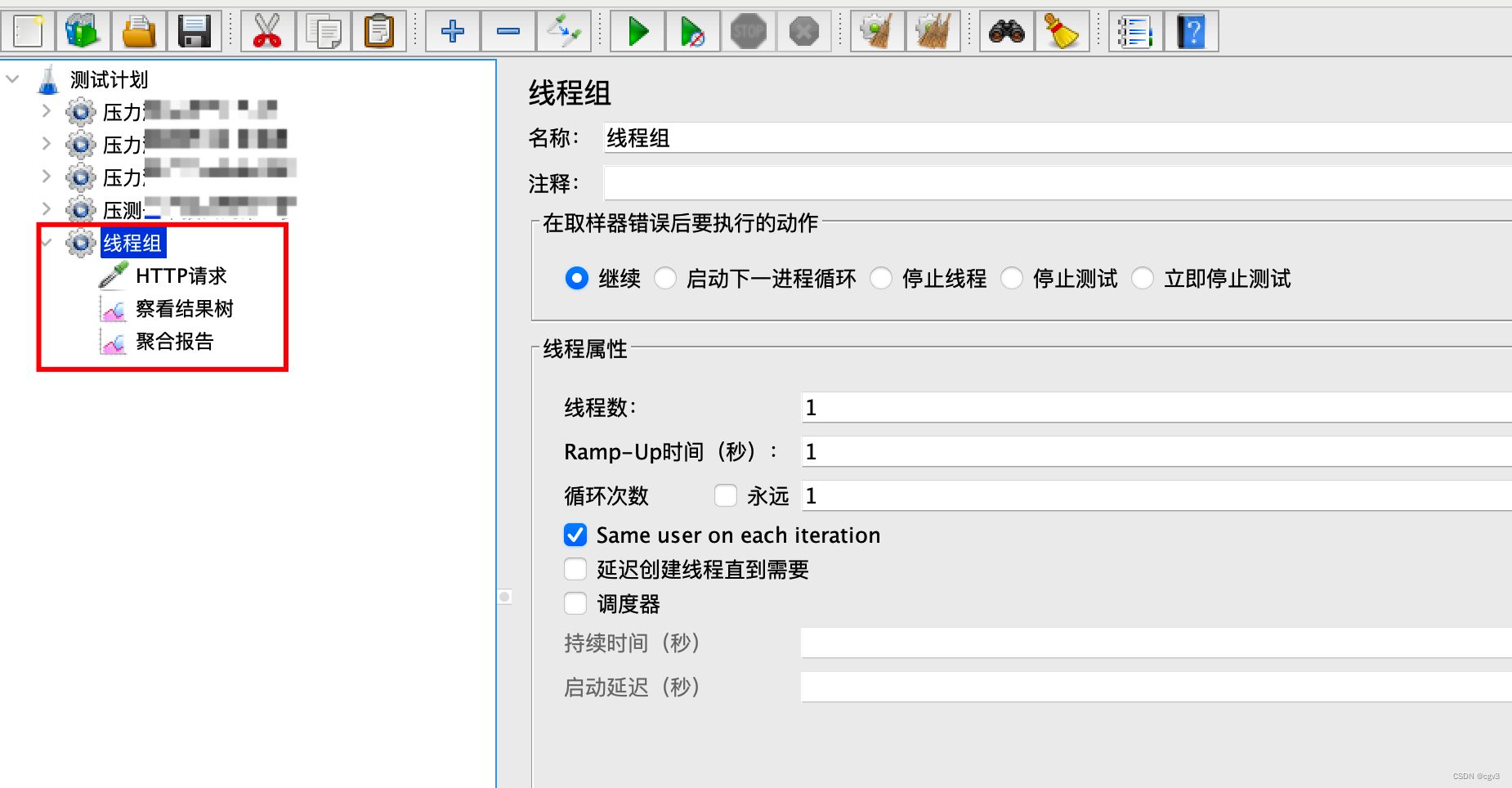
在这里插入图片描述

2.执行压测并查看结果

2.1.验证接口

只有验证通过了才能进行压力测试，其实就是发送一次请求试试，结果在查看结果树菜单下查看

线程组右键 - 验证
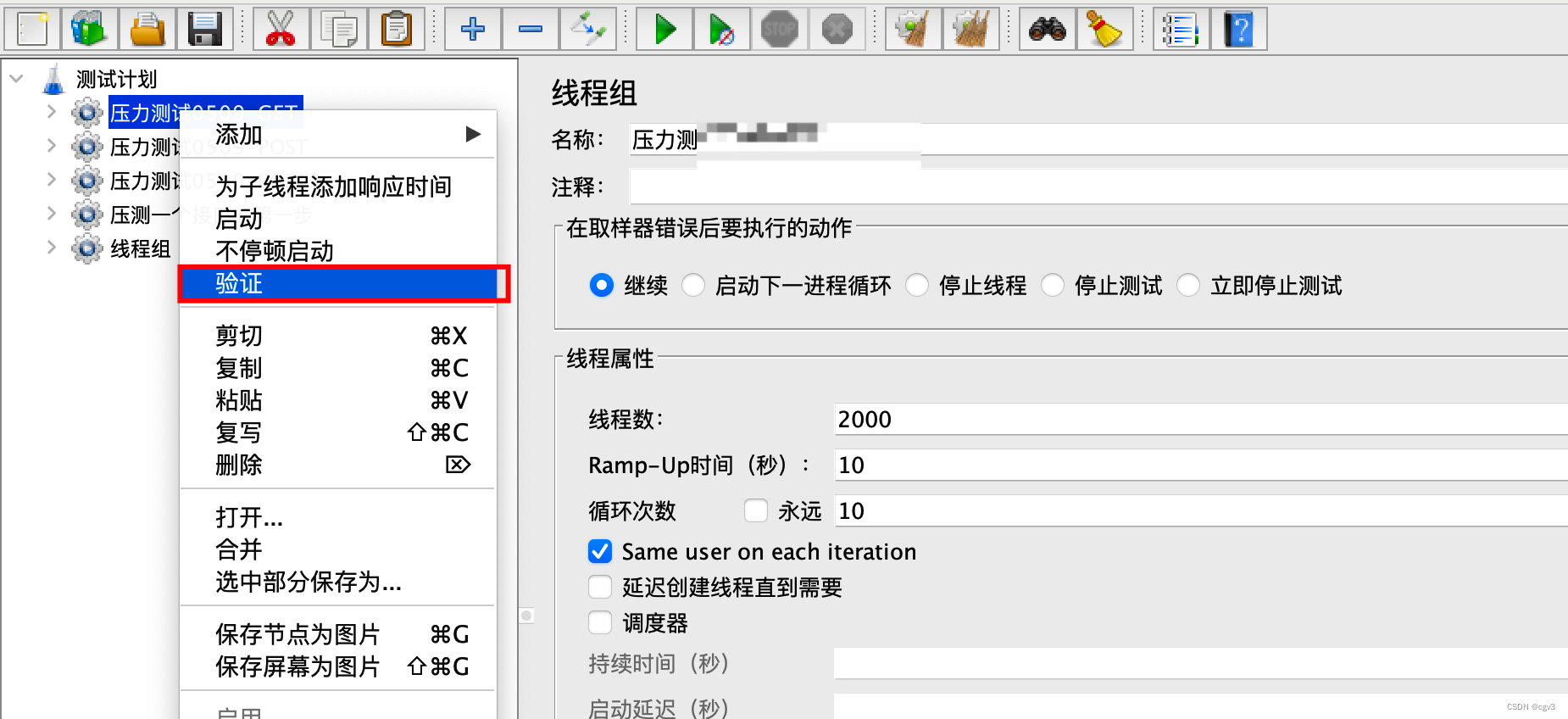
在这里插入图片描述

查看验证结果

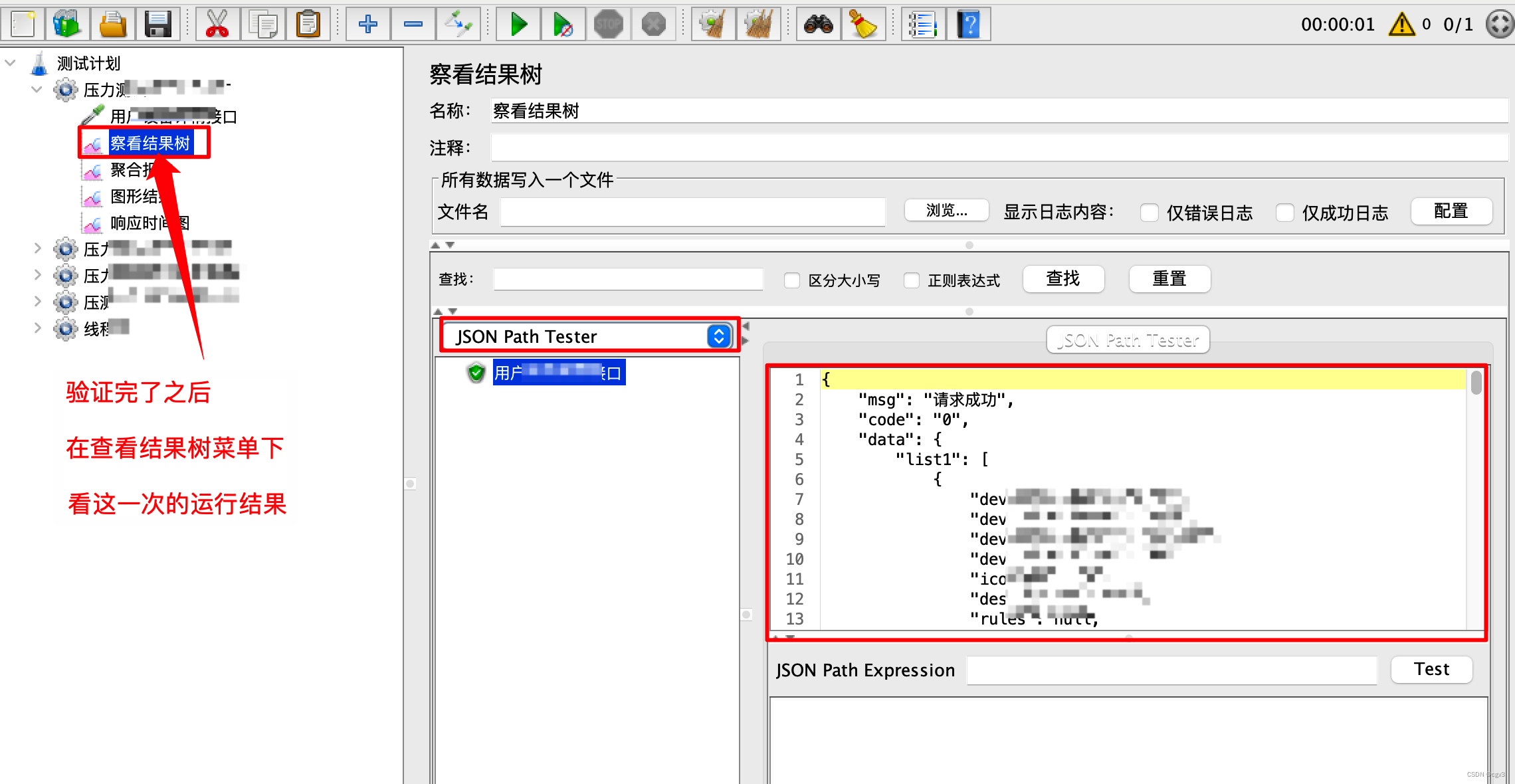
在这里插入图片描述

2.2.执行压力测试

线程组右键 - 启动

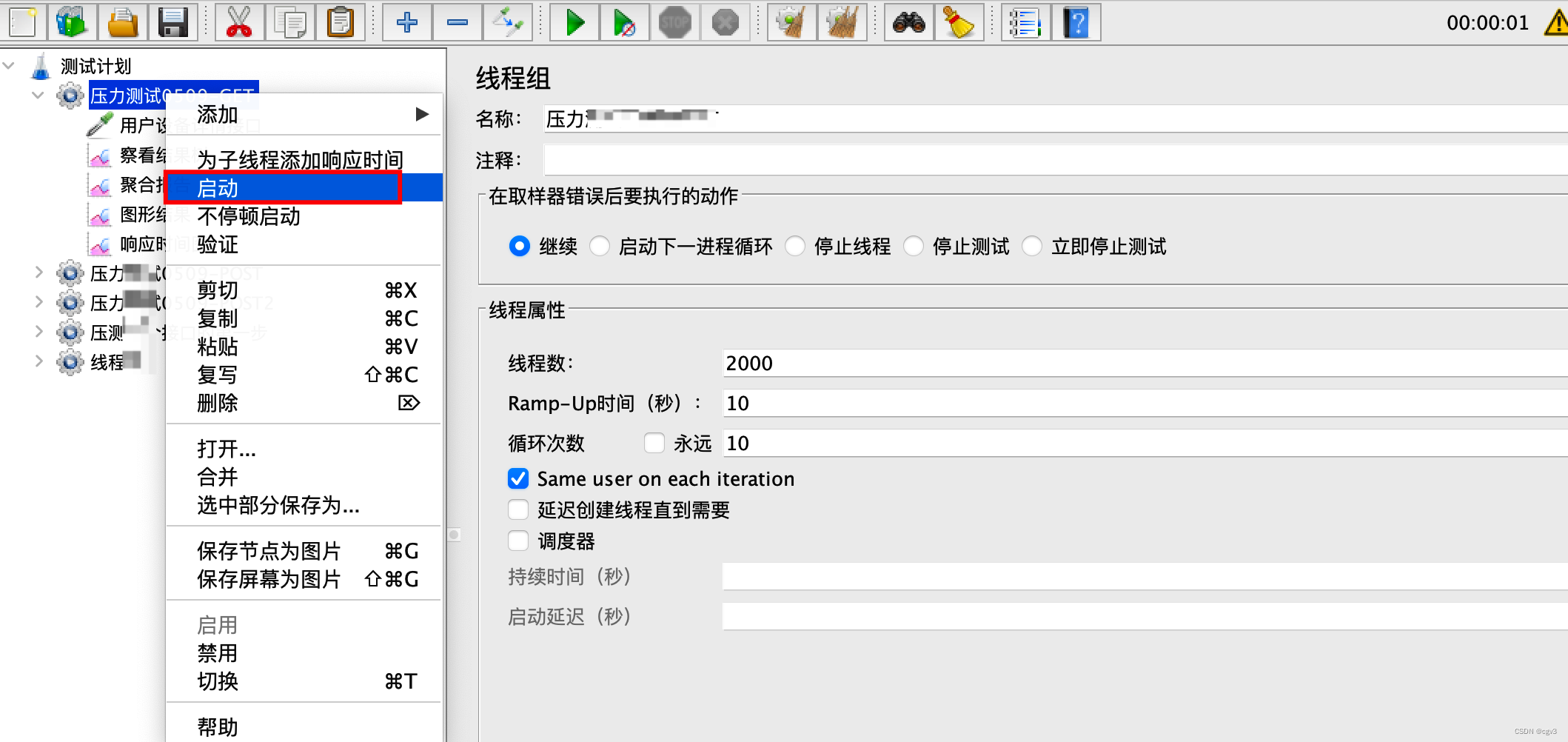
在这里插入图片描述

等着跑完了就可以查看聚合报告

在这里插入图片描述


http://www.ppmy.cn/news/66891.html

相关文章

前端CSS学习（一）

前端CSS学习（一）

1、基础认知 CSS概述&#xff1a;CSS:层叠样式表(Cascading style sheets)CSS作用是给页面中的HTML标签设置样式&#xff0c;起到美化修饰网页的作用CSS语法规则&#xff1a;CsS写在style标签中&#xff0c;style标签一般写在head标签里面&#xff0c; title 标签下面<!DOC…
阅读更多...
向量时钟算法

向量时钟算法

向量时钟不仅同步本进程的时钟值&#xff0c;而且还同步已知的其他进程时钟值 分布式系统中每个进程Pi保存一个本地逻辑时钟向量值VCi&#xff0c;VCi(j)代表进程Pi知道的进程Pj的本地逻辑时钟值 初始化VCi向量为[0,…]进程Pi每发生一次事件&#xff0c;VCi[i]加一进程Pi给进…
阅读更多...
多媒体通信有些SCI期刊推荐？ - 易智编译EaseEditing

多媒体通信有些SCI期刊推荐？ - 易智编译EaseEditing

以下是一些多媒体通信领域的SCI期刊推荐&#xff1a; IEEE Transactions on Multimedia&#xff1a; 这是IEEE计算机学会旗下的一个期刊&#xff0c;涵盖了多媒体信号的处理、编码、压缩、传输和交互等方面的研究。 ACM Transactions on Multimedia Computing, Communication…
阅读更多...
五步看平台，选好安全的MT4交易外汇平台

五步看平台，选好安全的MT4交易外汇平台

在选择MT4外汇交易平台时&#xff0c;如何避免不正规的平台?以下是5招教你远离不正规MT4交易外汇平台。 1. 查看平台是否取得合法许可证 首要考虑的是该平台是否取得了合法的许可证。许可证是证明一个交易平台合法的最重要证据&#xff0c;因此务必在选择时核查该平台的许可证…
阅读更多...
面试必问 - AES 加密 和 RSA 加密是什么？它们有什么区别

面试必问 - AES 加密 和 RSA 加密是什么？它们有什么区别

1、什么是 AES 加密 和 RSA 加密&#xff1f; AES&#xff08;Advanced Encryption Standard&#xff0c;高级加密标准&#xff09; AES 是一种对称加密算法&#xff0c;即加密和解密使用相同的密钥。AES 的密钥长度可以选择 128 位、192 位或 256 位。AES 的加密过程包括多轮…
阅读更多...
OLS样本估计量抽样分布模拟

OLS样本估计量抽样分布模拟

OLS样本估计量抽样分布模拟 文章目录 OLS样本估计量抽样分布模拟1 OLS估计量分布2 R语言实现 1 OLS估计量分布 对于线性回归方程 Y β 0 β 1 X ε Y \beta_0\beta_1 X \varepsilon Yβ0​β1​Xε 利用普通最小二乘法(OLS&#xff09;估计上述方程参数使的假定(之一)是…
阅读更多...
STM32-江科大

STM32-江科大

新建工程 引入启动文件 Start中是启动文件&#xff0c;是STM32中最基本的文件&#xff0c;不需要修改&#xff0c;添加即可。 启动文件包含很多类型&#xff0c;要根据芯片型号来进行选择&#xff1a; 如果是选择超值系列&#xff0c;那就使用带 VL 的启动文件&#xff0c;…
阅读更多...
四元数插值Eigen源码解析

四元数插值Eigen源码解析

四元数插值公式 Slerp ⁡ ( q 0 , q 1 ; t ) sin ⁡ [ ( 1 − t ) Ω ] sin ⁡ Ω q 0 sin ⁡ [ t Ω ] sin ⁡ Ω q 1 , 0 ≤ t ≤ 1 {\displaystyle \operatorname {Slerp} (q_{0},q_{1};t){\frac {\sin {[(1-t)\Omega }]}{\sin \Omega }}q_{0}{\frac {\sin[t\Omega ]}{\s…
阅读更多...
最新文章

Copyright @ 2022~2023