此文是转载!略有改动!
原文:https://www.sohu.com/a/250248840_614593
我们在学校里都学习过棱柱和棱锥这些立体,其中就包括它们体积的计算公式,我们说一个棱锥的体积是同底等高的棱柱的体积的三分之一 。这当然是正确的,但是,包括您在内的我们,是不是在心里问过,为什么就是三分之一?怎么不是二分之一,也不是四分之一呢?或是其他的什么分之一?
我就反问过自己。虽然看到过做实验,比如用豆子或小米或水,但实验只能给出一个感性的印象,我们还需要理论证明。我怎么也看不出来这个三分之一是怎么得到的。后来也学习了圆锥的体积是同底等高圆柱体积的三分之一。反正这个三分之一也不难记,我们就记住它了。几十年过去了,我现在搞懂了,所以,我想在这里把这个三分之一是怎么得来的讲给您听,也许你知道,也许不知道,但相信这其中的奥妙仍然会很吸引人。请您继续往下看,不会让您失望的。
我们画一个三棱柱ABC-DEF,如下图所示。注意,不要求它是“直”的,即侧棱不一定与底面垂直。更不要求它是的“正”,即底面不一定是正三角形。这样的三棱柱,它的上、下底面是全等的三角形,并且经平移可以互相重叠;它的三个侧面都是平行四边形。
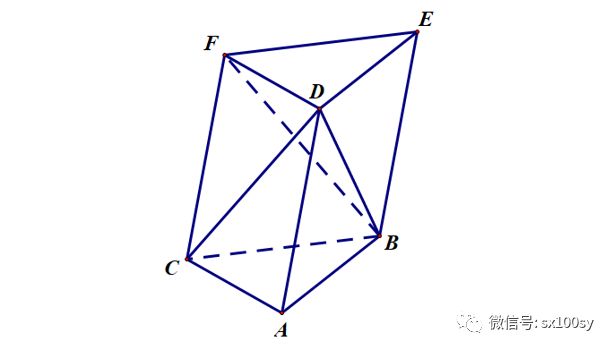
接下来,我们连接DB和DC。于是,D-ABC是一个与三棱柱同底等高的三棱锥。我们要证它的体积是三棱柱体积的三分之一。若可以得证,则三棱锥体积是同底等高三棱柱体积的三分之一这一结论就成立了。这个结论是通用的,即不管这个三棱锥是什么样子,公式都成立。这是因为我们总可以在先有一个三棱锥的情况下,构造出一个同底等高的三棱柱,让这个三棱柱的一条侧棱就是三棱锥的一条侧棱(比如上图中的AD)。
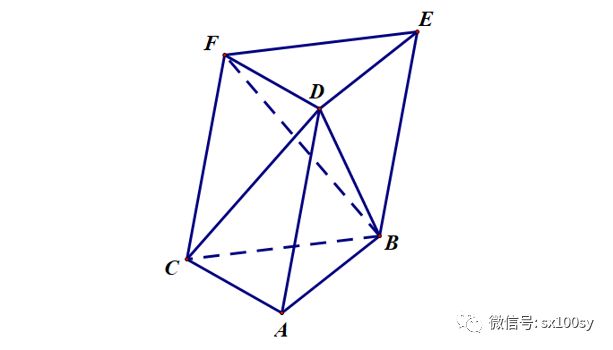
于是,三棱柱ABC-DEF就被分割成了两部分:三棱锥D-ABC和四棱锥D-CBEF(注意,我们在表示一个棱锥时,是把锥顶字母写在前面,后面画一短杠,再接着写表示底面的字母)。
接下来,我们连接BF,即四棱锥D-CBEF底面平行四边形CBEF的对角线。于是,四棱锥D-CBEF可以看成是由两个三棱锥构成的:D-CBF和D-BEF。因为它们有相同面积的底面CBF和BEF,并且等高,所以体积相等。下面只需证明这两个三棱锥之一与D-ABC体积相等。有两种方法来证明,都很简单。
方法一: 把三棱锥D-BEF写成B-DEF,就相当于我们以B为顶点以DEF为底面,于是,显然,三棱锥B-DEF与三棱锥D-ABC因等底等高而体积相等。
方法二:把三棱锥D-CBF写成B-CDF,而B-CDF与B-ACD(即D-ABC)等底等高,体积相等。最终,我们证明了这个三棱柱被分成的三个三棱锥的体积相等,而其中一个就是与三棱柱同底等高的三棱柱,所以,我们最终就证明了一个三棱锥的体积等于同底等高三棱柱的体积的三分之一。
最后需要说明,任意棱锥的体积等于同底等高的棱柱的体积的三分之一,是因为我们可以把棱锥分割成一个个的三棱锥。把它们加起来即可。