量子多体理论和量子场论之间有什么异同呢？

我粗略的看了文小刚老师的《量子多体理论》，发现基本上这里面的内容我曾经都在学量子场论的过程中计算过，除了最后的弦网凝聚以及量子霍尔效应中流体力学方法。

可以初步认为，量子多体理论可以看成欧几里德空间量子场论与格点量子场论的结合。前者是wickrotation后的量子场论，后者可以先考虑Z_2对称性，然后推广到更一般的Z_n对称性。

一般来说，量子多体理论指的是涉及粒子数量较大（凝聚态系统）、关注能量较低过程的量子场论，因为能量较低，没有高能意义下的粒子生灭。

谷歌人工智能写作项目：爱发猫

量子多体理论和量子场论之间有什么异同

量子多体纠缠比量子场更基本吗？

。

量子学领域是非常尖端的领域，除了世界上顶尖的几个国家之外，几乎没有更多的国家涉及到量子科学领域，我国在量子学领域就已经在世界上处于领先地位，那么有关量子学的一些科研创新，实际上在很多顶尖杂志上也出现过众多的讨论，其中就包括量子多体纠缠比量子场更基本吗？

其实有关于量子多体纠缠理论已经有一些经典著作，可以发现量子多体纠缠理论都是通过量子场理论通过不断计算得到，最后通过一些特殊的效应和流体力学的方法总结出了量子多体理论，但是有关于量子现象的理论经典物理学无法解释，所以只能通过一些模型的构建来更好地理解或推测量子多体纠缠，在很多经典量子学名著当中也展现了量子纠缠的特征，也就是说至少要需要两个量子粒子才可以发生量子纠缠，这也似乎表明，量子纠缠的相关非定域性可能是量子世界一个比量子干涉或者量子场更基本的性质。

量子纠缠进入了量子力学的核心，量子多体纠缠结果表明单个粒子量子效应可以成功在经典本体论模型中展现，但是访问有限，因此多粒子现象基本处于非定域性，所以量子多体纠缠可能是更符合量子力学以及量子领域的相关特性，甚至是组成量子场的基本单位，所以根据相关结论和推论量子多体纠缠在定义上面会比量子场更基本。

在日常利用量子进行通讯的时候，基本上也就是利用量子之间的纠缠效应，进行信息传递，逐渐形成的新的通讯方式，而且量子纠缠无法描述单个粒子的性质，只能描述整个系统的静止现象，这也间接性地说明了量子纠缠可能是量子场最基础的单位，因为量子场当中就含有很多量子单位，就需要每一个单个的量子进行相互活动产生量子纠缠力学现象，逐渐形成量子场。

有哪些适合学数学的学生看的关于量子力学和量子场论的书

一般当我们提到量子场论，我们是指相对论量子场论。

我第一次上量子场论课是一个核物理方面的教授，主要用的教材是Greiner的相对论量子力学+场量子化+量子电动力学Peskin的量子场论导论Greiner的书写得十分详细，我觉得这是一个优点也是一个缺点。

优点是，每次我看Peskin上含糊不清地时候，可以翻一下Greiner，他一般会有一些解释。

缺点是，我不认为如此详细的书籍适合自学，首先这本书写得不是很有吸引力，加上那么多细枝末节，所以在毅力和时间的斗争中，我相信很少有人能坚持到最后。

Greiner的书还有个特点是他的这一套书是一个完整的体系，显然，这是一个优点也是一个缺点。特别是当你看着书，老是会时不时地引用一下其他几本书的结论时。

Peskin的书我的感觉是这本书适合一个仔细研读过这本书，并对场论框架有自己理解的老师带领着学生学习，一般不适合自学。

Greiner和Peskin的书的体系有一个共同点，就是标量场、旋量场、矢量场一起量子化，这方便我们看到不同自旋的场的量子化的差异。但是背包上有太多行囊，就难以到达远方。

量子场论里面有很多必要的数学技巧和细节，比如旋量场的gamma矩阵，矢量场的规范处理等等，反而很容易让我们迷失在这些细节中，而一下子看不到场论整体的框架。

后来我又上了一次量子场论，是一个资深的粒子物理学教授开的。用的教材是Srednicki的量子场论。这位老师将量子场论课分为I和II，开了一学年的课。

其中第一学期，只讲了Srednicki这本书的spin-0部分，也就是只讲标量场。第二学期，讲了Srednicki这本书的spin-1/2和spin-1两部分，也就是旋量场和矢量场。

这本书的特点很明显，Srednicki更加注重场论框架的建立。标量场没有很丰富的内禀结构(自旋、规范)，所以通过标量场的讲解，我们可以把注意力完全关注在场论的结构上。

场的量子化，渐近展开，费曼图，重整化(群)，对称性自发破缺。

这些在标量场的框架下就可以清晰地展示出来，接下去讲到旋量场和矢量场，采用的仍是相同的框架，只是慢慢地把内禀结构加上去，比如处理自旋，我们引入洛伦兹群和gamma矩阵，处理规范，我们引入群表示论等等。

当然我觉得这样一种讲法和Peskin的那种讲法互为补充，可以让我们关注到场论的不同结构。毕竟场论结构不能简单粗暴的根据自旋来区分。

首先我觉得Srednicki这本书是适合自学的，因为你如果能在激情磨灭前学完partI，我觉得已经足够让你领略到场论的结构了，相比于Peskin里面需要自己脑补很多细节，Srednicki简直就是手把手告诉你细节。

但是说实话，这本书给我的感觉就像当初学量子力学看Griffiths，读起来感觉很合理，但实际上有点避重就轻，很多细节根本不像书上那样能够一笔带过。

这时候就不得不提到装逼利器，Weinberg的三卷本量子场论。

我猜测有些场论狂人是可以直接通过学习这三本而学好量子场论的，比如xuc.k或qix.l反正每次Srednicki里面闪烁其词时，我总能在Weinberg里面找到合理的论述，不过对于我这样一个做凝聚态理论的人而言，啃完这三本实在是有点星辰大海的感觉。

另外A.Zee的书我没看过，暂时不做评论。

一般场论有两种formalism分别是canonicalformalism和pathintegralformalism早期场论的建立，一般都是基于canonicalformalism这个在凝聚态场论里很容易理解，因为二次量子化是表述多粒子体系一个很自然的表象，场论的很多结构直接内蕴在算符的对易关系中基于canonicalformalism的多体理论有三本书第一本是苏联朗道学派的统计物理学中的量子场论方法，一般称为AGD这本书的经典性随着时间愈发明显，特别是随着非常规超导的研究，虽然不能用基于电声耦合来解释配对机制，但是超导copper对的场论描述仍旧可以放入原来的框架。

我本科毕业论文就是基于这本书以及60年代AGD的论文来处理非常规超导中的杂质效应。第二本是美国的Fetter的多粒子物理的量子理论。AGD从某种程度上属于惜墨如金，短小精悍，需要自己脑补很多计算细节。

而Fetter这本书不同，光是二次量子化，他就整整讲了一章。如果想对二次量子化有个更深入的了解，又不想看半个世纪之前那些专著，我个人觉得这一章就是那个年代二次量子化的精华了。

这本书是和一个核物理教授一起写的，我对核物理不了解，不过当原子核里面强子比较多，并且速度不那么快时，这也就变成一个非相对论多体问题，和一般凝聚态研究的固体可以放入同一个框架。

所以我觉得这本书是非常适合自学的，只是需要足够的毅力，毕竟它不像AGD那么薄。

第三本是Mahan的多粒子物理这本书是一本很明显的实用主义特色的书籍，他告诉你怎么用二次量子化，怎么用wick定理，告诉你费曼规则，但是他说不清为什么。

如果你是那种喜欢刨根问底的人，那么这本书会让人非常难受。但是如果你想以短时间学会怎么做，那么这本书很适合你。

相比于前两本书，这本书唯一的优点是出版时间比较晚，所以包含了一些相对新近的内容，比如一些强关联模型，比如量子霍尔效应。

我个人对这本书的看法就像对曾谨言的量子力学，没事不要花时间去看它，有什么问题了可以翻一翻，没准有什么帮助，毕竟只是一本工具书，没太多物理。

如果只是处理一些微扰问题，canonicalformalism和pathintegralformalism其实都够用，无非就是你熟悉哪一套，是西方那一套还是蛤蛤。

但是随着量子霍尔效应和高温超导的出现，凝聚态开始关注强关联问题，传统的微扰论在这里失效了。

一些新的方法浮现出来，如stationaryphaseapproximation，renormalizationgroup等，这些方法在pathintegralformalism可以很清晰的展现出来，相应的，很多专著也开始用pathintegralformalism来重新表述凝聚态场论。

我这边讲一点我看过的几本书。第一本，文小刚的量子多体理论。类似Srednicki根据自旋来分类场，文小刚的书前几章是根据波色子和费米子来分类场。

从数学细节上来说，波色子可以用复数来描述，费米子要用Grassmann数来描述。不过任何分类有得必有失，很多很重要的结构，如格林函数、重整化群在这里变成了一个计算细节。

不过文小刚这本书很优秀的是单独一章讲解格点规范理论，这在早先的教材里是完全没有的，但却是理解强关联问题一个很重要的部分。

不过说实话，文小刚的书称之为有点妖，或者说思想诡谲，而且夹带了很多私货，初学者切莫陷得太深。但是如果你有一定的凝聚态场论基础，这本书肯定能给你很多启发。我想清华的人这本书一般玩的很溜。

第二本，Nagaosa的两本凝聚态/强关联中的量子场论或许是因为Nagaosa是从本科生都熟悉的量子力学开始讲起，很多人觉得这本书似乎不难，但是前提是你没有走到第三章及之后。

在我看来，Nagaosa这本书绝对是把凝聚态场论中最基本而又重要的概念用最合适的例子以最少的笔墨描述出来。如果第一次学凝聚态场论用这本书，从第三章开始就会步履维艰。

既然Nagaosa惜墨如金，标量场、矢量场、规范场肯定是一起量子化的，而且很多细节显然不够充分，所以我觉得这本书更适合学过一遍凝聚态场论后，再系统地回顾一下。

第三本，Tai-KaiNg的IntroductiontoClassicalandQuantumFieldTheory这本书在序言里就表明，这本书就是为了给上面两本书入门而写的我个人觉得这本书确实很适合入门，不过由于作者是我老板的博后老板，所以也算是广告吧第四本，Altland&Simons的CondensedMatterFieldTheory这本书很适合自学，因为考虑到这本书的编排，我也很难想象有人会拿它当教材上课，不过自学需要有正确的打开方式说实话，这本书每一章我觉得讲得都逻辑不畅，乱七八糟，但是当它把这些内容按照一定顺序组织起来，忽然那个感觉就来了，或许这也是凝聚态的魅力这本书也算不上事无巨细，所以很多计算细节还得自己脑补，但是这本书的特点就是你花了多少时间，你就能从这本书收获多少这本书分了两个章节来讲重整化群和拓扑，我觉得是这本书的精华，千万不能错过虽然重整化还没Shankar讲得好，拓扑肯定也没Nakahara讲得细这本书第二版加入了非平衡态场论的部分，我暂时还没做过相关的课题，暂时不做评论唯一的缺憾是这本书没有格点规范场论这样一章，有可能和作者的研究领域有关第五本，Negele&Orland的QuantumManyParticleSystems作为ABC这一系列书的一员，这本书的地位我也无需多说我相信读完这本书需要极大的毅力，它那密密麻麻的小字，可能有时候你花了一小时，才发现读懂了一张纸。

但是这本书细节肯定是完备的，框架也是清晰的，所以剩下的都是读者的问题了这本书还有个特点，它很多精华居然都是以习题的形式出现，所以如果你没做过习题，就跟没看这本书差不多唯一的遗憾时，作为一本类似AGD这样经典的书，这本书没有很多新近的内容，比如量子霍尔效应之类，这一点可以借由Altland&Simons的书来补充，从与时俱进这一点，Altland&Simons做得很优秀。

最后再提一本小黄书，Auerbach的相互作用电子和量子磁性这本书的附录是精简版的pathintegralformalism的凝聚态场论这本书主要以量子海森堡模型为例展示凝聚态场论的框架如果说量子力学背后的数学是线性代数的话，那么量子场论这门课本质上也是一种代数的学习代数，除了告诉我们一套计算规则之外，更重要的是告诉我们对象的结构/框架量子场论背后的代数结构十分丰富也十分复杂，我们可能只是窥到了它的冰山一角PS：最后介绍凝聚态场论几本书时有点匆匆忙忙一笔带过，下次也不会有时间来补充了。

不过要是遇到合适的问题，我觉得我还是会在其他问题里讲一点自己浅薄的认识。

量子场论是什么？

量子场论开放分类：物理量子场论量子场论是量子力学和经典场论相结合的物理理论，已被广泛的应用于粒子物理学和凝聚态物理学中。

量子场论为描述多粒子系统，尤其是包含粒子产生和湮灭过程的系统，提供了有效的描述框架。非相对论性的量子场论主要被应用于凝聚态物理学，比如描述超导性的BCS理论。

而相对论性的量子场论则是粒子物理学不可或缺的组成部分。自然界目前人类所知的有四种基本相互作用：强作用，电磁相互作用，弱作用，引力。除去引力，另三种相互作用都找到了合适满足特定对称性的量子场论来描述。

强作用有量子色动力学（QCD，QuantumChromodynamics)；电磁相互作用有量子电动力学（QED,QuantumElectrodynamics)，理论框架建立于1920到1950年间，主要的贡献者为保罗·狄拉克，弗拉迪米尔·福克，沃尔夫冈·泡利，朝永振一郎，施温格，理查德·费曼和迪森等；弱作用有费米点作用理论。

后来弱作用和电磁相互作用实现了形式上的统一，通过希格斯机制（HiggsMechanism）产生质量，建立了弱电统一的量子规范理论，即GWS（Glashow,Weinberg,Salam）模型。

量子场论成为现代理论物理学的主流方法和工具。所谓“量子场论”的学科是从狭义相对论和量子力学的观念的结合而产生的。

它和标准（亦即非相对论性）的量子力学的差别在于，任何特殊种类的粒子的数目不必是常数。每一种粒子都有其反粒子（有时，诸如光子，反粒子和原先粒子是一样的）。

一个有质量的粒子和它的反粒子可以湮灭而形成能量，并且这样的对子可由能量产生出来。的确，甚至粒子数也不必是确定的；因为不同粒子数的态的线性叠加是允许的。

最高级的量子场论是“量子电动力学”--基本上是电子和光子的理论。该理论的预言具有令人印象深刻的精确性（例如，上一章已提到的电子的磁矩的精确值，参阅177页）。

然而，它是一个没有整理好的理论--不是一个完全协调的理论--因为它一开始给出了没有意义的“无限的”答案，必须用称为“重正化”的步骤才能把这些无限消除。并不是所有量子场论都可以用重正化来补救的。

即使是可行的话，其计算也是非常困难的。使用“路径积分”是量子场论的一个受欢迎的方法。

它是不仅把不同粒子态（通常的波函数）而且把物理行为的整个空间--时间历史的量子线性叠加而形成的（参阅费因曼1985年的通俗介绍）。

但是，这个方法自身也有附加的无穷大，人们只有引进不同的“数学技巧”才能赋予意义。

尽管量子场论勿庸置疑的威力和印象深刻的精确度（在那些理论能完全实现的很少情况），人们仍然觉得，必须有深刻的理解，才能相信它似乎是导向“任何物理实在的图像”。

物理九大基本学科

力学声学热学分子物理学电磁学光学原子物理学原子核物理学固体物理学物理学是研究物质的结构、相互作用和运动规律以及它们的各种实际应用的科学。它是自然科学的基础，是近代科学技术的主要源泉。

物理学是一门基础学科。

在物理学研究过程中形成和发展起来的基本概念、基本理论、基本实验手段和精密测量方法，不但成为其它学科诸如天文学、化学、生物学、地学、医学、农业科学和计量学等学科的组成部分，还推动了这些学科的发展。

物理学还与其它学科相互渗透，产生了一系列交叉学科，如化学物理、生物物理、大气物理、海洋物理、地球物理、天体物理等。物理学也是各种技术学科和工程学科的共同基础。

在近代物理发展的基础上，产生了许多新的技术学科，如核能与其它能源技术，半导体电子技术，材料科学等，从而有力的促进了生产技术的发展和变革。

19世纪以来，人类历史上的四次产业革命和工业革命都是以对物理某些领域的基本规律认识的突破为前提的。

当代，物理学科研究的突破不断导致各种高新技术的产生和发展，从而在近代物理学与许多高科技学科之间形成一片相互交叠的基础性研究与应用性研究相结合的宽广领域。

物理学科与技术学科各自根据自身的特点，从不同的角度对这些领域的研究，既促进了物理学的发展和应用，又促进了高科技的发展和提高。

通常根据研究的物质运动形态和具体对象不同，物理学可主要分为如下几个二级学科：理论物理、粒子物理与原子核物理、原子与分子物理、凝聚态物理、等离子体物理、声学、光学以及无线电物理，本专业的主要涉及光学、凝聚态物理和理论物理三个二级学科十学科方向。

主要研究方向及其内容：1．光信息存储与显示（光学）X射线影像存储材料和电子俘获光存储材料的制备、性能、存储机理及其应用的研究；有机、无机电致发光材料的制备、传输机制、激发态过程的机理及其显示器件的研究。

2．光电子材料与器件物理（光学）研究稀土发光、半导体发光、阴极射线发光、高能射线发光、上转换发光、长余辉发光、白光LED照明、无汞荧光灯、光学薄膜基本设计、超声、光存储、有机发光、载流子传输材料、有机光致发光和电致发光材料等的制备；研究光致发光和电致发光机理、载流子传输机制等；研究发光二极管、无机有机薄膜电致发光器件、厚膜交/直流驱动软屏、电子油墨（或电子纸）、光电探测器等光电子器件；研究这些材料和器件的新技术和新工艺以及它们的应用。

3．激光与光电检测技术（光学）主要研究各种激光与光电检测方法、技术及其应用，包括激光干涉测量技术、光电传感技术、激光超声技术、激光多普勒振动检测技术、红外检测技术、激光扫描测量技术及微纳米测量技术等。

此外常规的无损检测手段中光电技术的使用也是本领域的研究内容之一。4．光信息传输与光信号处理（光学）研究光在各种光纤和各种光波导中的传输特性，以及由它们构成的光纤通信系统与光纤传感系统。

包括导波光学、非线性光纤光学、光纤通信系统；以及利用光纤构成的传感系统，比如电压、电流、气体等传感器和智能蒙皮、分布传感系统、生物光纤传感器等。并涉及到全光网络、全光信号处理等方面的研究课题。

5．光物理（光学）本研究方向在激光与原子、分子、团簇及凝聚态物质的相互作用、光学超快现象、光与生物体相互作用和THZ光的理论和应用等前沿课题上开展深入系统的研究。

研究领域涉及激光与物质的相互作用及其用于激光探测等基础研究和应用基础研究，希望在非线性光学、激光与原子分子相互作用、OCT、超快光物理、有机聚合物的光子学和THz物理等研究方面取得突破性的进展，开拓和发展若干新的研究方向，为国家经济建设服务。

6．稀土物理（凝聚态物理）本方向研究凝聚态物质中稀土离子的能级和激发态过程。

当前研究的主要方向是稀土离子高能激发态的结构，辐射跃迁，无辐射跃迁，电子--声子偶合，组合混杂，真空紫外激发的稀土发光材料中的物理问题。

7．纳米结构与低维物理（凝聚态物理）低维体系是研究小空间尺度的新的物理效应，已成为凝聚态物理最活跃和最富有生命力的重要前言领域之一，它与物理、化学、生物、医药学、材料、电子学、光电子学、磁学、能源和环境等多学科交叉，该体系的能带可人工剪裁性、表面界面效应、量子尺寸效应、隧穿效应等赋予它许多原来三维固体不具备的、内涵丰富而深刻的新现象、新效应、新规律，并广泛地被用来开发具有新原理、新结构的固态电子、光电子器件。

8．固体发光（凝聚态物理）固体发光是固体光学的一个重要组成部分，它是物体将吸收的能量转化为光辐射的过程。它主要包括：光致发光、阴极射线发光、高能射线发光、电致发光和生物发光等。

固体发光有很多重要的应用，例如：照明光源、阴极射线等各种发光显示器、高密度光存储材料、核辐射探测等。近年来固体光学又有很多新的发展，诸如有机电致发光、多孔硅、低维体系、量子剪裁等。

本研究方向瞄准学科前沿，主要开展了无机及有机电致发光材料及机理、发光存储材料及机理、上转换材料及机理等诸多有特色的研究工作。

9．数学物理与计算物理（理论物理）数学物理学是以研究物理问题为目标的数学理论和数学方法。它探讨物理现象的数学模型，即寻求物理现象的数学描述和诠释和。

从二十世纪开始，由于物理学内容的更新，数学物理也有了新的面貌。伴随着对电磁理论，量子理论和引力场的深入研究，人们的时空观念发生了根本的变化，数学物理成为研究物理现象的有力工具。

随着电子计算机的发展，数学物理中的许多问题可以通过数值计算来解决，由此发展起来的计算物理都发挥着越来越大的作用。计算机直接模拟物理模型也成为重要的方法。

本研究方向主要研究广义相对论和宇宙学，数学物理的几何结构，大型物理体系的数值计算和并行算法等。

10．凝聚态理论（理论物理）理论物理的一个重要分支是凝聚态物理中的量子多体理论，它是应用现代多体理论和量子场论研究凝聚态物理中的新现象、揭示新现象中的物理本质。

当前研究的主要方向：计算凝聚态物理，强关联电子系统和介观体系中的物理问题，低维量子系统中的电声相互作用，凝聚物质中的量子输运理论，以及非费米液体、自旋输运和Mott相变等。

量子物理、量子力学、量子场论 有什么区别

。

量子物理是对整个近现代物理的一种称呼吧，因为研究范围和尺度到了微观量级，也就是普朗克常量的量级，比如量子光学，量子信息等等；量子力学是研究微观世界的一种方法，基础是薛定谔方程，研究微观世界动力学演化过程；量子场论结合了量子力学和经典场论，提出物质世界是由场构成的观点，并以此展开对电磁相互作用，弱相互作用和强相互作用的研究，在场论理论中，相互作用就是场的耦合，粒子就是场的激发态。

看懂文小刚做的东西需要哪些数学和物理的知识？

如果要看懂文小刚做的东西，需要数学的二次定理和物理的量子学，我虽然没有读懂过，但是他的教科书《量子多体理论》包含了许多他自己的私人想法。

就个人而言，这本书很难阅读，且跳跃性强，特别是对于那些缺乏领域理论基础的学生来说，是很难看懂的，反正我个人是看不懂的。毕竟，这本书不是场论的教科书，而是在凝聚态中的应用。

因此，在学习之前，我们需要具有良好的量子场论基础，至少必须详细理解相关概念。当然，这需要很长时间。文小刚的工作是超越兰道理论的重要突破。

在这本书中，许多地方都注意与凝聚态物理的基本概念进行类比，例如准粒子和基本激发。但是，介绍相对简短。文小刚对称破坏理论和费米液体理论是必要的。

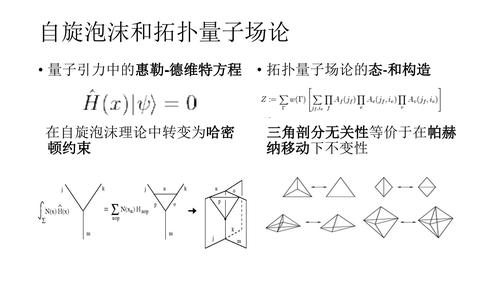
我个人认为在阅读之前，要对于数学和物理的基本知识掌握完全，在去读这些作品会很好。文小刚的拓扑顺序理论与分数量子霍尔有密切的联系，因此了解量子霍尔效应也是必不可少的。

而且文小刚的演讲非常好，他的演讲对于量子场论也有这方面的研究。通过量子霍尔效应的有效理论，讨论如何获得分数电荷或某些东西，这是本书的主要亮点，至少没有其他量子场论书籍看到过类似的东西。

建议在阅读文小刚的东西之前，可以了解一些有关此的知识。总之，阅读本书需要大量的背景知识和基础知识。尽管本书有中文版本，但要自己学习并不容易。

这可能也是因为文小刚自主学习的能力吧，一般人反正是看不懂的，我在看这些作品的时候都感觉大云里雾里的，不知道其他人有没有这样的想法。

理论物理包括哪些？ 详细 谢谢！

1．学科研究范围理论物理是在实验现象的基础上，以理论的方法和模型研究基本粒子、原子核、原子、分子、等离子体和凝聚态物质运动的基本规律，解决学科本身和高科技探索中提出的基本理论问题。

研究范围包括粒子物理理论、原子核理论、凝聚态理论、统计物理、光子学理论、原子分子理论、等离子体理论、量子场论与量子力学、引力理论、数学物理、理论生物物理、非线性物理、计算物理等。

2．课程设置高等量子力学、高等统计物理、量子场论、群论、规范场论、现代数学方法、计算物理、凝聚态理论、量子多体理论、粒子物理、核理论、非平衡统计物理、非线性物理、广义相对论、量子光学、理论生物物理、天体物理、微分几何、拓扑学等。