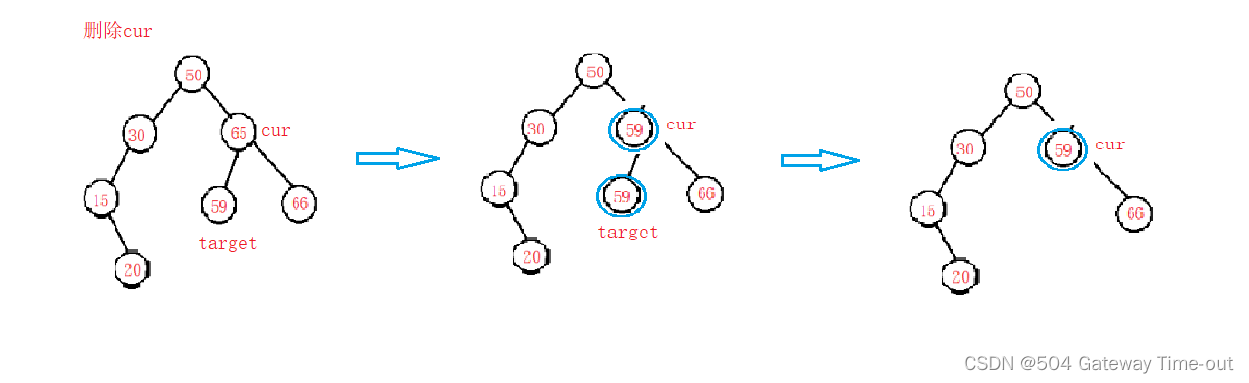
def fun(n):print(n)while n != 1:n = 3 * n + 1 if n % 2 else n / 2print('finished')for i in range(2,1000):fun(i)

1、了解了什么是"角谷猜想"

    对于任意一个自然数n,若n为偶数,则将其除以2;若n为奇数,则将其乘以3,然后再加1。如此经过有限次运算后,总可以得到自然数1。

2、了解了迭代算法的原理

    迭代算法（Iteration）是用计算机处理问题的一种基本方法。它利用计算机运算速度快、存储容量大、适合做重复性操做的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推导出它的一个新值。迭代法是一种不断用变量的旧值递推出新值的解决问题的方法。

    迭代算法的步骤：

    （1） 确定迭代变量

    （2） 建立迭代关系式

    （3）对迭代过程进行控制式

3、掌握了如何使用迭代算法解决"角谷猜想"问题

    （1）确定迭代变量n（即>2的自然数）

for i in range(2,1000):#这里以2-999为例

    （2）确定迭代关系式：当n为偶数时,n = n/2;当n为奇数时,n =n*3+1。

n = 3 * n + 1 if n % 2 else n / 2

    （3）建立迭代过程控制式：这里结束迭代过程的条件即为经过x运算后，n==1，则结束迭代过程。

while n != 1:

​4、实验结果

 

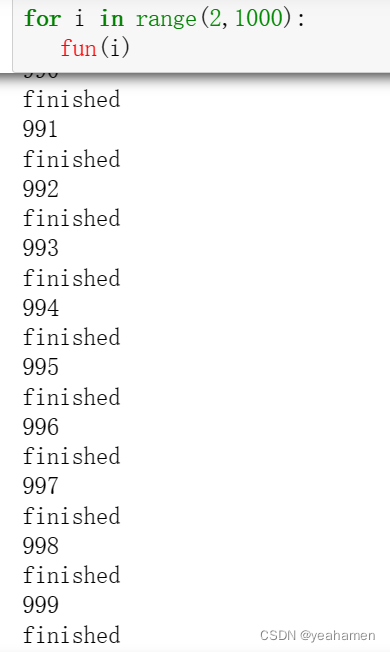
通过观察可以发现2-999数字均符合角谷猜想。