题目描述：

题目传送门

---

解题思路：

根据数据范围以及题目中提到的合并等操作可以联想用并查集求解。
但是仔细想想，普通并查集只能判断某元素是否为统一集合的联通性问题，而题目中提到了“战舰数量”等权值性的问题，这种时候我们就要对并查集进行一些改变，成为可以处理权值的带权并查集。

• 带权并查集

必须要了解的前置知识是并查集（废话），百度食用更佳。

带权并查集其实和普通并查集没有本质的区别，仅仅只是需要在路径压缩或合并集合的时候维护或更新节点与父节点的边权关系以及维护该集合内元素个数。

设 $f{a}_x$ 表示从 $x$ 到 $x$ 的父节点的边权，$di{s}_x$ 表示从 $x$ 到达 $f{a}_x$ 的边权，$cn{t}_x$ 表示为元素 $x$ 所在的集合的元素个数。

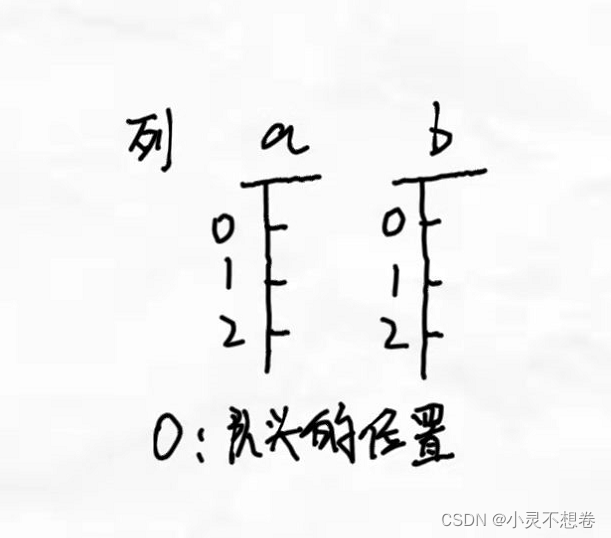
1. 考虑合并集合 $a$ 与 $b$ ，我们可以让集合 $a$ 的根节点与集合 $b$ 的根节点相连，这样 $a$ 就成为了 $b$ 的一颗子树。可以的之，连接后 $a$ 子树的深度肯定是位于原本 $b$ 所有子树的下方，也就是说，$a$ 的根节点 $x$ 到大 $b$ 的根节点 $y$ 的距离是原本 $b$ 子树的元素个数，也就是说 $di{s}_x=cn{t}_y$。也很容易理解，由于加上了子树 $a$，那么 $b$ 的元素个数为 $cn{t}_x+cn{t}_y$
2. 考虑路径压缩操作，所有节点的父亲都为跟，也就是说我们要维护使得所有节点与根的边权不变。操作后，$f{a}_x$ 节点的父亲变为集合的根，也就是说 $f{a}_{f{a}_x}$ 是这个集合的跟，那么 $x$ 点到达根的距离为：$di{s}_x=di{s}_x+di{s}_{f{a}_x}$。这句话的解析其实就是该节点到达父节点的距离，再加上父节点到达根的距离，即为该节点到达根的距离。

带权并查集的查询：

int find(int x)
{if(fa[x]==x) return x;int t=find(fa[x]);  //必须要有这么一赋值步骤，因为复制中find函数已经运行过一次了，此时 fa[fa[x]]为根节点，与分析相符；否则 fa[fa[x]]未经过改变，不为根节点，与分析不符dis[x]+=dis[fa[x]];  //更新当前点到根节点的距离fa[x]=t;return fa[x];
}

关于赋值操作的必要性请看此贴

合并集合操作：

void join(int x,int y)
{int a=find(x),b=find(y);fa[a]=b;dis[a]=cnt[b];  //更新根节点之间的距离cnt[b]+=cnt[a];  //更新集合元素个数cnt[a]=cnt[b];
}

知道了带权并查集的思想，这道题就不难解除。

---

CODE:

#include <iostream>
#include <cmath>
using namespace std;
int n;
int fa[50010],dis[50010]={0},cnt[50010];
int find(int x)
{if(fa[x]==x) return x;int t=find(fa[x]); dis[x]+=dis[fa[x]];fa[x]=t;return fa[x];
}
void join(int x,int y)
{int a=find(x),b=find(y);fa[a]=b;dis[a]=cnt[b];cnt[b]+=cnt[a];cnt[a]=cnt[b];
}
int main()
{std::ios::sync_with_stdio(false);  //关闭输入输出同步流cin>>n;char pos;int a,b;for(int i=1;i<=30000;i++) fa[i]=i,cnt[i]=1;for(int i=1;i<=n;i++){cin>>pos>>a>>b;if(pos=='M'){if(find(a)!=find(b))join(a,b);}if(pos=='C'){if(find(a)!=find(b)) cout<<-1<<endl;else cout<<abs(dis[a]-dis[b])-1<<endl;}}return 0;
}