目录
- 刚体的定轴转动 力矩
- 刚体
- 刚体转动的角速度和角加速度
- 匀变速转动公式
- 角量与线量的关系
- 力矩
- 转动惯量 转动定律
- 质点的转动惯量
- 角动量 角动量守恒定律
- 角动量
- 刚体定轴转动的角动量
- 力矩做功 刚体定轴转动的动能定理
- 力矩做功
- 刚体绕定轴转动的动能定理
刚体的定轴转动 力矩
刚体
刚体的定义:在外力作用下,形状和大小都不发生改变的物体。
刚体的运动形式包括平动和转动。
平动:刚体中所有点的运动轨迹都保持相同,各点运动状态一样(如v,a),此时,刚体上任意一点的运动可以代表整个刚体的运动。
刚体转动的角速度和角加速度

角坐标: θ = θ ( t ) \theta =\theta (t) θ=θ(t)
逆时针: θ > 0 \theta >0 θ>0,顺时针: θ < 0 \theta<0 θ<0
角位移: Δ θ = θ ( t + Δ t ) − θ ( t ) \Delta \theta = \theta (t+\Delta t)-\theta (t) Δθ=θ(t+Δt)−θ(t)
角速度矢量: ω = lim Δ t → 0 Δ θ Δ t = d θ d t \omega = \lim_{\Delta t\to 0}\frac{\Delta \theta}{\Delta t}=\frac{d\theta}{dt} ω=Δt→0limΔtΔθ=dtdθ ω \omega ω方向:右手螺旋方向。

刚体定轴转动(一维转动)的转动方向可以用角速度的正负表示。
角加速度: α ⃗ = d ω ⃗ d t \vec{\alpha}=\frac{d\vec{\omega}}{dt} α=dtdω
匀变速转动公式
当刚体绕定轴转动的 α \alpha α=常量时,刚体做匀变速转动。
| 质 点 \red{质点} 质点匀变速直线运动 | 刚 体 \red{刚体} 刚体绕定轴匀变速转动 |
|---|---|
| v = v 0 + a t v=v_0+at v=v0+at | ω = ω 0 + α t \omega = \omega _0+\alpha t ω=ω0+αt |
| x = x 0 + v 0 t + 1 2 a t 2 x=x_0+v_0t+\frac{1}{2}at^2 x=x0+v0t+21at2 | θ = θ 0 + ω 0 t + 1 2 α t 2 \theta = \theta _0+\omega _0t+\frac{1}{2}\alpha t^2 θ=θ0+ω0t+21αt2 |
| v 2 = v 0 2 + 2 a ( x − x 0 ) v^2=v_0^2+2a(x-x_0) v2=v02+2a(x−x0) | ω 2 = ω 0 2 + 2 α ( θ − θ 0 ) \omega ^2=\omega _0^2+2\alpha (\theta -\theta _0) ω2=ω02+2α(θ−θ0) |
角量与线量的关系

(1) v ⃗ = r ω e ⃗ t \vec{v}=r\omega \vec{e}_t v=rωet
(2) a t = r α , a n = r ω 2 a_t=r \alpha,a_n=r\omega ^2 at=rα,an=rω2
力矩

力矩是用来描述力对刚体的转动作用的物理量。
F ⃗ \vec{F} F对转轴z的力矩定义为: M ⃗ = r ⃗ × F ⃗ → M = F r s i n θ = F d \vec{M}=\vec{r} \times \vec{F} \to M= Frsin\theta = Fd M=r×F→M=Frsinθ=Fd其中d是力臂。
转动惯量 转动定律
质点的转动惯量

设单个质点 m m m与转轴刚性连接
M = r F s i n θ = r F t = r ( m a t ) = r m ( r α ) = m r 2 α = J α M=rFsin\theta = rF_t=r(ma_t)=rm(r\alpha)=mr^2\alpha = J\alpha M=rFsinθ=rFt=r(mat)=rm(rα)=mr2α=Jα定义: J = m r 2 J=mr^2 J=mr2为质点 m m m对 O O O的“转动惯量”
转动定律:刚体定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比。
J = ∑ j Δ m j r j 2 ; J = ∫ r 2 d m J=\sum_j \Delta m_jr_j^2;J=\int r^2dm J=j∑Δmjrj2;J=∫r2dm
(1) M = 0 , ω 不 变 M=0,\omega 不变 M=0,ω不变
(2) α ∝ M J \alpha \propto \frac{M}{J} α∝JM
(3) M = J α = J d ω d t M=J\alpha = J\frac{d\omega}{dt} M=Jα=Jdtdω
说 明 : \red{说明:} 说明:
(1) M M M与 α \alpha α方向相同
(2)为瞬时关系
(3)转动中 M = J α M=J\alpha M=Jα与平动中 F = m a F=ma F=ma地位相同。
角动量 角动量守恒定律
角动量

质点的运动描述: p ⃗ = m v ⃗ , E k = m v 2 / 2 \vec{p}=m\vec{v},E_k=mv^2/2 p=mv,Ek=mv2/2
刚体定轴转动描述: L = J ω , E k = J ω 2 / 2 L=J\omega,E_k=J\omega ^2/2 L=Jω,Ek=Jω2/2
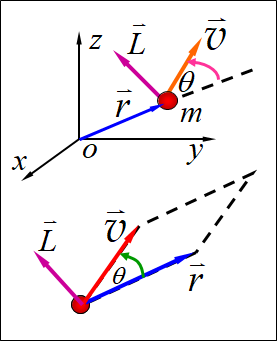
角动量定义:质量为 m m m的质点以速度 v ⃗ \vec{v} v在空间运动,某一时刻对O的位矢为 r ⃗ \vec{r} r,则质点对O的角动量定义为:
L ⃗ = r ⃗ × p ⃗ = r ⃗ × m v ⃗ \vec{L}=\vec{r} \times \vec{p}=\vec{r}\times m\vec{v} L=r×p=r×mv 大 小 : L = r m v s i n θ 大小:L=rmvsin\theta 大小:L=rmvsinθ
L ⃗ \vec{L} L的方向符合右手法则,角动量单位: k g ⋅ m 2 ⋅ s − 1 kg\cdot m^2\cdot s^{-1} kg⋅m2⋅s−1
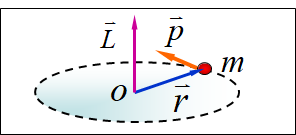
如图:质点以 ω \omega ω作半径为 r r r的圆周运动,相对于圆心的角动量为: L = m r 2 ω = J ω L=mr^2\omega = J\omega L=mr2ω=Jω
质点的角动量定理: M ⃗ = d L ⃗ d t = r ⃗ × F ⃗ \vec{M}=\frac{d\vec{L}}{dt}=\vec{r}\times \vec{F} M=dtdL=r×F
作 用 于 质 点 的 合 外 力 对 参 考 点 O 的 力 矩 , 等 于 质 点 对 该 点 O 的 角 动 量 随 时 间 的 变 化 率 。 \green{作用于质点的合外力对参考点O的力矩,等于质点对该点O的角动量随时间的变化率。} 作用于质点的合外力对参考点O的力矩,等于质点对该点O的角动量随时间的变化率。
又可得冲量矩:
M ⃗ d t = d L ⃗ ⇒ 冲 量 矩 : ∫ t 1 t 2 M ⃗ d t = L ⃗ 2 − L ⃗ 1 \vec{M}dt=d\vec{L}\Rightarrow 冲量矩:\int_{t_1}^{t_2}\vec{M}dt=\vec{L}_2-\vec{L}_1 Mdt=dL⇒冲量矩:∫t1t2Mdt=L2−L1
所以质点的角动量定理又可以表述为: 对 同 一 参 考 点 O , 质 点 所 受 的 冲 量 矩 等 于 质 点 角 动 量 的 增 量 。 \green{对同一参考点O,质点所受的冲量矩等于质点角动量的增量。} 对同一参考点O,质点所受的冲量矩等于质点角动量的增量。
由上式可知:
如果 M ⃗ = 0 , 则 L ⃗ = r ⃗ × m v ⃗ = 恒 矢 量 \vec{M} =0,则\vec{L}=\vec{r}\times m\vec{v}=恒矢量 M=0,则L=r×mv=恒矢量
即:质点的角动量守恒定律: 若 质 点 所 受 合 外 力 对 某 给 定 点 O 的 力 矩 为 0 , 则 质 点 对 O 点 的 角 动 量 保 持 不 变 \red{若质点所受合外力对某给定点O的力矩为0,则质点对O点的角动量保持不变} 若质点所受合外力对某给定点O的力矩为0,则质点对O点的角动量保持不变
刚体定轴转动的角动量
M ⃗ d t = d L ⃗ = d ( J ω ⃗ ) ⇒ ∫ t 1 t 2 = J ω 2 − J ω 1 \vec{M}dt=d\vec{L}=d(J\vec{\omega})\Rightarrow \int_{t_1}^{t_2}=J\omega _2-J\omega _1 Mdt=dL=d(Jω)⇒∫t1t2=Jω2−Jω1
定轴转动刚体的角动量定理:转动物体所受合外力矩的冲量等于在这段时间内转动物体角动量的增量。
若 M = 0 , 则 L = J ω = 常 量 若M=0,则L=J\omega =常量 若M=0,则L=Jω=常量
定轴转动刚体的角动量守恒定律: 如果物体所受合外力矩等于0,或者不受外力矩的作用,物体的角动量保持不变。
力矩做功 刚体定轴转动的动能定理
力矩做功

d W = F ⃗ ⋅ d r ⃗ = F c o s φ ∣ d r ∣ = F t d s = F t r d θ = M d θ dW=\vec{F}\cdot d\vec{r}=Fcos\varphi |dr|=F_tds=F_trd\theta =Md\theta dW=F⋅dr=Fcosφ∣dr∣=Ftds=Ftrdθ=Mdθ ⇒ 力 矩 的 功 : W = ∫ θ 1 θ 2 M d θ \Rightarrow力矩的功:W=\int_{\theta _1}^{\theta _2}Md\theta ⇒力矩的功:W=∫θ1θ2Mdθ
说 明 : \red{说明:} 说明:所谓力矩做功,实质上韩式力的功,并无任何关于力矩的功的新的定义,只是在刚体转动中,用力矩和角位移的积来表示更为方便而已。
力矩的功率: P = d W d t = M d θ d t = M ω P=\frac{dW}{dt}=M\frac{d\theta}{dt}=M\omega P=dtdW=Mdtdθ=Mω 比 较 : W = ∫ F ⃗ ⋅ d r ⃗ ; P = F ⃗ . v ⃗ 比较:W=\int \vec{F}\cdot d\vec{r};P=\vec{F}.\vec{v} 比较:W=∫F⋅dr;P=F.v
当 M ⃗ \vec{M} M与 ω ⃗ \vec{\omega} ω同方向, W W W和 P P P为正
当 M ⃗ \vec{M} M与 ω ⃗ \vec{\omega} ω反方向, W W W和 P P P为负
转动动能: E k = ∑ i 1 2 Δ m i v i 2 = 1 2 ( ∑ i Δ m i v i 2 ) ω 2 = 1 2 J ω 2 − − − − − − ( 和 E k = 1 2 m v 2 ) 比 较 E_k=\sum_i\frac{1}{2}\Delta m_iv_i^2=\frac{1}{2}(\sum_i \Delta m_iv_i^2)\omega ^2=\frac{1}{2}J\omega ^2------(和E_k=\frac{1}{2}mv^2)比较 Ek=i∑21Δmivi2=21(i∑Δmivi2)ω2=21Jω2−−−−−−(和Ek=21mv2)比较
刚体绕定轴转动的动能定理
W = ∫ θ 1 θ 2 M d t = ∫ θ 1 θ 2 J d ω d t d θ = ∫ ω 1 ω 2 J ω d ω = 1 2 J ω 2 2 − 1 2 J ω 1 2 W=\int_{\theta _1}^{\theta _2}Mdt=\int_{\theta _1}^{\theta _2}J\frac{d\omega}{dt}d\theta=\int_{\omega _1}^{\omega _2}J\omega d\omega=\frac{1}{2}J\omega_2^2-\frac{1}{2}J\omega_1^2 W=∫θ1θ2Mdt=∫θ1θ2Jdtdωdθ=∫ω1ω2Jωdω=21Jω22−21Jω12
比较: W = ∫ F ⃗ d r ⃗ = 1 2 m v 2 2 − 1 2 m v 1 2 W=\int \vec{F}d\vec{r}=\frac{1}{2}mv_2^2-\frac{1}{2}mv_1^2 W=∫Fdr=21mv22−21mv12





