试商法
采用试商法实现除法运算,对于32位的除法,需要至少32个时钟周期才能得到除法结果。下面是试商法的一般过程。
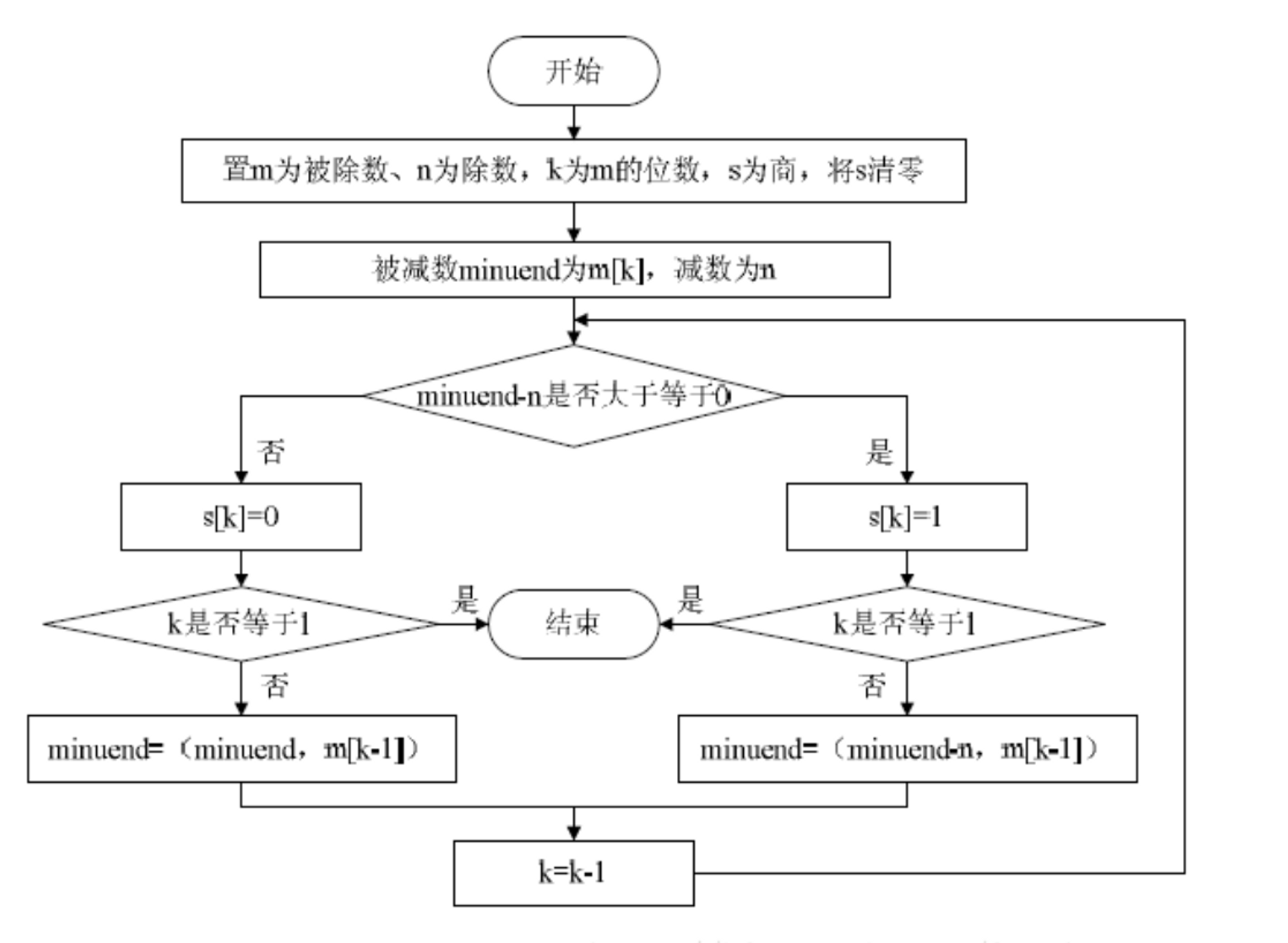
设被除数是m,除数是n,商保存在s中,被除数的位数是k,其计算步骤如下(为了便于说明,在此处将所有数据的最低位称为第1位,而不称为第0位)。
1、取出被除数的最高位m[k],使用被除数的最高位减去除数n,如果结果大于等于0,则商的s[k]为1,反之为0。
2、如果上一步得出的结果是0,表示当前的被减数小于除数,则取出被除数剩下的值的最高位m[k-1],与当前被减数组合做为下一轮的被减数;如果上一步得出的结果是1,表示当前的被减数大于除数,则利用上一步中减法的结果与被除数剩下的值的最高位m[k-1]组合做为下一轮的被减数。然后,设置k等于k-1。
3、新的被减数减去除数,如果结果大于等于0,则商的s[k]为1,否则s[k]为0,后面的步骤重复2-3,直到k等于1。
其他
- 该方法对于有符号数和无符号数除法均适用,对于有符号数需要处理符号位,最后在运算结果中添加符号位
- 在处理器中,除法运算需要多个周期才能完成,需要注意暂停流水线
除法器设计
单步运算设计
单步除法计算时,单步被除数位宽(信号 dividend)需比原始除数(信号 divisor)位宽多 1bit 才不至于溢出。
为了便于流水,输出端需要有寄存器来存储原始的除数(信号 divisor 和 divisor_kp)和被除数信息(信号 dividend_ci 和 dividend_kp)。
单步的运算结果就是得到新的 1bit 商数据(信号 merchant)和余数(信号 remainder)。
为了得到最后的除法结果,新的 1bit 商数据(信号 merchant)还需要与上一周期的商结果(merchant_ci)进行移位累加。
// parameter M means the actual width of divisor
module divider_cell#(parameter N=5,parameter M=3)(input clk,input rstn,input en,input [M:0] dividend,input [M-1:0] divisor,input [N-M:0] merchant_ci , //上一级输出的商input [N-M-1:0] dividend_ci , //原始除数output reg [N-M-1:0] dividend_kp, //原始被除数信息output reg [M-1:0] divisor_kp, //原始除数信息output reg rdy ,output reg [N-M:0] merchant , //运算单元输出商output reg [M-1:0] remainder //运算单元输出余数);always @(posedge clk or negedge rstn) beginif (!rstn) beginrdy <= 'b0 ;merchant <= 'b0 ;remainder <= 'b0 ;divisor_kp <= 'b0 ;dividend_kp <= 'b0 ;endelse if (en) beginrdy <= 1'b1 ;divisor_kp <= divisor ; //原始除数保持不变dividend_kp <= dividend_ci ; //原始被除数传递if (dividend >= {1'b0, divisor}) beginmerchant <= (merchant_ci<<1) + 1'b1 ; //商为1remainder <= dividend - {1'b0, divisor} ; //求余endelse beginmerchant <= merchant_ci<<1 ; //商为0remainder <= dividend ; //余数不变endend // if (en)else beginrdy <= 'b0 ;merchant <= 'b0 ;remainder <= 'b0 ;divisor_kp <= 'b0 ;dividend_kp <= 'b0 ;endendendmodule
顶层模块
将单步计算的余数(信号 remainder)和原始被除数(信号 dividend)对应位的 1bit 数据重新拼接,作为新的单步被除数输入到下一级单步除法计算单元。
其中,被除数、除数、及商的数据信息也要在下一级运算单元中传递。
//parameter N means the actual width of dividend
//using 29/5=5...4
module divider_man#(parameter N=5,parameter M=3,parameter N_ACT = M+N-1)(input clk,input rstn,input data_rdy , //数据使能input [N-1:0] dividend, //被除数input [M-1:0] divisor, //除数output res_rdy ,output [N_ACT-M:0] merchant , //商位宽:Noutput [M-1:0] remainder ); //最终余数wire [N_ACT-M-1:0] dividend_t [N_ACT-M:0] ;wire [M-1:0] divisor_t [N_ACT-M:0] ;wire [M-1:0] remainder_t [N_ACT-M:0];wire [N_ACT-M:0] rdy_t ;wire [N_ACT-M:0] merchant_t [N_ACT-M:0] ;//初始化首个运算单元divider_cell #(.N(N_ACT), .M(M))u_divider_step0( .clk (clk),.rstn (rstn),.en (data_rdy),//用被除数最高位 1bit 数据做第一次单步运算的被除数,高位补0.dividend ({{(M){1'b0}}, dividend[N-1]}),.divisor (divisor), .merchant_ci ({(N_ACT-M+1){1'b0}}), //商初始为0.dividend_ci (dividend[N_ACT-M-1:0]), //原始被除数//output.dividend_kp (dividend_t[N_ACT-M]), //原始被除数信息传递.divisor_kp (divisor_t[N_ACT-M]), //原始除数信息传递.rdy (rdy_t[N_ACT-M]),.merchant (merchant_t[N_ACT-M]), //第一次商结果.remainder (remainder_t[N_ACT-M]) //第一次余数);genvar i ;generatefor(i=1; i<=N_ACT-M; i=i+1) begin: sqrt_stepxdivider_cell #(.N(N_ACT), .M(M))u_divider_step(.clk (clk),.rstn (rstn),.en (rdy_t[N_ACT-M-i+1]),.dividend ({remainder_t[N_ACT-M-i+1], dividend_t[N_ACT-M-i+1][N_ACT-M-i]}), //余数与原始被除数单bit数据拼接.divisor (divisor_t[N_ACT-M-i+1]),.merchant_ci (merchant_t[N_ACT-M-i+1]),.dividend_ci (dividend_t[N_ACT-M-i+1]),//output.divisor_kp (divisor_t[N_ACT-M-i]),.dividend_kp (dividend_t[N_ACT-M-i]),.rdy (rdy_t[N_ACT-M-i]),.merchant (merchant_t[N_ACT-M-i]),.remainder (remainder_t[N_ACT-M-i]));end // block: sqrt_stepxendgenerateassign res_rdy = rdy_t[0];assign merchant = merchant_t[0]; //最后一次商结果作为最终的商assign remainder = remainder_t[0]; //最后一次余数作为最终的余数endmodule
testbench
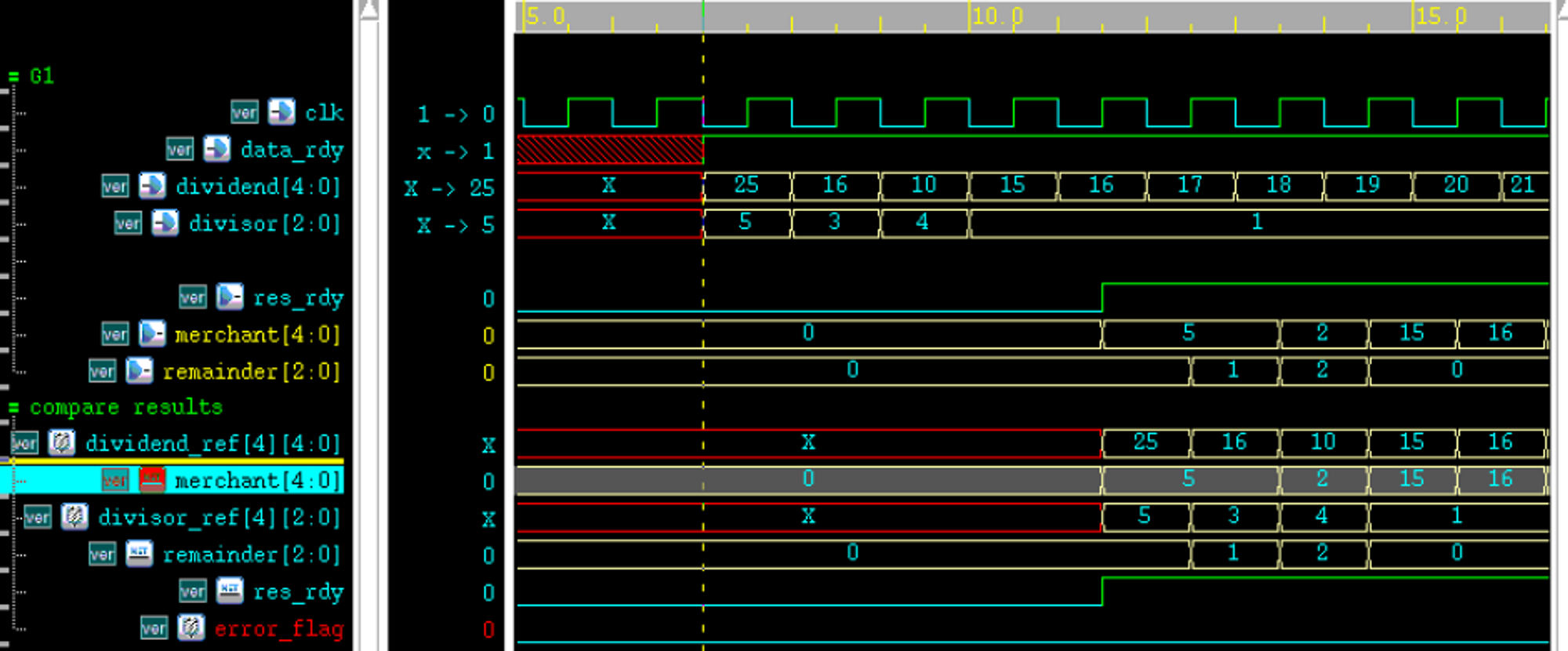
取被除数位宽为 5,除数位宽为 3,testbench 中加入自校验,描述如下:
`timescale 1ns/1nsmodule test ;parameter N = 5 ;parameter M = 3 ;reg clk;reg rstn ;reg data_rdy ;reg [N-1:0] dividend ;reg [M-1:0] divisor ;wire res_rdy ;wire [N-1:0] merchant ;wire [M-1:0] remainder ;//clockalways beginclk = 0 ; #5 ;clk = 1 ; #5 ;end//driverinitial beginrstn = 1'b0 ;#8 ;rstn = 1'b1 ;#55 ;@(negedge clk ) ;data_rdy = 1'b1 ;dividend = 25; divisor = 5;#10 ; dividend = 16; divisor = 3;#10 ; dividend = 10; divisor = 4;#10 ; dividend = 15; divisor = 1;repeat(32) #10 dividend = dividend + 1 ;divisor = 7;repeat(32) #10 dividend = dividend + 1 ;divisor = 5;repeat(32) #10 dividend = dividend + 1 ;divisor = 4;repeat(32) #10 dividend = dividend + 1 ;divisor = 6;repeat(32) #10 dividend = dividend + 1 ;end//对输入延迟,便于数据结果同周期对比,完成自校验reg [N-1:0] dividend_ref [N-1:0];reg [M-1:0] divisor_ref [N-1:0];always @(posedge clk) begindividend_ref[0] <= dividend ;divisor_ref[0] <= divisor ;endgenvar i ;generatefor(i=1; i<=N-1; i=i+1) beginalways @(posedge clk) begindividend_ref[i] <= dividend_ref[i-1];divisor_ref[i] <= divisor_ref[i-1];endendendgenerate//自校验reg error_flag ;always @(posedge clk) begin# 1 ;if (merchant * divisor_ref[N-1] + remainder != dividend_ref[N-1] && res_rdy) beginb //testbench 中可直接用乘号而不考虑运算周期error_flag <= 1'b1 ;endelse beginerror_flag <= 1'b0 ;endend//module instantiationdivider_man #(.N(N), .M(M))u_divider(.clk (clk),.rstn (rstn),.data_rdy (data_rdy),.dividend (dividend),.divisor (divisor),.res_rdy (res_rdy),.merchant (merchant),.remainder (remainder));//simulation finishinitial beginforever begin#100;if ($time >= 10000) $finish ;endendendmodule // test
仿真结果