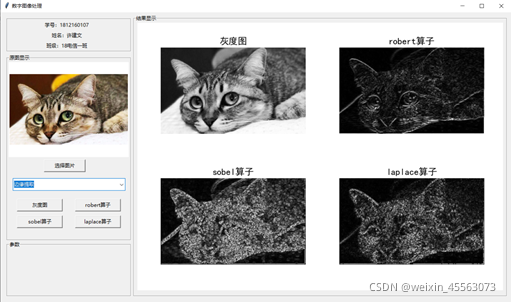
正版链接:https://blog.csdn.net/meenr/article/details/117605883
MATLAB实现图像复原
实验3、MATLAB实现图像复原
目录
- 实验3、MATLAB实现图像复原
- 1. 实验目的
- 2. 实验内容
- 3. MATLAB程序代码
- 4. 结果及分析
- 5. 典型的图像复原方法及其适用范围
- 6. MATLAB程序代码
- 途径一
- 途径二
1. 实验目的
(1)理解退化模型。
(2)掌握常用的图像复原方法。
2. 实验内容
(1)选择一幅清晰的灰度图像,对该图像进行模糊化处理,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对模糊图像进行复原,比较各种图像复原方法的复原效果。
(2)选择一幅清晰的灰度图像,对该图像进行模糊化处理并加入不同强度的高斯噪声,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对退化图像进行复原,比较各种图像复原方法的复原效果。
3. MATLAB程序代码
(1)选择一幅清晰的灰度图像,对该图像进行模糊化处理,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对模糊图像进行复原。
(2)选择一幅清晰的灰度图像,对该图像进行模糊化处理并加入高斯噪声,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对退化图像进行复原。
4. 结果及分析
(1)本实验选择一幅清晰的灰度图像,对该图像进行模糊化处理,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对模糊图像进行复原。原图像及其模糊化处理后的图像如图1所示。
模糊化应用点扩散函数fspecial('motion', LEN, THETA),以某一个角度逆时针旋转一定像素。函数中参数"LEN"是旋转的像素值,"THETA"为旋转角度。

对模糊化的图像用噪信比滤波和自相关函数滤波处理后的图像如图2所示。

对模糊化的图像用逆滤波和约束最小二乘方滤波处理后的图像如图3所示。

由上述几幅图像可以看出,在没有噪声的情况下,三种复原方法的效果几乎是一样的。噪声为零时,维纳滤波,约束最小二乘方滤波可以认为就是逆滤波。
(2)选择一幅清晰的灰度图像,对该图像进行模糊化处理并加入高斯噪声,然后分别采用逆滤波、维纳滤波和约束最小二乘方滤波对退化图像进行复原。
原图像与加方差为0.001的噪声模糊图像如图4所示。

为模糊图像加方差为0.001的噪声时的四种滤波效果如下所示。其中维纳滤波的两种子方法,噪信功率比和自相关函数法滤波效果如图5所示。

加方差为0.001的噪声时逆滤波和约束最小二乘方法的滤波效果如图6所示。

原图像与加方差为0.008的噪声模糊图像如图7所示。

为模糊图像加方差为0.008的噪声时的四种滤波效果如下所示。其中维纳滤波的两种子方法,噪信功率比和自相关函数法滤波效果如图8所示。

加方差为0.008的噪声时逆滤波和约束最小二乘方法的滤波效果如图6所示。

由上文添加两种不同强度的噪声的滤波效果,比较复原结果可以看出,在有噪声时采用逆滤波进行复原效果很不好,在已知信噪比的情况的维纳滤波复原效果较次之,已知噪声和原图像的自相关函数的情况下的维纳滤波复原效果最佳。而对于高噪声,约束最小二乘方滤波要更好一些。
5. 典型的图像复原方法及其适用范围
- 逆滤波:适用于无噪声图像,一般对于有噪声的图像来说,直接逆滤波的性能是较差的。
- 最小均方差滤波(维纳)滤波:该方法建立在图像和噪声都是随机变量的基础上。未退化图像和噪声的功率谱必须是已知的。在没有噪声的情况下,维纳滤波可以看作是逆滤波。
- 约束最小二乘方滤波:仅仅用噪声的均值和方差的知识,就可以实现的最佳复原算法。但要假设噪声和图像灰度值不相关。
- 几何均值滤波:对维纳滤波的推广。
- 投影重建图像,卡尔曼滤波等。图像复原算法有线性和非线性两类。线性算法通过对图像进行逆滤波来实现反卷积。非线性方法通过连续的迭代过程不断提高复原质量,直到满足预先设定的终止条件,结果往往令人满意。
6. MATLAB程序代码
感兴趣的读者可获取参照下方方式获取实验代码和实验报告等资料。优先推荐途径一,若遇途径一失效,请再尝试途径二。
途径一
优先推荐该途径
第一步:扫描下方二维码,或打开微信搜索并关注“ 2贰进制 ”公众号;
第二步:回复“ MATLAB图像复原 ”即可获取本文相关资料。

途径二
优先推荐途径一,该途径管理可能不能秒回
扫描下方二维码,加入学习交流QQ群“ 480558240 ”,联系管理员获取包括但不限于本篇内容的更多学习资料。

2贰进制–Echo 2020年5月
我认同兴趣是最好的老师,但是除了兴趣其次是侮辱,所以如果您觉得本文还不错,请点赞+评论+收藏,要是关注那更是对我极大地羞辱了,您的羞辱便是我前进的动力!
如果本文对你有所帮助,解决了您的困扰,可以通过赞赏来给予我更大支持:

此致
感谢您的阅读、点赞、评论、收藏与打赏。