拉丁超立方的一些理解
- 基本原理:在一个设计空间中抽取n个样本,每一个样本点由m个分量组成。将每一个分量的取值范围均分为n个,将这n个样本随机地投放到设计空间中,在投放地的时候需要满足以下两个基条件。
- 拉丁超立方的两个基本要求:
(1)每一个样本点在小区间内随机地分布;
(2)将所有样本点投影到任意一维时,每一个小区间内有且仅有一个样本点。
例1:10个样本点,每一个样本点由2个分量构成,取值范围为[0,1];;
- 那么拉丁方抽样可以设计为如下公式:
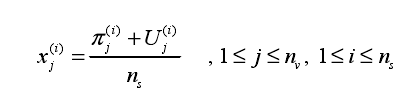
其中i代表第i个样本点;
j代表第i个样本点的第j个分量;
U j U_j Uj的取值为[0,1];
n s n_s ns为样本点总数;
π \pi π的取值为[0,n-1]的一个随机数。
根据前面的两个基本要求可以设计出以下matlab程序:
%% THIS project is an example for Latin hypercube sampling
clc
clear%%
number_dimension=2;
number_sample=10;sample=ones(number_sample,number_dimension);count1=0;
for i=1:1:number_dimensionpi_matrix=0:1:number_sample-1;for j=1:1:number_samplecount1=randsrc(1,1,pi_matrix);sample(j,i)=(count1+ unifrnd(0,1))/number_sample;index=find(pi_matrix==count1);pi_matrix(index)=[ ];endendscatter(sample(:,1),sample(:,2));
- 代码结果如下图;

例2:10个样本点,每一个样本点由7个分量构成,取值范围为[-10,10];
- 那么拉丁方抽样可以设计为如下公式:

x n o m a l i z e d 为 前 面 公 式 得 到 的 结 果 x_nomalized为前面公式得到的结果 xnomalized为前面公式得到的结果;
根据前面的两个基本要求可以设计出以下matlab程序:
%% THIS project is an example for Latin hypercube sampling
clc
clear%%
number_dimension=7;
number_sample=10;max_range_of_sample=10;
min_range_of_sample=-10;
distance=max_range_of_sample-min_range_of_sample;sample_pre=ones(number_sample,number_dimension);sample=ones(number_sample,number_dimension);count1=0;
for i=1:1:number_dimensionpi_matrix=0:1:number_sample-1;for j=1:1:number_samplecount1=randsrc(1,1,pi_matrix);sample_pre(j,i)=(count1+ unifrnd(0,1))/number_sample;index=find(pi_matrix==count1);pi_matrix(index)=[ ];sample(j,i)=distance*sample_pre(j,i)+min_range_of_sample;endendscatter(sample(:,1),sample(:,2));
- 代码结果如下图;

另参考:
归一化的两个常用方法



![[附源码]java毕业设计基于个性化的汽车购买推荐系统](https://img-blog.csdnimg.cn/ee7953222a0844c8b630d9b254ed0449.png)