一、坐标系变换

1. 世界坐标系与相机坐标系的变换关系

2. 相机坐标系与图像坐标系的变换关系

3. 图像坐标系与像素坐标系的变换关系

4. 从世界坐标系到像素坐标系的总体变换

二、参数标定

1. 封闭解

1.1 标定综合参数

1.2 标定内部参数

1.3 标定外部参数

1.4 径向畸变参数及校正

理论根据： 本文是基于张正友博士的论文理论而来，论文地址--提取码：ch6m。

一、坐标系变换

1. 世界坐标系与相机坐标系的变换关系

如图：

如图所示建立坐标系统，其中照相机坐标系 $Oxyz$ 的原点也是照相机的光心， $OO_{1}$ 为焦距 f(像距)。

从世界坐标系转换为相机坐标系的变换为：

$\begin{pmatrix} x\\ y\\ z \end{pmatrix}=R\begin{pmatrix} X_{w}\\ Y_{w}\\ Z_{w} \end{pmatrix}+T=\begin{pmatrix} r_{1} & r_{2} & r_{3} \\ r_{4} & r_{5} & r_{6} \\ r_{7} & r_{8} & r_{9} \end{pmatrix} * \begin{pmatrix} X_{w}\\ Y_{w}\\ Z_{w} \end{pmatrix} + \begin{pmatrix} t_{x}\\ t_{y}\\ t_{z} \end{pmatrix} (1)$

其中

$R=\begin{pmatrix} r_{1} & r_{2} & r_{3} \\ r_{4} & r_{5} & r_{6} \\ r_{7} & r_{8} & r_{9} \end{pmatrix}$

R为从世界坐标系到相机坐标系的旋转矩阵，

$T=\begin{pmatrix} t_{x}\\ t_{y}\\ t_{z} \end{pmatrix}$

T为世界坐标原点到相机坐标原点的平移矩阵

将(1)式写成齐次坐标形式：

$\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}=\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}=M\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}$

其逆变换为：

$\begin{pmatrix} X_{w}\\ Y_{w}\\ Z_{w} \end{pmatrix}=R^{-1}\begin{pmatrix} x\\ y\\ z \end{pmatrix}-R^{-1}\begin{pmatrix} t_{x}\\ t_{y}\\ t_{z} \end{pmatrix}(2)$

写为齐次形式：

$\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix} = \begin{bmatrix} R^{-1} & -R^{-1}T \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}$

2. 相机坐标系与图像坐标系的变换关系

考虑图中照相机坐标的任意一点P(x,y,z)，根据中心投影几何关系，有如下比例关系：

$\left\{\begin{matrix} X=fx/z\\ Y=fy/z \end{matrix}\right.$

写为齐次坐标形式：

$s\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}=\begin{bmatrix} f&0&0&0\\ 0&f&0&0\\ 0&0&1&0 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\1 \end{bmatrix}$

其中比例因子 $s=z$

逆变换关系为：

$\left\{\begin{matrix} x=zX/f\\ y=zY/f \end{matrix}\right.$

齐次坐标：

$\begin{bmatrix} x\\ y\\ z \end{bmatrix}=s\begin{bmatrix} f^{-1}&0&0\\ 0&f^{-1}&0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}$

3. 图像坐标系与像素坐标系的变换关系

如图：

zuobiao

假设相机像素坐标为 $\left ( u,v \right )$ ，单位是像素，照相机光轴与像面的交点坐标为 $\left ( u_{0},v_{0} \right )$ ，一般在像面中心附近。以 $\left ( u_{0},v_{0} \right )$ 为坐标原点 $O_{1}$ 建立新坐标系 $O_{1}XY$ ，并且设像素单位为 $dX$ 和 $dY$ ，则像素坐标系与图像坐标系之间的变换关系为：

$\left\{\begin{matrix} u=X/dX+u_{0}\\ v=Y/dY+v_{0} \end{matrix}\right.$

写作齐次坐标形式：

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} dX^{-1}&0&u_{0}\\0&dY^{-1}&v_{0} \\0&0&1 \end{bmatrix}\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}$

逆关系：

$\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}=\begin{bmatrix} dX&0&-u_{0}dX\\0&dY&-v_{0}dY \\0&0&1 \end{bmatrix}\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}$

4. 从世界坐标系到像素坐标系的总体变换

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=\begin{bmatrix} dX^{-1}&0&u_{0}\\0&dY^{-1}&v_{0} \\0&0&1 \end{bmatrix}\begin{bmatrix} X\\ Y\\ 1 \end{bmatrix}=\begin{bmatrix} dX^{-1}&0&u_{0}\\0&dY^{-1}&v_{0} \\0&0&1 \end{bmatrix}\begin{bmatrix} f&0&0&0\\0&f&0&0 \\0&0&1&0 \end{bmatrix}\begin{bmatrix} x\\ y\\z\\ 1 \end{bmatrix}$

$=\begin{bmatrix} dX^{-1}&0&u_{0}\\0&dY^{-1}&v_{0} \\0&0&1 \end{bmatrix}\begin{bmatrix} f&0&0&0\\0&f&0&0 \\0&0&1&0 \end{bmatrix}\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}$

$=\begin{bmatrix} dX^{-1}f&0&u_0&0\\0&dY^{-1}f&v_0&0 \\0&0&1&0 \end{bmatrix}\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}=\begin{bmatrix} \alpha _{x}&0&u_0&0\\0& \alpha_{y}&v_0&0 \\0&0&1&0 \end{bmatrix}\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}$

$=AM\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}$

其中， $\alpha_{x}=dX^{-1}f,\alpha_{y}=dY^{-1}f$ 为两个轴上的尺度因子（或者称为归一化焦距）。

且， $M=\begin{bmatrix} R & T \\ 0^{T} & 1 \end{bmatrix}$

为相机外部参数。

$A=\begin{bmatrix} \alpha _{x}&0&u_0&0\\0& \alpha_{y}&v_0&0 \\0&0&1&0 \end{bmatrix}$

为相机内部参数。

考虑到照相机的的不垂直度（描述两个坐标轴的倾斜角），照相机内部参数矩阵写作：

$A=\begin{bmatrix} \alpha _{x}&\gamma &u_0&0\\0& \alpha_{y}&v_0&0 \\0&0&1&0 \end{bmatrix}$

其中 $\gamma$ 为两个轴的不垂直度因子。

二、参数标定

1. 封闭解

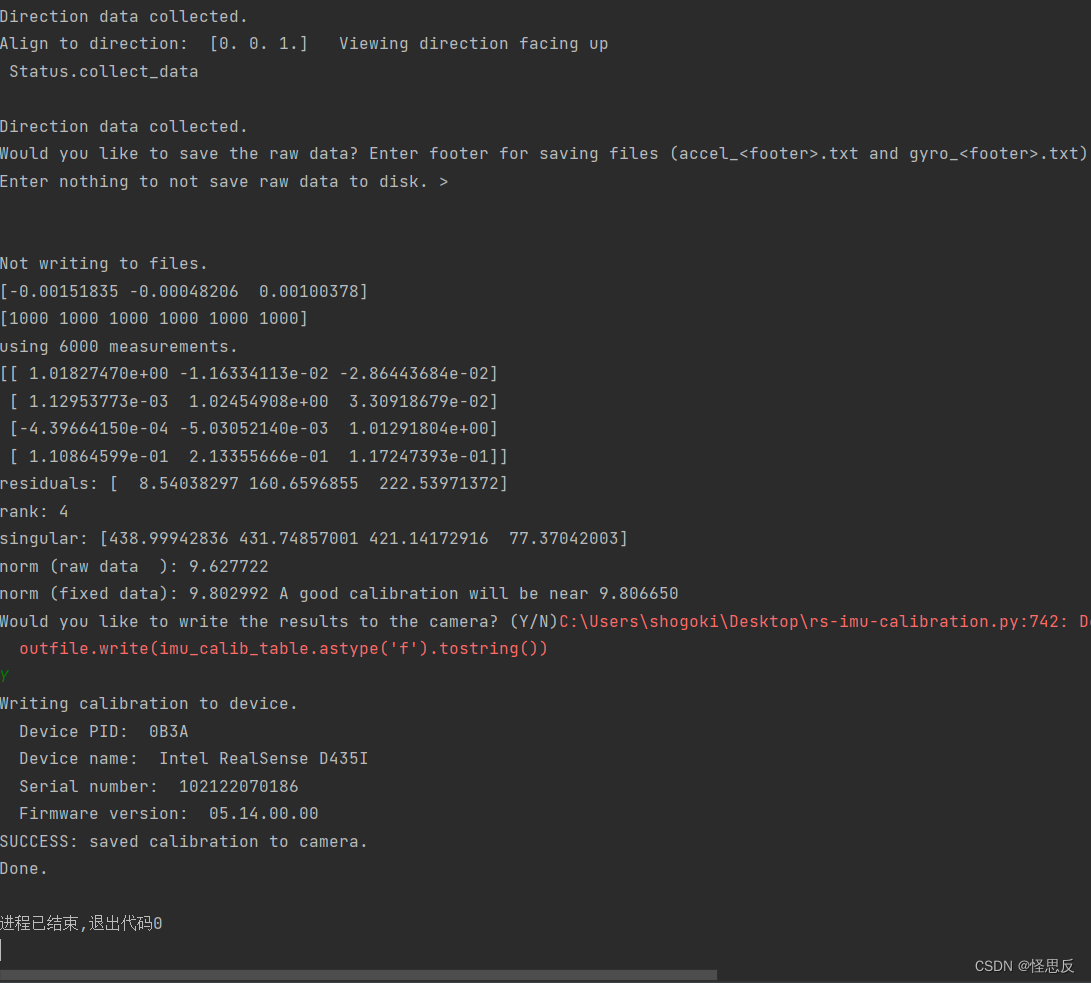
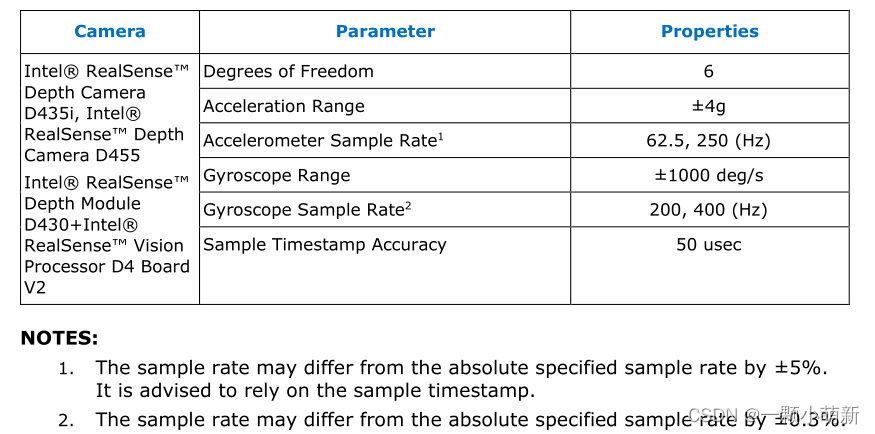
1.1 标定综合参数 $H$

由式：

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=AM\begin{bmatrix} X_{w}\\ Y_{w}\\ Z_{w}\\ 1 \end{bmatrix}$

对于两维标定模板，可以规定 $Z_{w}\equiv 0$ ，则

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=A\begin{bmatrix}r_{1}&r_{2}& r_{3}&T\end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ 0\\ 1 \end{bmatrix}$

简化为：

$s\begin{bmatrix} u\\ v\\ 1 \end{bmatrix}=A\begin{bmatrix}r_{1}&r_{2}& T\end{bmatrix}\begin{bmatrix} X_{w}\\ Y_{w}\\ 1 \end{bmatrix}$

假设

$H\equiv \begin{bmatrix} h_{1}& h_{2} &h_{3} \end{bmatrix}=\lambda A \begin{bmatrix} r_{1}& r_{2} & T \end{bmatrix}$

使得

$\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = H\begin{bmatrix} X_{w}\\ Y_{w}\\ 1 \end{bmatrix}$

注意这里的 $\lambda$ 与 $s$ 的关系。

使用最小二乘法计算 $H$ ，即使得根据上式计算得到图像坐标 $\tilde{m}$ 与实际图像坐标 $m$ 之间的残差最小，目标函数为：

$J=\sum_{i}^{n}\left \| m_{i} - \tilde{m_{i}}\right \|^{2}$

下面计算 $H$ 的初始化过程：

对于第i对对应点有

$\begin{bmatrix} u_{i}\\ v_{i}\\ 1 \end{bmatrix}= \begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33} \end{bmatrix}\begin{bmatrix} X_{i}\\ Y_{i}\\ 1 \end{bmatrix}$

两边叉乘 $\begin{bmatrix} u_{i}\\ v_{i}\\ 1 \end{bmatrix}$ 得到

$\begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33} \end{bmatrix}\begin{bmatrix} X_{i}\\ Y_{i}\\ 1 \end{bmatrix}\times \begin{bmatrix} u_{i}\\ v_{i}\\ 1 \end{bmatrix}= 0$

化为三个分量方程

$\left ( h_{12}X_{i}+h_{22}Y_{i}+h_{32} \right )-\left ( h_{13}X_{i}+h_{23}Y_{i}+h_{33} \right )v_{i}=0$

$\left ( h_{13}X_{i}+h_{23}Y_{i}+h_{33} \right )u_{i}-\left ( h_{11}X_{i}+h_{21}Y_{i}+h_{31} \right )=0$

$\left ( h_{11}X_{i}+h_{21}Y_{i}+h_{31} \right )v_{i}-\left ( h_{12}X_{i}+h_{22}Y_{i}+h_{32} \right )u_{i}=0$

这是一个关于9个未知数 $\begin{bmatrix} h_{11} & h_{21} & h_{31} & h_{12} & h_{22} & h_{32} & h_{13} & h_{23} & h_{33} \end{bmatrix}^{T}$ 的齐次方程组，

系数矩阵为

$\begin{bmatrix} 0 & 0 & 0 & X_{i} & Y_{i} & 1 & -X_{i}v_{i} & -Y{i}v_{i} & -v_{i}\\ -X_{i} & -Y_{i} & -1 & 0 & 0 & 0 & X_{i}u_{i} & Y_{i}u_{i} & u_{i}\\ X_{i}v_{i} & Y_{i}v_{i} & v_{i} & -X_{i}u_{i} & -Y_{i}u_{i} & -u_{i} & 0 & 0 & 0 \end{bmatrix}$

对于 $n$ 个点对，可以得到 $3n\times 9$ 的系数矩阵，该系数矩阵可以通过奇异值分解得到 $H$ 。

1.2 标定内部参数

由

$H\equiv \begin{bmatrix} h_{1} & h_{2} & h_{3} \end{bmatrix}=\lambda A\begin{bmatrix} r_{1} & r_{2} & T \end{bmatrix}$

且 $r_{1}\cdot r_{2}=0$ 和 $r_{1}^{2}=r_{2}^{2}=1$ 可得

$h_{1}^{T}A^{-T}A^{-1}h_{2}=0$

$h_{1}^{T}A^{-T}A^{-1}h_{1}=h_{2}^{T}A^{-T}A^{-1}h_{2}$

设

$B= A^{-T}A^{-1}=\begin{bmatrix} B_{11} & B_{12} & B_{13}\\ B_{21} & B_{22} & B_{23}\\ B_{31} & B_{32} & B_{33} \end{bmatrix}$

将两个方程写成分量形式

$h_{11}H_{21}B_{11}+(h_{11}h_{22}+h_{12}h_{21})B_{12}+(h_{11}h_{23}+h_{21}h_{13})B_{13}+h_{12}h_{22}B_{22}+(h_{13}h_{22}+h_{12}h_{23})B_{23}+h_{13}h_{23}B_{33}=0$

$(h_{11}^{2}-h_{21}^{2})B_{11}+(h_{12}^{2}-h_{22}^{2})B_{22}+(h_{13}^{2}-h_{23}^{2})B_{33}+2(h_{11}h_{12}-h_{21}h_{22})B_{12}+2(h_{11}h_{13}-h_{21}h_{23})B_{13}+2(h_{12}h_{13}-h_{22}h_{23})B_{23}=0$

将方程合并

$\begin{bmatrix} h_{11}h_{21} & h_{11}h_{22}+h_{12}h_{21} & h_{12}h_{22} & h_{11}h_{23}+h_{21}h_{13} & h_{13}h_{22}+h_{12}h_{23} & h_{13}h_{23}\\ h_{11}^{2}-h_{21}^{2} & 2(h_{11}h_{12}-h_{21}h_{22}) & h_{12}^{2}-h_{22}^{2} & 2(h_{11}h_{13}-h_{21}h_{23}) & 2(h_{12}h_{13}-h_{21}h_{23}) & h_{13}^{2}-h_{23}^{2} \end{bmatrix}\begin{bmatrix} B_{11}\\ B_{12}\\ B_{22}\\ B_{13}\\ B_{23}\\ B_{33} \end{bmatrix}=0$

进一步解得内部参数为

$v_{0}=\frac{B_{12}b_{13}-B_{11}B_{23}}{B_{11}B_{22}-B_{12}^{2}}$

$\tau =B_{33}-\frac{B_{13}^{2}+v_{0}(B_{12}B_{13}-B_{11}B_{23})}{B_{11}}$

$\alpha =\sqrt{\frac{\tau }{B_{11}}}$

$\beta =\sqrt{\frac{\tau B_{11}}{B_{11}B_{22}-B_{12}^2}}$

$\gamma =-\frac{B_{12}\alpha ^{2}\beta }{\tau }$

$u_{0}=\frac{\gamma v_{0}}{\alpha }-\frac{B_{13}\alpha ^{2}}{\tau }$

1.3 标定外部参数

进一步解得外部参数为

$r_{1}=sA^{-1}h_{1}$

$r_{2}=sA^{-1}h_{2}$

$r_{3}=r_{1}\times r_{2}$

$T=sA^{-1}h_{3}$

注意这里的

$s=\frac{1}{\left \| A^{-1}h_{1} \right \|}=\frac{1}{\left \| A^{-1}h_{2} \right \|}$

注意这里 $\lambda$ 与 $s$ 的关系。

转换为

$R=(r_{1} r_{2} r_{3})$

1.4 径向畸变参数及校正

由

$\begin{pmatrix} x\\ y\\ T \end{pmatrix}=\begin{pmatrix} r_{1} & r_{2} & T \end{pmatrix}\begin{pmatrix} X_{w}\\ Y_{w}\\ 1 \end{pmatrix}$

$\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{s}A\begin{pmatrix} x\\ y\\ T \end{pmatrix}$

由

$\left\{\begin{matrix} \check{x}=x+x[k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}]\\ \check{y}=y+y[k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}]\end{matrix}\right.$

从而

$\left\{\begin{matrix} \check{u}=u+(u+u_{0})[k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}]\\ \check{v}=v+(v+v_{0})[k_{1}(x^{2}+y^{2})+k_{2}(x^{2}+y^{2})^{2}]\end{matrix}\right.$

建立如下方程组

$\begin{bmatrix} (u-u_{0})(x^{2}+y^{2}) & (u-u_{0}(x^{2}+y^{2})^{2})\\ (v-v_{0})(x^{2}+y^{2}) & (v-v_{0}(x^{2}+y^{2})^{2}) \end{bmatrix}\begin{bmatrix} k_{1}\\ k_{2} \end{bmatrix}=\begin{bmatrix} \check{u}-u\\ \check{v}-v \end{bmatrix}$