数据分析：麦当劳食品营养数据探索并可视化

news/2024/12/31 1:59:00/

在这里插入图片描述

系列文章目录

作者：i阿极

作者简介：Python领域新星作者、多项比赛获奖者：博主个人首页

😊😊😊如果觉得文章不错或能帮助到你学习，可以点赞👍收藏📁评论📒+关注哦！👍👍👍

📜📜📜如果有小伙伴需要数据集和学习交流，文章下方有交流学习区！一起学习进步！💪

专栏案例：数据分析
数据分析：某电商优惠卷数据分析
数据分析：旅游景点销售门票和消费情况分析
数据分析：消费者数据分析
数据分析：餐厅订单数据分析
数据分析：基于随机森林(RFC)对酒店预订分析预测
数据分析：基于K-近邻(KNN)对Pima人糖尿病预测分析

文章目录

  • 系列文章目录
  • 1、实验简介
  • 2、数据说明
    • 2.1数据集的整体特征
    • 2.2属性描述
  • 3、实验环境
  • 4、实验步骤
    • 4.1数据准备
    • 4.2数据质量检查
    • 4.3探索性分析
    • 4.4通过轮廓图和相关图来比较特征

1、实验简介

麦当劳（McDonald’s）是源自美国南加州的跨国连锁快餐店，也是全球最大的快餐连锁店，主要贩售汉堡包及薯条、炸鸡、汽水、冰品、沙拉、水果、咖啡等快餐食品。近年来，越来越多的人意识到快餐食品的不健康性，麦当劳也成了“垃圾食品”的代名词。美国纪录片《Super Size Me》记录了一个人一个月内只吃麦当劳后的身体变化，更引起了人们对于快餐食品营养超标的担忧。本分析旨在通过实证方法评估麦当劳数据集中260个产品的营养成分，我们先从一些标准的数据探索分析开始，之后讨论并使用Plotly绘制交互式散点图以展示不同的营养指标。

2、数据说明

2.1数据集的整体特征

|数据集名称 |数据类型 |特征数 |实例数 |值缺失 |相关任务|

数据集名称数据类型特征数实例数值缺失相关任务
麦当劳餐品营养成分数据集字符、数值数据242600可视化

2.2属性描述

属性数据类型字段描述
CategoryString食物类别
ItemString食品名称
Serving SizeString食用分量
CaloriesInteger卡路里
Calories from FatInteger来自脂肪的卡路里
Total FatInteger脂肪总量
Total Fat (% Daily Value)Integer脂肪总量占每日推荐摄入量的百分比
Saturated FatInteger饱和脂肪
Saturated Fat (% Daily Value)Integer饱和脂肪占每日推荐摄入量的百分比
Trans FatInteger反式脂肪
CholesterolInteger胆固醇
Cholesterol (% Daily Value)Integer胆固醇占每日推荐摄入量的百分比
SodiumInteger钠
Sodium (% Daily Value)Integer钠占每日推荐摄入量的百分比
CarbohydratesInteger碳水化合物
Carbohydrates (% Daily Value)Integer碳水化合物占每日推荐摄入量的百分比
Dietary FiberInteger膳食纤维
Dietary Fiber (% Daily Value)Integer膳食纤维占每日推荐摄入量的百分比
SugarsInteger糖分
ProteinInteger蛋白质
Vitamin A (% Daily Value)Integer维他命A占每日推荐摄入量的百分比
Vitamin C (% Daily Value)Integer维他命C占每日推荐摄入量的百分比
Calcium (% Daily Value)Integer钙占每日推荐摄入量的百分比
Iron (% Daily Value)Integer铁占每日推荐摄入量的百分比

3、实验环境

Python 3.9

Anaconda

Jupyter Notebook

4、实验步骤

4.1数据准备

加载需要的模块

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import warnings
warnings.filterwarnings('ignore')

加载数据


#加载数据集
menu = pd.read_csv("/home/mw/mcdonald_s_menu.csv")#预览数据集前5行
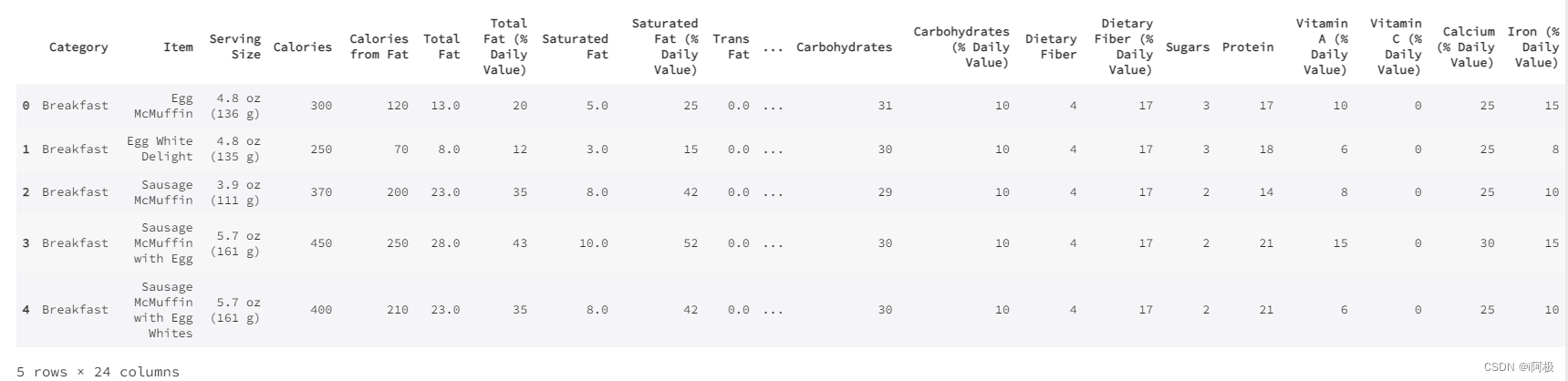
menu.head()

在这里插入图片描述

查看数据集行列数

print("该数据集共有 {} 行 {} 列".format(menu.shape[0],menu.shape[1]))

在这里插入图片描述

每一行代表一样麦当劳产品；24列，包括了产品的类别，名称，大小，以及营养成分（如卡路里，脂肪，胆固醇，钠，碳水化合物，膳食纤维，糖，蛋白质，维他命A，维他命C，钙，铁）等内容。

4.2数据质量检查

检查空值

menu.isnull().any()

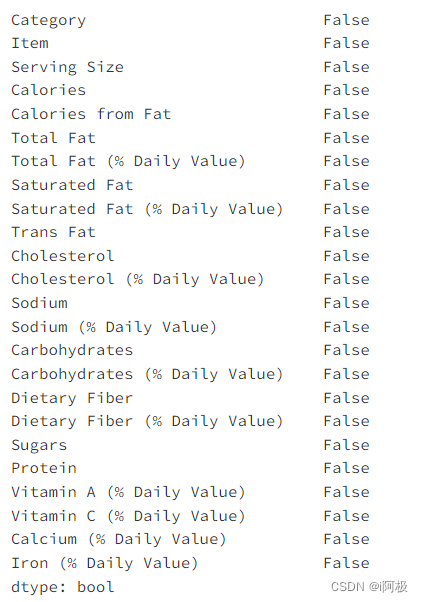
在这里插入图片描述

各个column内容的描述性统计

menu.describe()

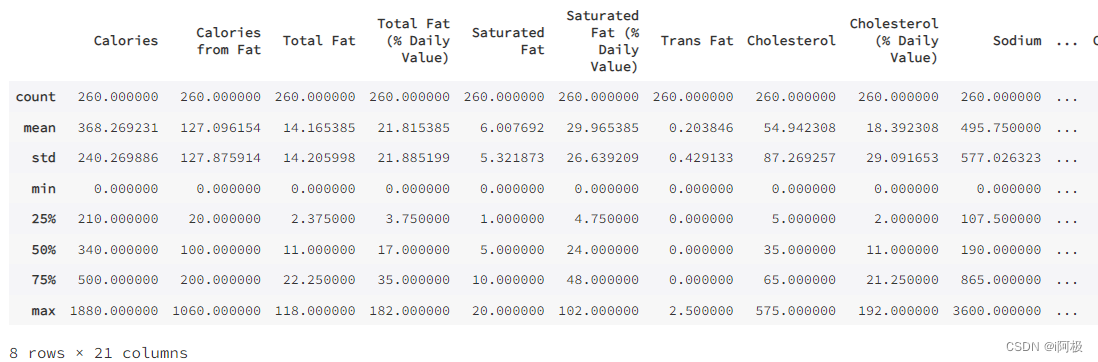
在这里插入图片描述

4.3探索性分析

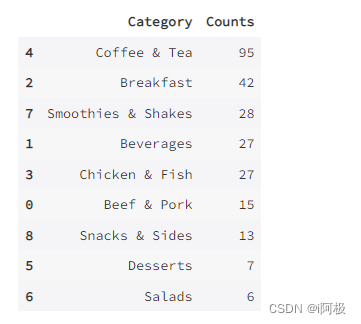
首先，我们看一下每一类食品的数量，并绘图展示：

count_by_category = menu[["Category"]].groupby(["Category"]).size().reset_index(name = 'Counts').sort_values(by = "Counts", ascending = False)
count_by_category

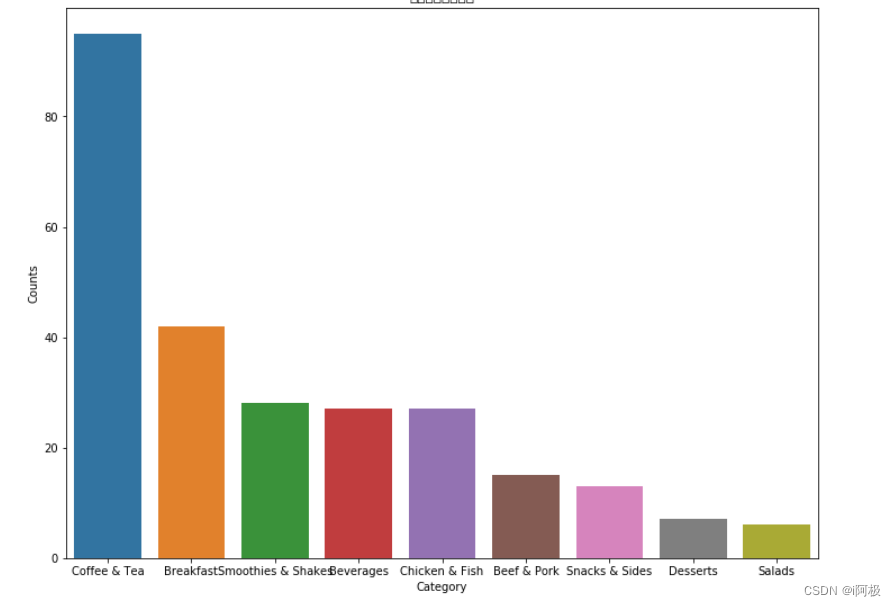
在这里插入图片描述

#条形图
fig, ax = plt.subplots(figsize = (12,9))
ax = sns.barplot(x="Category", y="Counts", data = count_by_category).set_title("每一类食品的数量")

在这里插入图片描述

#饼形图
plt.figure(figsize = (12,9))
plt.pie(x = count_by_category["Counts"], labels=count_by_category["Category"], autopct='%1.0f%%',)
plt.show()

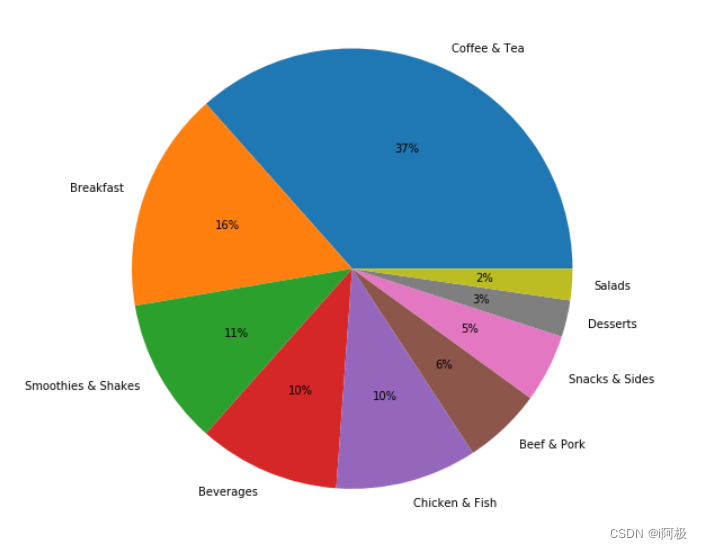
在这里插入图片描述

从条形图和饼形图可以看出，数量排名第一的品类是咖啡和茶，高达37%；之后是早餐（16%），冰沙奶昔（11%），饮品（10%），鸡肉鱼肉（10%）和牛肉猪肉（6%）。小吃，甜点和沙拉占比最少，其中沙拉类食品仅占所有食品的2%。

接下来，我们看看，不同品类的食物，其卡路里含量如何

#盒形图
fig, ax = plt.subplots(figsize = (12,9))
ax = sns.boxplot(x = 'Category', y = 'Calories', data = menu).set_title("卡路里")

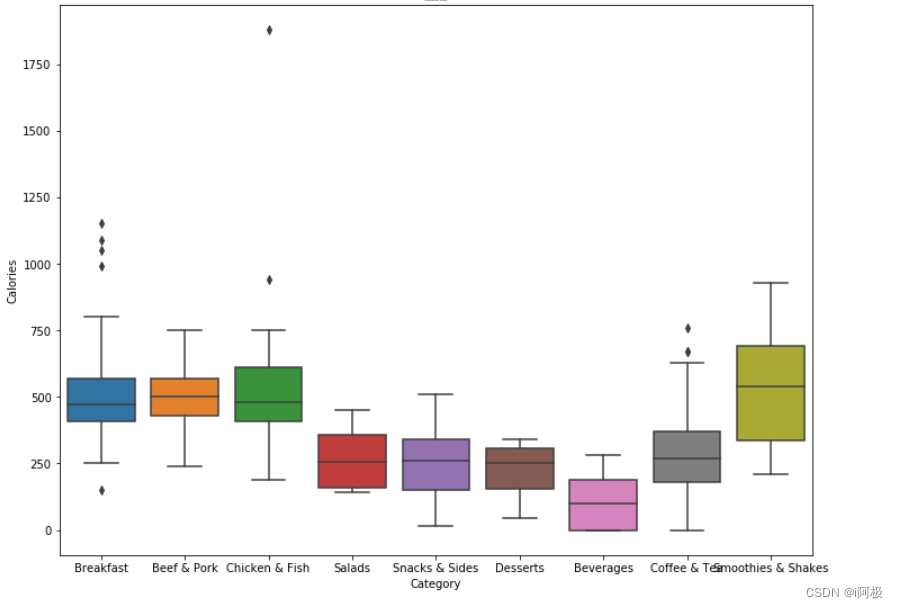
在这里插入图片描述

一些有趣的发现：

  • 早餐系列、猪肉牛肉系列、鸡肉鱼肉系列的卡路里含量较高（主食），冰沙奶昔系列的卡路里含量最高；
  • 沙拉、小食、甜品、咖啡和茶的卡路里含量较低，饮品的卡路里含量最低；
  • 早餐系列、鸡肉鱼肉系列和咖啡茶系列有一些异常值(outlier)，可能是一些大份食物。

以上分析提醒了我们，食品的卡路里含量（及其他成分含量）会受到其份量的影响，将食品调整至同样的份量可以让之后的分析更加客观。

通过回顾数据集中“Serving Size”一栏，我们发现麦当劳对份量的标注并不完全统一，有如下几种形式：

1）4.8 oz (136 g) 2）1 cookie (33 g) 3）21 fl oz cup 4) 1 carton (236 ml) 5) 6 fl oz (177 ml) 6) 16.9 fl oz

固体食物的份量标注比较统一，都是按1）的形式，标出了oz和g两种重量单位，唯一的特例是2），只标注了g这一重量单位。

半液态和液态食物的份量标注比较杂乱，有些和固体食物一样标注了重量，但大部分属于3）-6），即标注fl oz和/或ml两种体积单位。

因此我们的提取原则是，重量单位优先提取g，没有g再提取oz，并转换为g；体积单位优先提取ml，没有ml再提取fl oz，并转换为ml。

*注：1盎司(oz)=28.35克(g)；1美制液体盎司(fl oz)=29.57毫升(ml)

因为重量单位和体积单位的不一致，为了之后的分析方便，我们假设1ml的液体等于1g，并把一些半液态和液态食品的份量从体积转为重量。

将食品调整至同样的份量(按100g计算)

#正则表达式匹配几种不同的份量标注方式
import re
p1 = re.compile(r'[(](.*?)[ g)]')
p2 = re.compile(r'(.*?)[ ]')#定义函数，提取份量数据
def getLambda(x, p1, p2):try: val = float(re.findall(p1,x)[0])except:val = float(re.findall(p2,x)[0]) * 29.57 # 提取的是fl oz，乘以29.57转换为mlreturn val#调整menu数据集
norm_menu = menu.iloc[:,:]
norm_menu["Size g"] = norm_menu["Serving Size"].apply(lambda x: getLambda(x, p1, p2))
norm_menu["Calories per 100g"] = (norm_menu['Calories']/norm_menu["Size g"]) * 100norm_menu.head()

#盒形图
fig, ax = plt.subplots(figsize = (12,9))
sns.boxplot(x = 'Category', y = 'Calories per 100g', data = norm_menu)

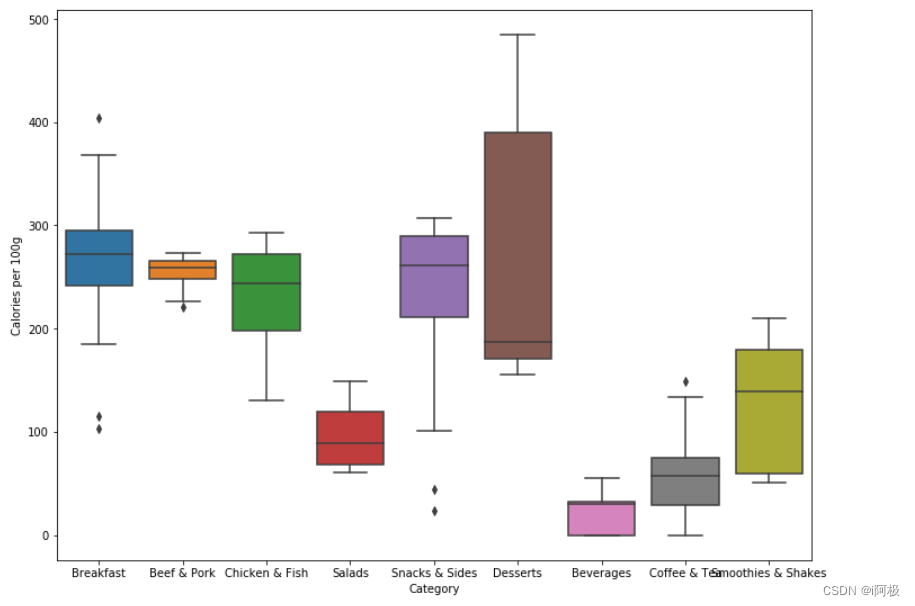
在这里插入图片描述

对比没有调整过的数据画出的盒形图可以得知：

  • 固态食品中，主食（早餐，牛肉猪肉，鸡肉鱼肉）依旧是卡路里含量最高的食品。之前我们以为卡路里含量较低的小食、甜点等，其实只是因为份量较小，如果换算成同样的份量，卡路里含量也不低，和主食持平。只有沙拉的卡路里含量远低于其他类食品，其平均值是主食的一半左右。
  • 液体及半液体的饮品，卡路里含量总体低于固体食品，但冰沙奶昔的卡路里明显高于饮料和咖啡茶，甚至高于沙拉。

因此，对于一个选择麦当劳就餐的减肥人士来说，为了填饱肚子，最好点一份沙拉。如果还想点一份饮品，不建议点冰沙奶昔。

4.4通过轮廓图和相关图来比较特征

轮廓图

我们首先看看一个特征如何影响其他特征：轮廓图或者KDE图可以提供一个特征相对于另一个特征的分布。简单来讲，这让我们对定量数据有一个快速的感知。调用了Seaborn中的kdeplot函数。我们选取了几个主要特征，并生成了9张轮廓图，如下所示：

# KDE图
f, axes = plt.subplots(3, 3, figsize=(10, 10), sharex=True, sharey=True)s = np.linspace(0, 3, 10)
cmap = sns.cubehelix_palette(start=0.0, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Cholesterol (% Daily Value)'].values
y = menu['Sodium (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, cut=5, ax=axes[0,0])
axes[0,0].set(xlim=(-10, 50), ylim=(-30, 70), title = 'Cholesterol and Sodium')cmap = sns.cubehelix_palette(start=0.333333333333, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Carbohydrates (% Daily Value)'].values
y = menu['Sodium (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[0,1])
axes[0,1].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Carbs and Sodium')cmap = sns.cubehelix_palette(start=0.666666666667, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Carbohydrates (% Daily Value)'].values
y = menu['Cholesterol (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[0,2])
axes[0,2].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Carbs and Cholesterol')cmap = sns.cubehelix_palette(start=1.0, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Total Fat (% Daily Value)'].values
y = menu['Saturated Fat (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[1,0])
axes[1,0].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Total Fat and Saturated Fat')cmap = sns.cubehelix_palette(start=1.333333333333, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Total Fat (% Daily Value)'].values
y = menu['Cholesterol (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[1,1])
axes[1,1].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Cholesterol and Total Fat')cmap = sns.cubehelix_palette(start=1.666666666667, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Vitamin A (% Daily Value)'].values
y = menu['Cholesterol (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[1,2])
axes[1,2].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Vitamin A and Cholesterol')cmap = sns.cubehelix_palette(start=2.0, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Calcium (% Daily Value)'].values
y = menu['Sodium (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[2,0])
axes[2,0].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Calcium and Sodium')cmap = sns.cubehelix_palette(start=2.333333333333, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Calcium (% Daily Value)'].values
y = menu['Cholesterol (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[2,1])
axes[2,1].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Cholesterol and Calcium')cmap = sns.cubehelix_palette(start=2.666666666667, light=1, as_cmap=True)# Generate and plot a random bivariate dataset
x = menu['Iron (% Daily Value)'].values
y = menu['Total Fat (% Daily Value)'].values
sns.kdeplot(x, y, cmap=cmap, shade=True, ax=axes[2,2])
axes[2,2].set(xlim=(-5, 50), ylim=(-10, 70),  title = 'Iron and Total Fat')f.tight_layout()

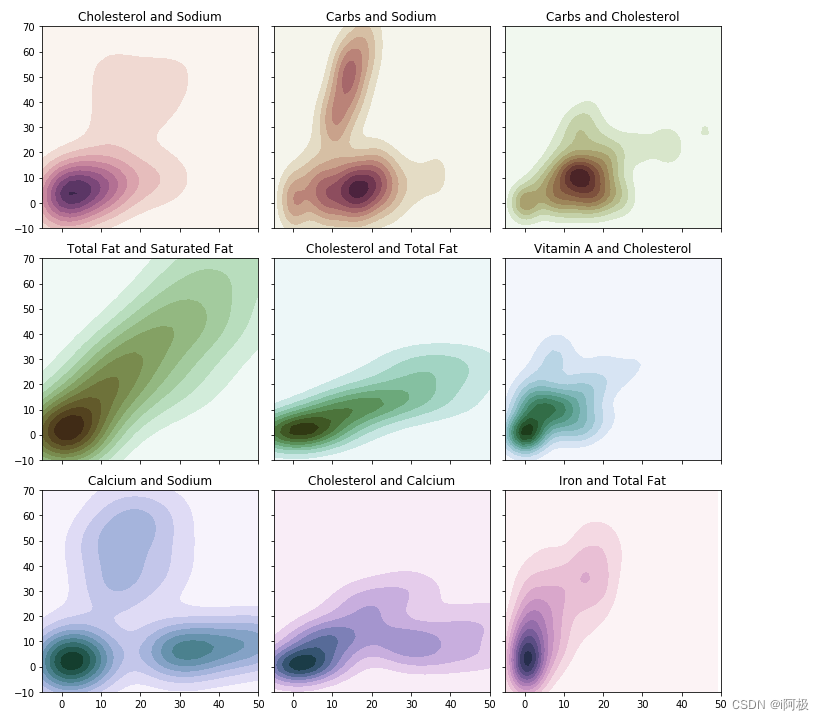
在这里插入图片描述

Pearson相关图

现在绘制Pearson相关图，检查不同营养指标之间的相关程度。这次，我们调用了Plotly的交互式绘图功能，绘制特征之间相关性的热图（Heatmap），如下所示：

data = [go.Heatmap(z = menu.iloc[:, 3:].corr().values,x = menu.columns.values,y = menu.columns.values,colorscale = 'Viridis',text = menu.iloc[:, 3:].corr().round(2).astype(str),opacity = 1.0)
]layout = go.Layout(title = '各个营养指标的Pearson相关图',xaxis = dict(ticks='', nticks=36),yaxis = dict(ticks=''),width = 900, height = 700,
)fig = go.Figure(data = data, layout = layout)
py.iplot(fig, filename = 'labelled-heatmap')

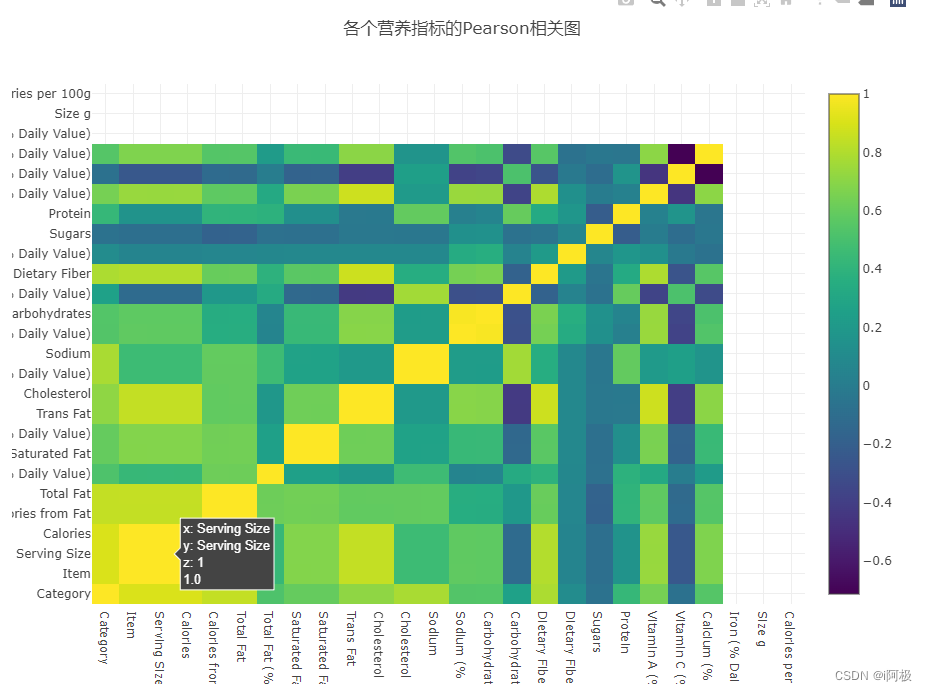
在这里插入图片描述

点击不同的方格，可以查看某两个特征的相关性。颜色越趋近于黄色，说明两者正相关性越强。颜色越趋近于紫色，说明两者负相关性越强。

  • 从相关图中可以看出明显相关的特征，例如份量和卡路里的相关性高达0.9。
  • 然而，有一些相关性非常不直观。例如，总脂肪和饱和脂肪/反式脂肪之间存在相当弱的相关性，但在我们普通人的认知中，这两者理应早存一定相关性。
  • 热图也从负相关图（深蓝/黑）的斑点中引出了有趣的发现。例如，它表明碳水化合物通常与反式脂肪，胆固醇，钠，膳食纤维和维生素A呈负相关。这与碳水化合物的负相关性确实很多。

数据质量是否存在任何问题？

  • 现在很明显，碳水化合物列与其他列负相关程度很强，这是符合常识的。然而，或许存在如下可能性：含碳水化合物的食物可能除了碳水化合物之外没有其他东西，从而导致了上面提到的负相关性，这也是需要在分析中结合实际情况思考的。

订阅热门专栏：
《数据分析之道》
《数据分析之术》
《机器学习案例》
《数据分析案例》

📢文章下方有交流学习区！一起学习进步！💪💪💪
📢首发CSDN博客，创作不易，如果觉得文章不错，可以点赞👍收藏📁评论📒
📢你的支持和鼓励是我创作的动力❗❗❗


http://www.ppmy.cn/news/48351.html

相关文章

安全防御 --- 防火墙高可靠技术

安全防御 --- 防火墙高可靠技术

防火墙高可靠技术（双机热备） VRRP：负责的单个接口的故障检测和流量引导。每个VRRP备份组拥有一个虚拟的IP地址，作为网络的网关地址；在VRRP主备倒换时通过发送免费的ARP来刷新对接设备的MAC地址转发表来引导流量。VGMP&…
阅读更多...
阿里，字节，拼多多，B站挨个面试一遍，你们猜哪个待遇最高？

阿里，字节，拼多多，B站挨个面试一遍，你们猜哪个待遇最高？

我面试的是软件测试岗位，去年中旬的时候从原来的公司离职了，不是工作不好，而是公司发展速度太慢，自己干了几年，也没有太大的成长。以我目前的工作经验和实力，我认为准备一两个月，进大厂不是什么…
阅读更多...
手把手教你实现el-table实现跨表格禁用选项，以及禁用选择后，对应的全选按钮也要禁用任何操作

手把手教你实现el-table实现跨表格禁用选项，以及禁用选择后，对应的全选按钮也要禁用任何操作

哈喽 大家好啊 今天我要实现不能跨表格选择，如果我选择了其中一个表格的选项后，那么其他的表格选项则被禁用 然后我选择了其中一个表格行，我其他的表格选项则应该被禁用 实现代码： 其中关键属性： selectable仅对 typ…
阅读更多...
【越早知道越好】的道理——能够大大提升效率的【快捷键】

【越早知道越好】的道理——能够大大提升效率的【快捷键】

文章目录 1️⃣虚拟桌面⚜️第一步：打开任务视图⚜️第二步：创建桌面⚜️第三步：桌面切换⚜️第四步：桌面删除 2️⃣窗口切换3️⃣桌面分屏⚜️如何分屏 前言🧑‍🎤：作为程序员👨‍&…
阅读更多...
Linux基础内容（20）—— 共享内存

Linux基础内容（20）—— 共享内存

Linux基础内容（19）—— 进程间通信(介绍与管道内容)_哈里沃克的博客-CSDN博客https://blog.csdn.net/m0_63488627/article/details/130034918?spm1001.2014.3001.5502 目录 1.共享内存的原理 2.共享内存的概念和特点 创建共享内存 共享内存的形式…
阅读更多...
第七章节 spring AOP

第七章节 spring AOP

《Spring》篇章整体栏目 ————————————————————————————— 【第一章】spring 概念与体系结构 【第二章】spring IoC 的工作原理 【第三章】spring IOC与Bean环境搭建与应用 【第四章】spring bean定义 【第五章】Spring 集合注入、作用域 【第六章】…
阅读更多...
什么是计算量flops，什么是参数量params？

什么是计算量flops，什么是参数量params？

flops与params 计算量对应我们之前的时间复杂度，参数量对应于我们之前的空间复杂度，这么说就很明显了 也就是计算量要看网络执行时间的长短，参数量要看占用显存的量 其中最重要的衡量CNN 模型所需的计算力就是flops： FLOPS&…
阅读更多...
显存不够用？一种大模型加载时节约一半显存的方法

显存不够用？一种大模型加载时节约一半显存的方法

Loading huge PyTorch models with linear memory consumption 本文主要介绍了一种用于加载巨大模型权重时节约接近一半显存的方法 首先，创建一个模型: import torch from torch import nnclass BoringModel(nn.Sequential):def __init__(self):super().__init__…
阅读更多...
最新文章

Copyright @ 2022~2023