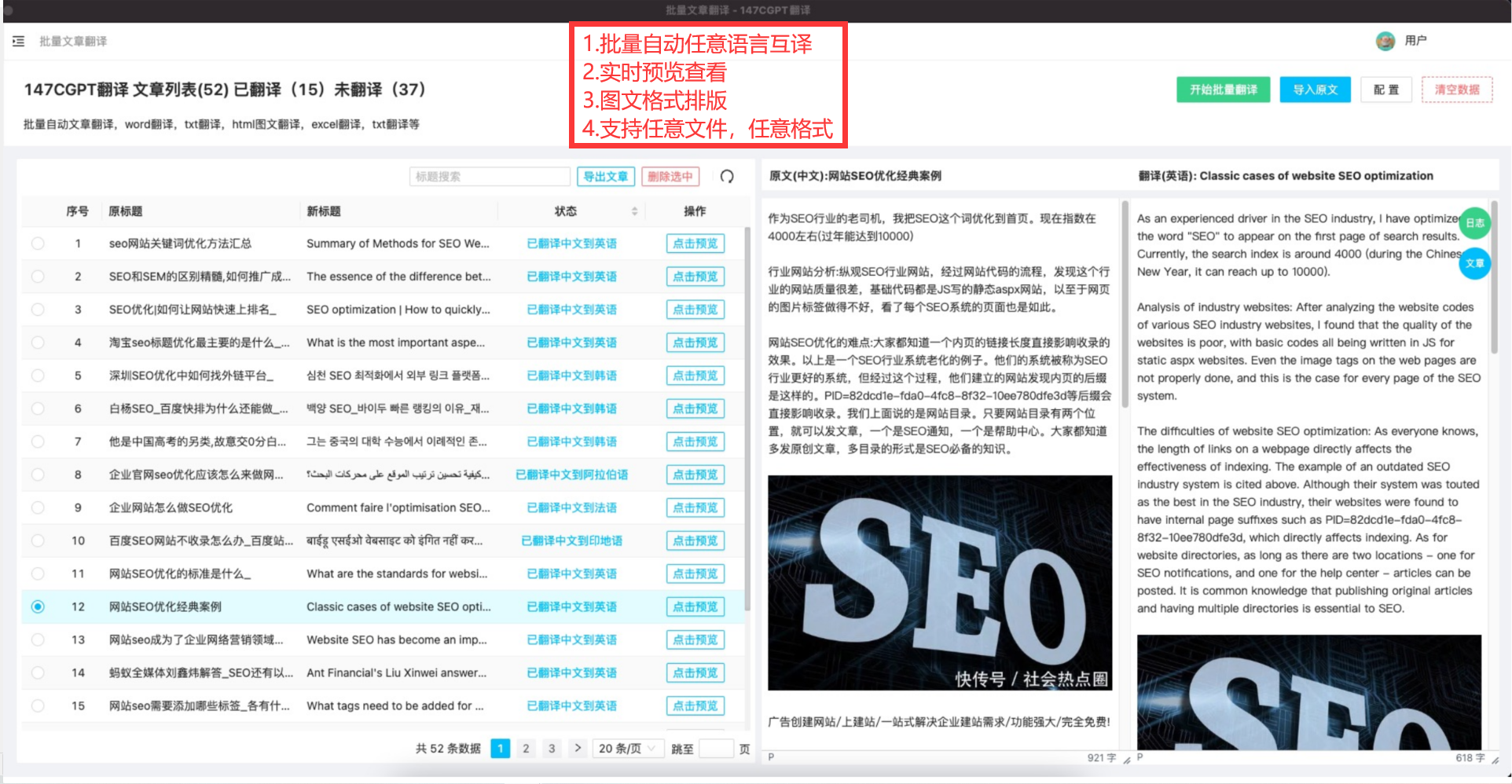
目录
1.三次Hermite曲线的参数方程
2. 三次Hermite曲线的绘制
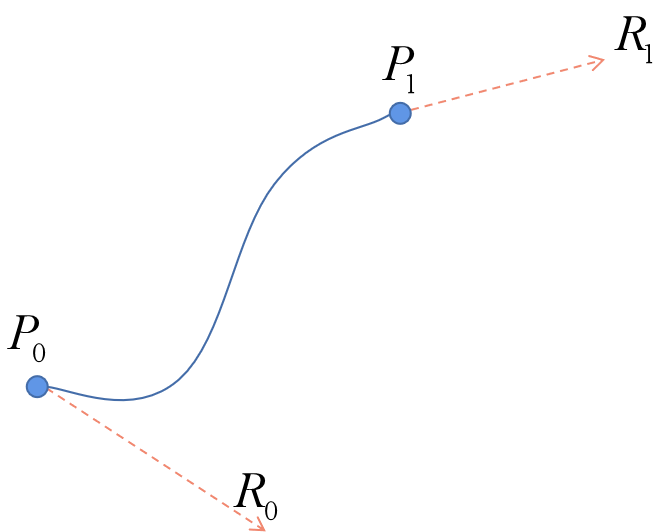
Hermite曲线是通过给定曲线的两个端点的位置矢量、
以及两个端点处的切线矢量
、
来描述曲线的,如图1所示。这里先对Hermite曲线进行数学公式推导,然后讲述如何绘制Hermite曲线。(这里是算法代码)
1.三次Hermite曲线的参数方程
三维空间中的自由曲线用三次参数方程表示可以用以下的形式:
或者:
其中,参数t的取值范围是,这是归一化坐标,表示从端点1到端点2的的相对距离。
将以上参数方程改写为矩阵形式为:
若令
则
对参数t的一阶导数得:
假定已知曲线的两个端点的位置矢量、
以及两个端点处的切线矢量
、
,如图1所示。注意位置矢量和切线矢量都有x,y等分量。这四个量实际上对应于将t=0好t=1代入
、
得到的结果,即:
用矩阵方程表示为:
则
令
即为Hermite矩阵,为常数,
为Hermite几何矢量。
则
于是曲线又可以表示为:
因为上面的和
都是三维空间的矢量,有x,y,z三个分量:
于是将曲线Q展开成分量形式如下:
显然,只要给定,就可以在
的范围内求出
,形成曲线上点的轨迹。
称之为Hermite基函数。对基函数进行进一步展开,得到四个分量:
于是曲线上的轨迹点,又可以通过以下公式表示:
2. 三次Hermite曲线的绘制
这里是代码下载链接:Hermite曲线绘制代码
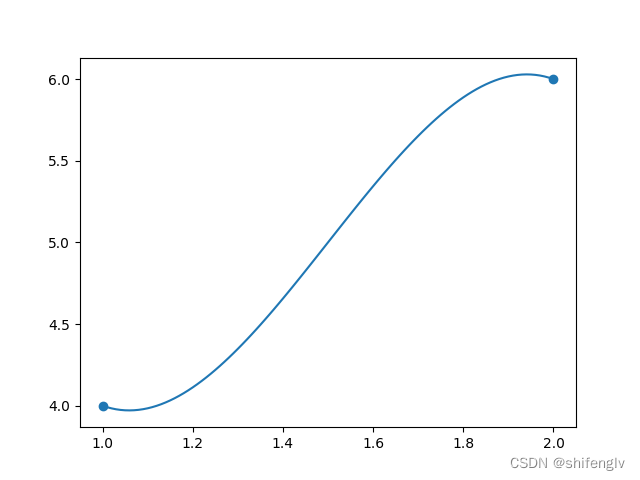
三次Hermite曲线的绘制,需要四个参数进行控制,分别是两个端点坐标和两个端点处的切线矢量,比如给定两个点的三维坐标P0(1,4,0)、P1(2,6,0),以及两个端点的切线矢量R0(1,-1,0)、R1(1,-1,0),其绘制的Hermite曲线如下:
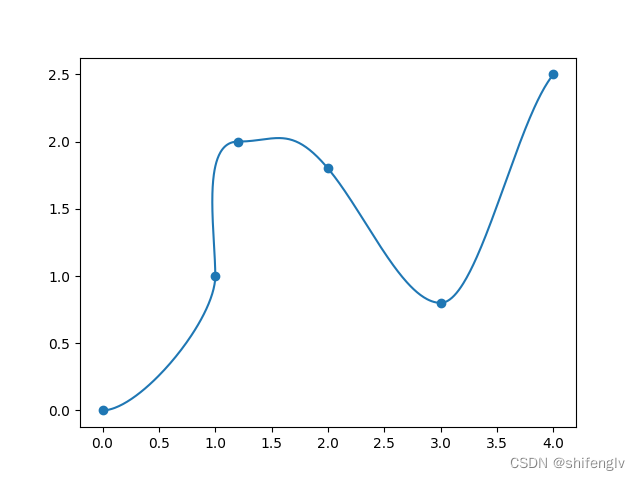
对于多点Hermite平滑,则是从头到尾,逐步取相邻的两个点,分别求出两点之间的Hermite曲线轨迹,比如,6个散点的Hermite曲线绘制的图像如下: