前言:最近发现我们项目组的成员因为不是gis的,很多都不懂经纬度偏移了以后应该怎么调整,调整多少合适,整理了一下,说一说。 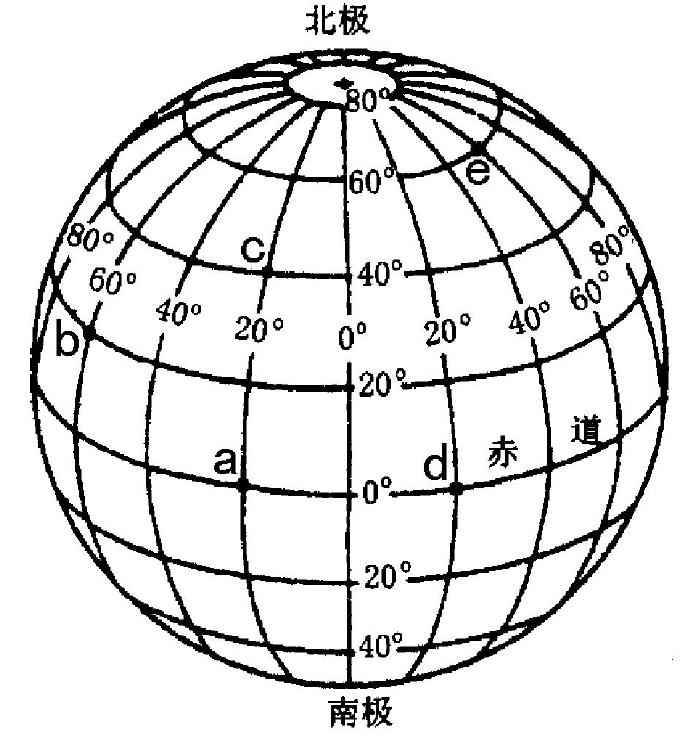
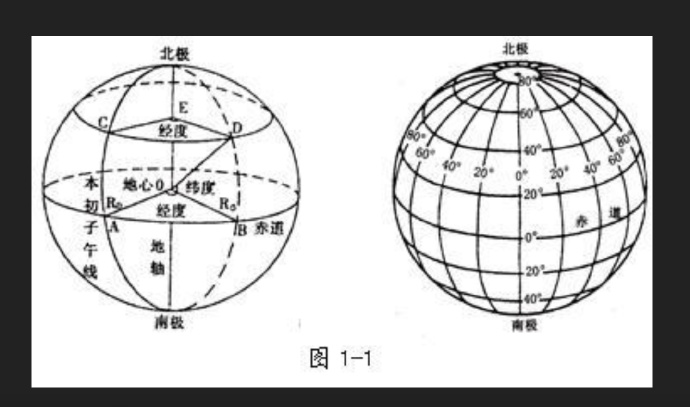
首先我们这里讨论的地球是正球,不考虑地球的实际形状,如果要考虑实际形状的话,得用微积分来解释,那就麻烦了,所以我们就用正球来解释。我们的地球是被经纬网包着的,如下图所示:

横纬竖经,从图中我们可以发现,经度每一圈都是长度相等的,都等于赤道周长。但纬度只有赤道最长,越靠近两极的地方周长越短。
基于以上的讲解,我们就可以明白,经度相差一度,距离是变化的,随着纬度的不同而不同。纬度相差一度,距离是固定的。我们这里先放上结论,推导过程稍后讲解。
一、纬度差1度对应的实际距离大约是111千米;
二、在赤道上经度差1度对应的实际距离大约是111千米;
三、在除赤道外的其他纬线上,经度差1度对应的实际距离是111*cosθ,其中θ表示纬度。
我们下面讲解推导过程,以赤道为例。
问题1:赤道的周长是多少?
答:我们知道圆的周长是2πR,赤道不就是个圆么,所以要算出赤道的周长,知道地球的半径就行了。那么地球的半径是多少呢?以WGS84坐标系为例,地球半径是6378137m,那么
赤道周长: 2*π*6378137=40,075,016.0019724
又因为赤道被分为了360度,所以一度就是
40,075,016.0019724/360=111,319.4888943678m≈111km
问题2:纬度相差一度是多少米?
答:根据问题1的讲解,相信这里不难理解了,也为111km。
问题3:经度相差一度是多少米?
答:赤道经度相差一度为111km,非赤道相差为111*cosθ。因为赤道的纬度值为0,cos0=1,所以 111 * 1 =111.
原理:上图

AB的距离是111,我们的目的是要求出CD的距离。因为三角形CED和AOB是相似三角形,所以求出ED和OB的关系,就可以得到AB和CD的关系了。
简单问题,我们把OEDB这个面单独拿出来,就形成了下面这个图: 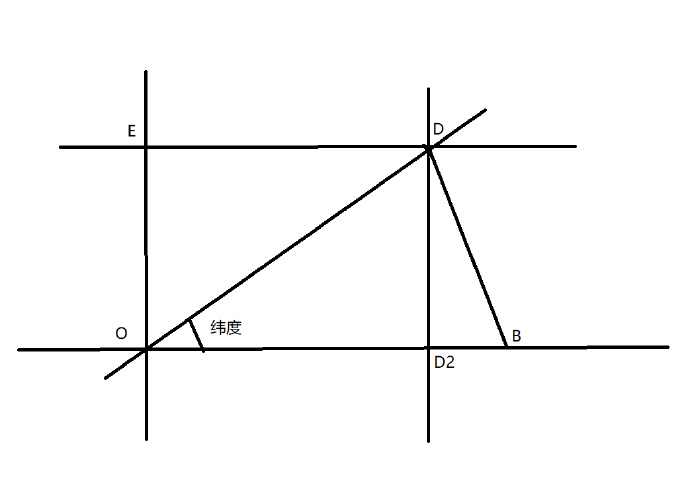

OEDD2是个正方形,由图可得,
ED=OD2,
又OD和OB都是地球半径,所以也相等,即
OD=OB
由上图可知,cosθ=OD2/OD=ED/OB,所以二者为cosθ的关系。那么根据相似三角形,AB和CD也是cosθ的关系,即CD=ABcosθ。又AB=111,所以CD=111cosθ,别忘了θ是纬度。
所以最终结论是:任意纬度上的经度差一度,相距都是111cosθ,只不过因为赤道的纬度是0,cos0=1,111*1=111,所以赤道上才是111,单位是km。