第一类换元积分法——凑微分法
假设现在我们要对一个复合函数f[g(x)] 求不定积分,但我只有∫f(x)dx=F(x)\int f(x)dx = F(x)∫f(x)dx=F(x) 这一积分公式。这时候就要想,要是中括号里不是g(x) 而是 x该多好啊。
如果我直接令u=g(x) ,强行让原式变为∫f(u)du\int f(u)du∫f(u)du 的话,就可以用积分公式了。
下面给出一些例题来进行具体说明:
例1:求 ∫e2x+1dx\int e^{2x+1}dx∫e2x+1dx
解:观察发现,这显然是一个复合函数,其内层函数为 u=2x+1 。那么我们可以考虑使用第一类换元法进行求解。
但容易发现,这个被积表达式并不符合条件。那我们不妨进行一下变形。
现在有了一个复合函数,只需要在后面乘上内层函数的导函数即可,即 ∫e2x+1.2dx\int e^{2x+1}.2dx∫e2x+1.2dx 但是为了等价,我们要给整体除以2,得到 12∫e2x+1.2dx\frac{1}{2}\int e^{2x+1}.2dx21∫e2x+1.2dx .
这下子我们可以用凑微分法了,把前面乘的2拿到微分符号后面d(2x),得到 ,但是为了方便积分,我们用它的等价形式d(2x+1) .
这样原式就变成了 12∫e2x+1d(2x+1)\frac{1}{2}\int e^{2x+1}d(2x+1)21∫e2x+1d(2x+1) .不妨令u=2x+1 ,则原式变为 12∫eud(u)\frac{1}{2}\int e^{u}d(u)21∫eud(u)
容易求得,结果为 12eu+C\frac{1}{2}e^{u}+C21eu+C
但是还没结束,我们要把变量换回去,即 12e2x+1+C\frac{1}{2}e^{2x+1}+C21e2x+1+C
即 ∫e2x+1dx\int e^{2x+1}dx∫e2x+1dx = 12e2x+1+C\frac{1}{2}e^{2x+1}+C21e2x+1+C
【结论1】当内层函数为线性函数[u=g(x)=ax+b ]时,原式可以按照下面的方法进行变形:
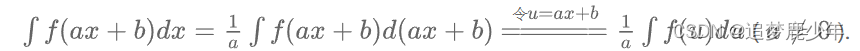

三角换元(第二类换元法)
第二类换元法的主要应用是利用带有平方的三角恒等式来去除被积函数中的根号。
要去除根号,无非就是两种方法:一是对根式平方;二是当根号下的式子是完全平方式时,把它开出来。显然,第一种方法无法做到在积分式子中等价变形,所以我们考虑第二种方法,构造出完全平方式[1]来去除根号。
注意到三角恒等式中,平方是经常出现的,比如:
sin2x+cos2x=1\sin^2 x +\cos ^2x =1sin2x+cos2x=1
sec2x=1+tan2x\sec ^2 x = 1+ \tan ^2 xsec2x=1+tan2x

求 ∫1x2−a2dx\int \frac{1}{\sqrt{x^2-a^2}}dx∫x2−a21dx


分部积分法
学完两种换元积分法以后,我发现学数学一定要有逆向思维的过程,也就是从某个过程的逆过程入手来研究某种运算。分部积分法就是这样得出的。

对(3)式变形就可以得到分部积分法的公式

为了方便做题,人们总结出了这样一句口诀:“反对幂指三”。口诀中的五个字分别对应了反三角函数、对数函数、幂函数、指数函数和三角函数。这个顺序正着就是不凑入微分符号的函数类型,逆着读就是优先凑入微分符号的函数类型。



有理函数的积分
首先我们来看一下什么是有理函数。所谓有理函数,其实就是两个仅由幂函数构成的多项式相除,比如 x2+3x−1\frac{x^2+3}{x-1}x−1x2+3,x2−2x+2x3−2x+1\frac{x^2-2x+2}{x^3-2x+1}x3−2x+1x2−2x+2 .当然,一个单独的幂函数也是有理函数。
如果要对上面一个相对复杂一点有理函数(比如上面的两个式子)进行积分,我们发现前面我们讲的方法都不能直接使用,也就是说,我们需要改变有理函数的形式,使其变成我们可以处理的形式再积分,而这个过程就是有理函数的积分。
对于一个分数,有真分数与假分数之分。同样的,对于一个分式,也有真分式与假分式之分。即,分子的最高次数小于分母的最高次数的分式为真分式,反之则为假分式。而假分式总是可以拆成真分式与多项式的和。
例如: x2+1x+1=x+1−x1+x\frac{x^2+1}{x+1}=x+\frac{1-x}{1+x}x+1x2+1=x+1+x1−x
而且,拆出来的那一个多项式是比较容易求积分的。这样我们就可以只分析有理函数中真分式的积分了。
真分式拆分:

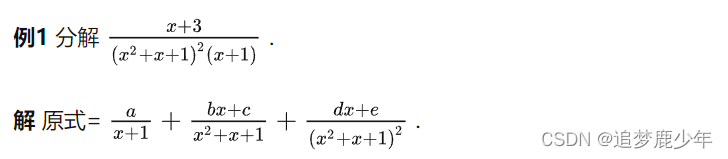
对于有理函数的积分,可以总结为一下几个步骤:
-
预处理,把假分式通过一定的手段化为多项式与真分式的和;
-
因式分解,把原式的分母进行因式分解,分解至分母中的因子最高次数为二次且不可继续分解;
-
拆分有理函数,按照讲的规则,把真分式拆成几个简单真分式的和;
-
求待定系数,常见的有通分并对比系数和留数法;
-
求解积分,通常会用到凑微分法。