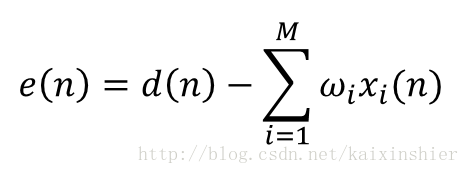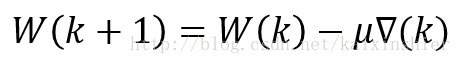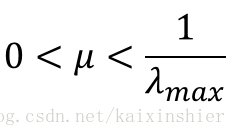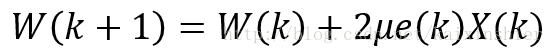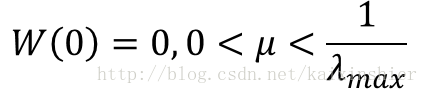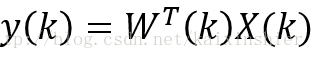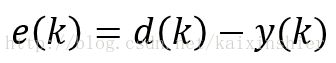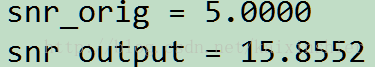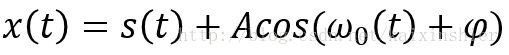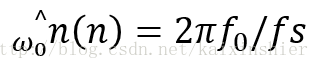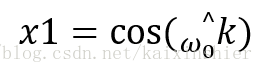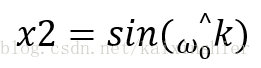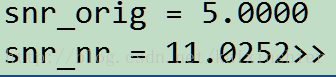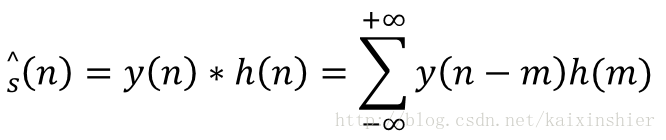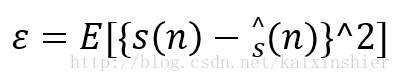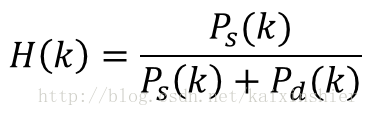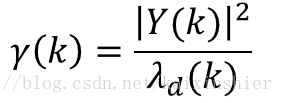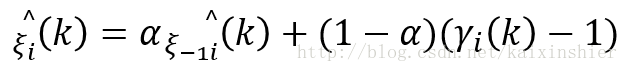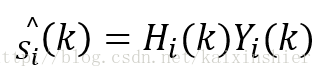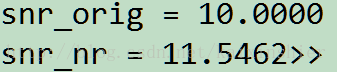文章为转载,原来地址:
http://blog.csdn.net/kaixinshier/article/details/72477679?locationNum=5&fps=1概述:现实生活中,语音信号一般都带有噪声,在进一步处理信号前(如语音识别,语音编码),往往要对信号进行降噪,本文介绍几种简单的降噪算法:自适应滤波器/谱减法/维纳滤波法。随着信噪比的减小,降噪方法处理的效果也随之变差,也经常使得语音丢字或者波形失真。如何在低信噪比情况下,达到不错的降噪效果,是一个值得探究的问题。
一. LMS自适应滤波器降噪
1.1. 基本原理
LMS自适应滤波器,利用前一刻已获得的滤波器参数,自动调节当前滤波器参数,以适应信号和噪声未知的或随机变化的统计特性,从而实现最优滤波。
1.2. 原理概述
输入信号序列xi(n),期望输出信号d(n),定义误差信号为:
其中wi为权系数。
LMS算法的本质就是寻找最优的权系数wi,使得误差信号e(n)最小。
经过一系列推导,得到权系数的迭代公式:
使用最陡下降法,那么LMS算法的关键问题就变为收敛因子μμ和梯度因子的求解。
(1). 收敛因子μμ控制收敛的速率,其取值范围:
其中λλ为相关矩阵的最大特征值。当它趋于无穷大,加权适矢量收敛于最优维纳解。
(2).梯度因子
近似计算得到梯度因子表达式:
因此权系数最终表达为:
1.3. 算法实施步骤
设定滤波器W(k)初值:
计算滤波器实际输出的估计值:
- 计算估算误差:
- 更新k+1时刻滤波器系数
- k变为k+1,重复步骤2-4
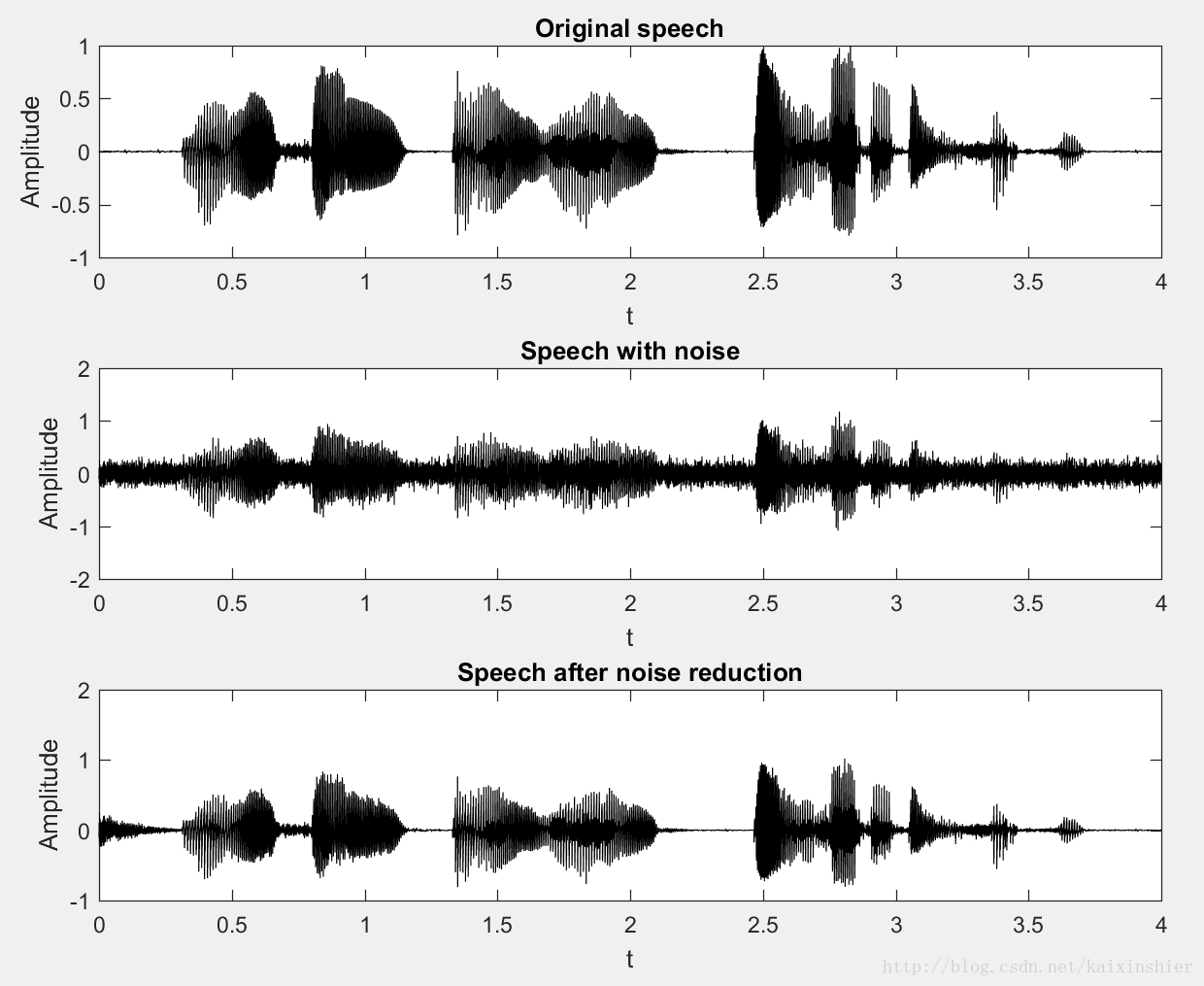
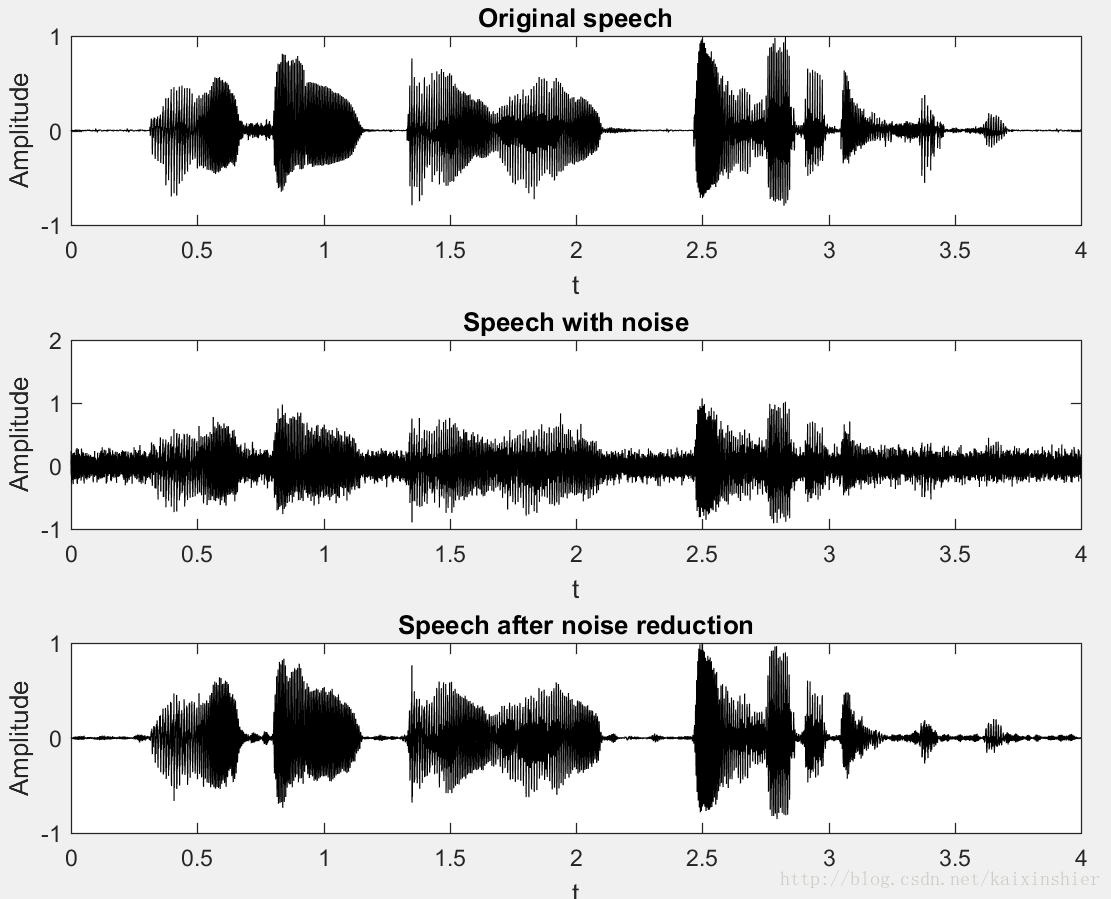
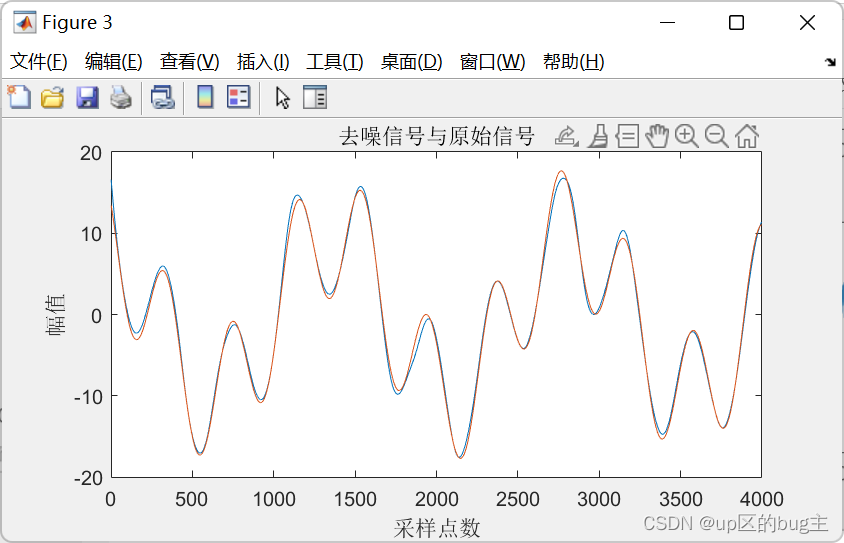
1.4. MATLAB仿真结果
说明: 加入白噪声信号,信噪比设定为snr = 5,降噪前后的信噪比为:
二. LMS的自适应陷波器
2.1. 基本原理
自适应陷波器法适用于单色干扰噪声,如单频正弦波噪声,希望陷波器的特性理想,缺口的肩部任意窄,可马上进入平坦区域。
2.2.原理概述
拿有两个权系数的滤波器为例,输入信号为纯语音和单频干扰的叠加:
采样后,
其中,
参考输入为标准正弦波和余弦波的叠加,
x1, x2可以构成任意幅度和相位的正弦波y(n)。
通过LMS自适应系数调整,使y(n)在幅度和相位与原始输入的单频干扰相同,从而清除单频干扰信号,达到陷波效果。
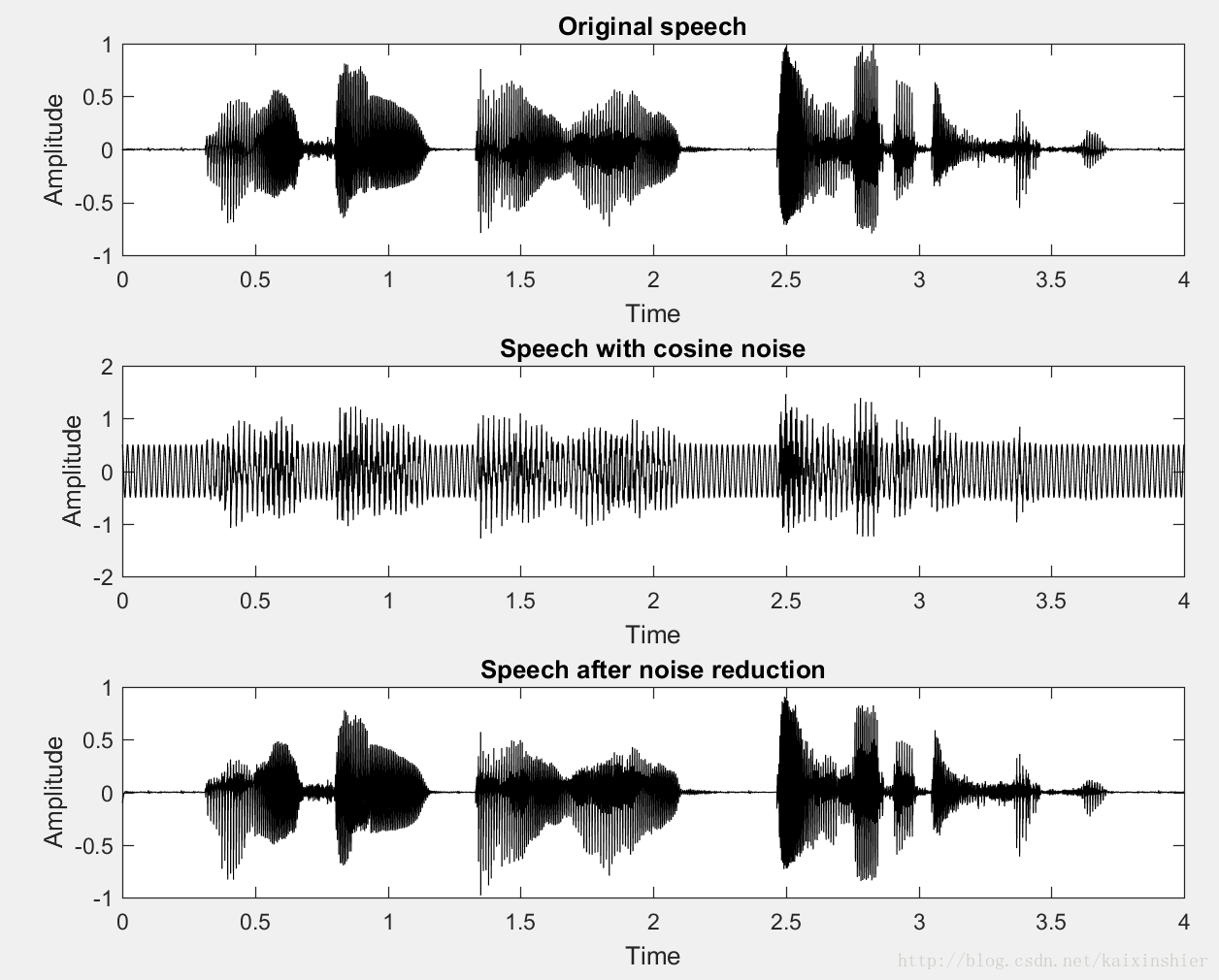
2.3. MATLAB仿真结果
说明:加入信噪比为snr = 5的单频噪声,滤波前后信噪比数值大小:
三. 基本谱减法
Tip: 由于基本谱减法带来明显噪声残留,需要进行算法改进。
3.1. 基本原理
语音信号处理最常用的方法,在频域进行降噪。
3.2. 算法步骤
语音信号对相位不灵敏,将谱减前的相位信息用到谱减后的信号中,在求出谱减后的幅值之后,结合相角,就能用IFFT求出谱减后的语音信号。
3.3. MATLAB仿真结果
说明:加入信噪比为snr = 5的白噪声,降噪后听到明显的噪声残留。
所以需要在谱减法的基础上做一些改进,传统的方法包括S.F.Boll提出的方法,E.Zavarehei根据其理论写了MATLAB函数 SSBoll79。具体细节这里就先不让谈。
四. 维纳滤波降噪
4.1. 基本原理
维纳滤波器降噪即设计一个数字滤波器h(n),使得输入的带噪语音信号与纯净语音信号的误差满足LMS准则
4.2. 当输入为y(n)时,滤波器输出为:
根据最小均方误差准则,要使得:
取极小值。
经过一系列推导,得到维纳滤波器谱估计器:
引入先验信噪比和后验信噪比,定义:
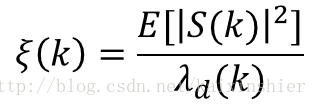
谱估计器可以进一步写成:
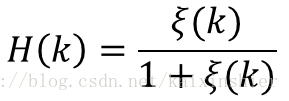
(基于先验信噪比的维纳滤波器谱估计器) 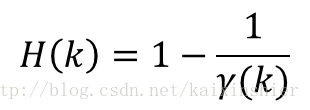
(基于后验信噪比的维纳滤波器谱估计器)
引入平滑参数得到先验信噪比和后验信噪比的关系:
表明由滴i-1帧的先验信噪比和第i帧的后验信噪比,就可求出第i帧的先验信噪比,一旦已知本帧的先验信噪比,就能导出本帧的维纳滤波器传递函数Hi(k)。 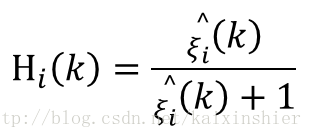
进一步可导出维纳滤波器的输出:
4.3. MATLAB仿真结果
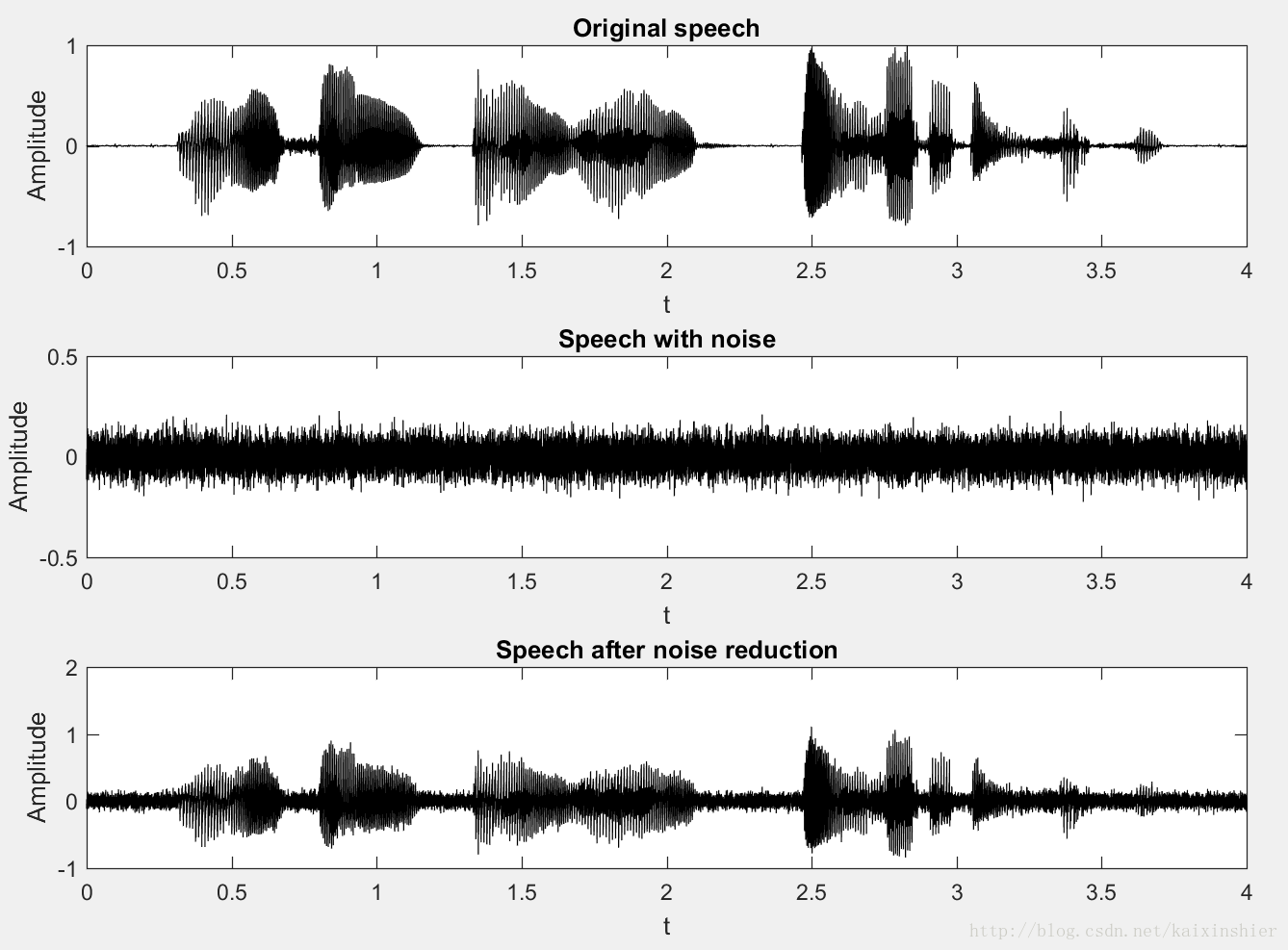
说明: 输入信噪比为10dB的白噪声,降噪前后的信噪比:
参考文献
[1]. 宋知用. Matlab在语音信号分析与合成中的应用[M]. 北京:北京航空航天大学出版社:2013.