一、定义
快速排序(英语:Quicksort),又称分区交换排序(英语:partition-exchange sort),简称「快排」,是一种被广泛运用的排序算法。
二、基本原理
- 快速排序是一个基于 分治 的排序方法。
给定一个数组 aaa,该数组共有 nnn 个元素,我们需要对其进行 从小到大(也可以从大到小)的排序。
假设要排序的区间为 [l,r][l,r][l,r]:
- 如果区间长度小于等于 1,那就直接退出(因为只有一个元素不用排序)。
- 否则在该区间中选择任意一个元素 xxx 作为 基准元素。将 大于xxx的元素放到 xxx 的 右边;将 小于xxx的元素放到 xxx 的 左边,等于 xxx 的元素随便放哪边。
- 此时,xxx 的位置实际上就已经确定了,再对 xxx 的左右两边的区间分别进行递归即可。
注意:为了保证时间复杂度,实际操作的时候,一般是随机选择区间的某一元素当作基准元素。
三、步骤与实现
1.步骤
在编写代码时,为了将 大于xxx 和 小于 xxx 的元素放到 xxx 的两边,我们并不需要使用额外的存储空间,只需要使用两个指针 iii 和 jjj。现在我们要对 区间[l,r][l,r][l,r]中的元素进行排序(我们这里选择第一个元素,即 a[i]a[i]a[i] 当作 xxx)。
- 初始的时候,i=l,j=ri = l , j = ri=l,j=r
- 首先,指针jjj 向左找到第一个 小于等于xxx 的元素,把它放到位置 iii 上;接着,指针 iii 向右找到第一个 大于等于xxx的元素,把它放到位置 jjj 上
- 一直重复这个过程,直到两个指针 iii 和 jjj 同时指向了同一位置 ppp,最后把位置 ppp 的值改为 xxx
- 此时对于区间 [l,r][l,r][l,r],元素 xxx 已经被放到了正确的位置 ppp 上
- 所以我们接下来只需要处理另外两个区间 [l,p−1][l,p - 1][l,p−1] 和 [p+1,r][p + 1,r][p+1,r],递归这个过程即可
2.代码实现
void quick_sort(int l,int r){//区间 [l,r] 的元素个数为 r - l + 1//如果区间元素个数 <= 1 就直接返回,即 r - l + 1 <= 1//化简一下就是 l >= rif(l >= r) return;//选择第一个元素当作 xint x = a[l];int i = l ,j = r;while(i < j){//先从右往左找到第一个 <= x 的元素while(i < j && a[j] > x) j--;//把找到的元素放到位置 i 上if(i < j) a[i++] = a[j];//再从左往右找到第一个 >= x 的元素while(i < j && a[i] < x) i++;//把找到的元素放到位置 j 上if(i < j) a[j--] = a[i];}//最后,i 和 j 同时指向了同一个位置 p//我们就把 a[p] 的值赋为 x//x 的位置就已经确定了a[i] = x;//再递归的处理剩下的两个区间,即 [l , p - 1] 和 [p + 1 , r]quick_sort(l,i-1);quick_sort(i+1,r);
}
我们可以试着完成一下,这道快速排序的模板题
完整代码:
#include <iostream>
#include <algorithm>using namespace std;const int N = 1e5+10;
int a[N];void quick_sort(int l,int r){if(l >= r) return;int x = a[l];int i = l ,j = r;while(i < j){while(i < j && a[j] > x) j--;if(i < j) a[i++] = a[j];while(i < j && a[i] < x) i++;if(i < j) a[j--] = a[i];}a[i] = x;quick_sort(l,i-1);quick_sort(i+1,r);
}int main(){int n;cin>>n;for(int i = 1;i <= n;i++) scanf("%d",&a[i]);quick_sort(1,n);for(int i = 1;i <= n;i++) printf("%d ",a[i]);return 0;
}点击提交之后,会发现有两个测试点 TLE了,也就是超时了。。。
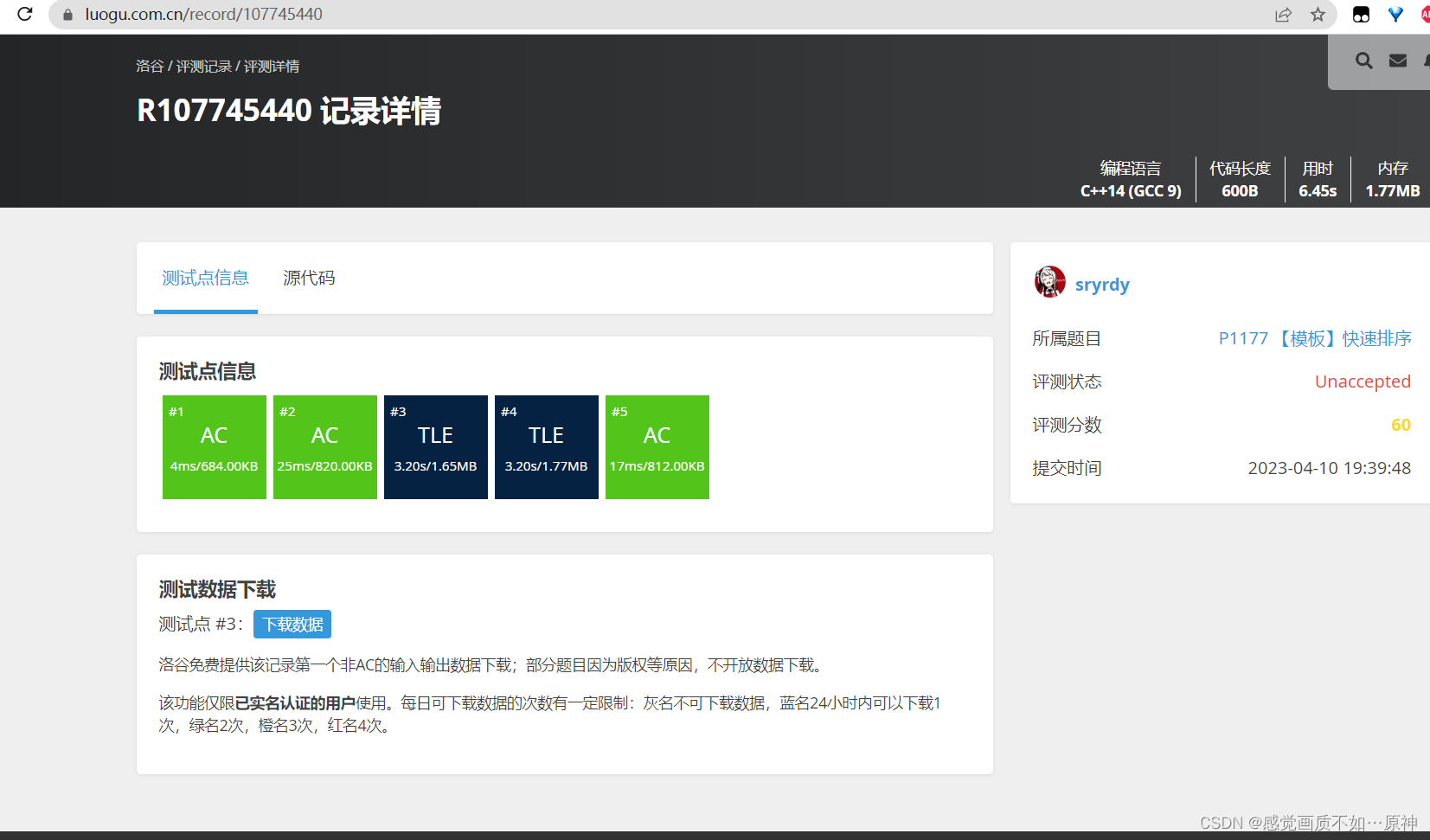
实际上快速排序的 平均时间复杂度是 O(nlogn)O(nlogn)O(nlogn)的,最坏时间复杂度是 O(n2)O(n^2)O(n2) 的。
上面我们提交的那份代码,就被这两个测试点的数据卡到了 O(n2)O(n^2)O(n2)。
题目的数据范围:
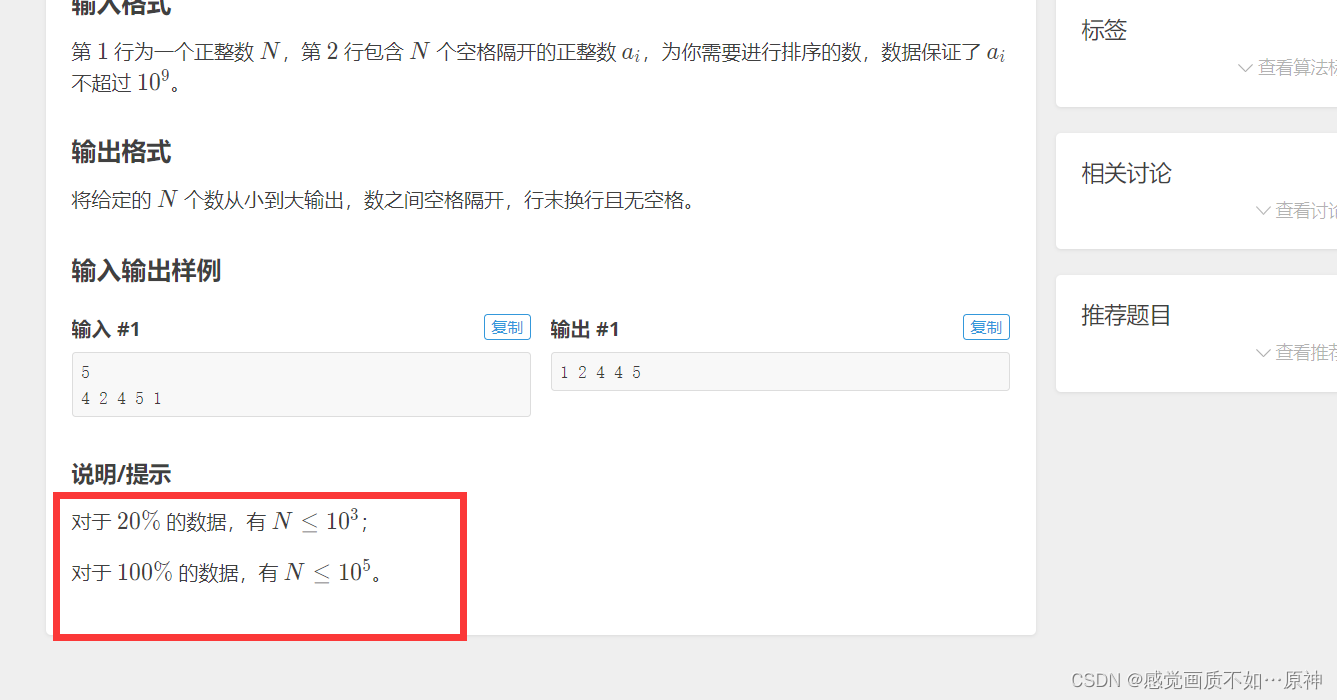
N最大是105,N2=1010N最大是 10^5,N^2 = 10^{10}N最大是105,N2=1010。一般的 OJ ,1s只能计算 10810^8108,所以肯定会超时。
为什么会被卡到 O(n2)O(n^2)O(n2) ?
我们试着对这个数组 a=[1,2,3,4,5,6,7]a = [1,2,3,4,5,6,7]a=[1,2,3,4,5,6,7] ,区间 [0,6][0,6][0,6] 进行排序。
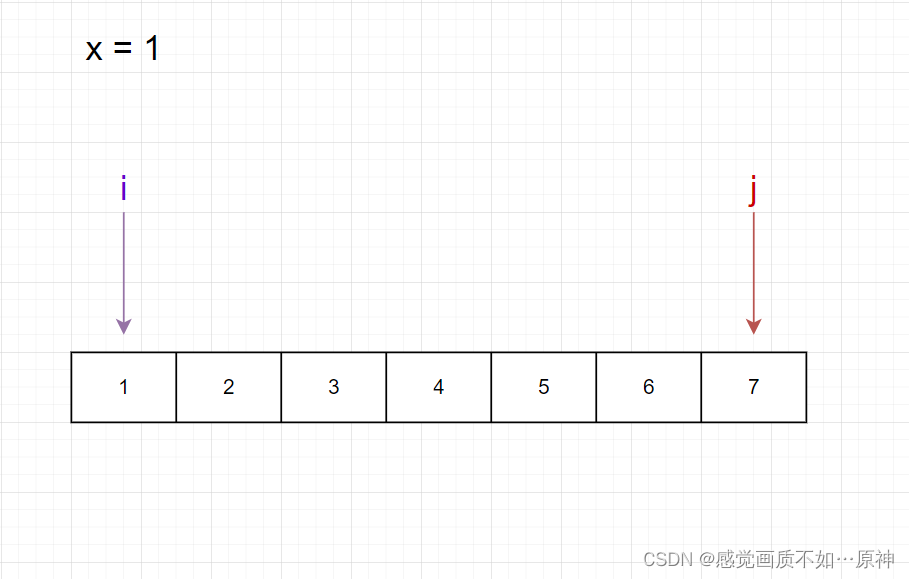
首先我们先要 从右往左 找到 第一个小于等于 111 的元素。
没有找到 小于等于 111 的元素,但是两个指针相遇了,111 的位置确定了。
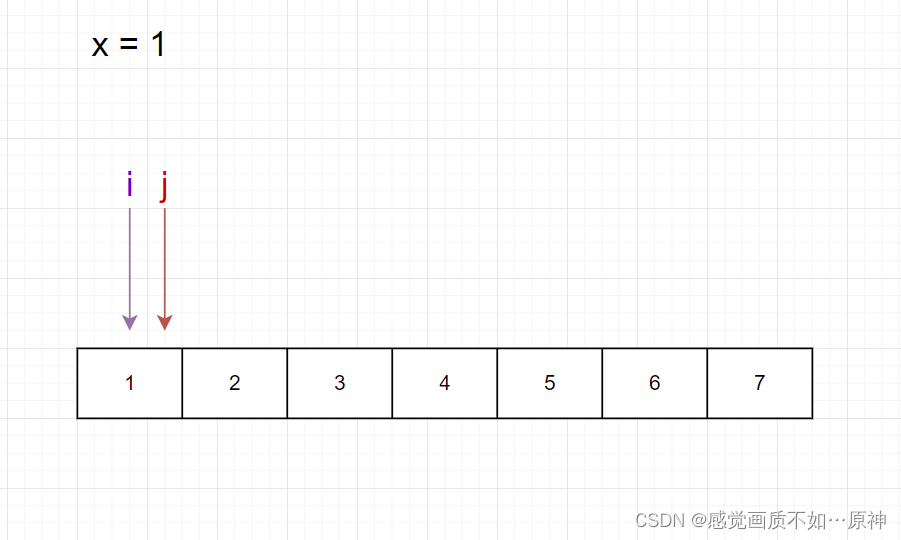
接下来对区间 [1,6][1,6][1,6] 的元素进行排序。
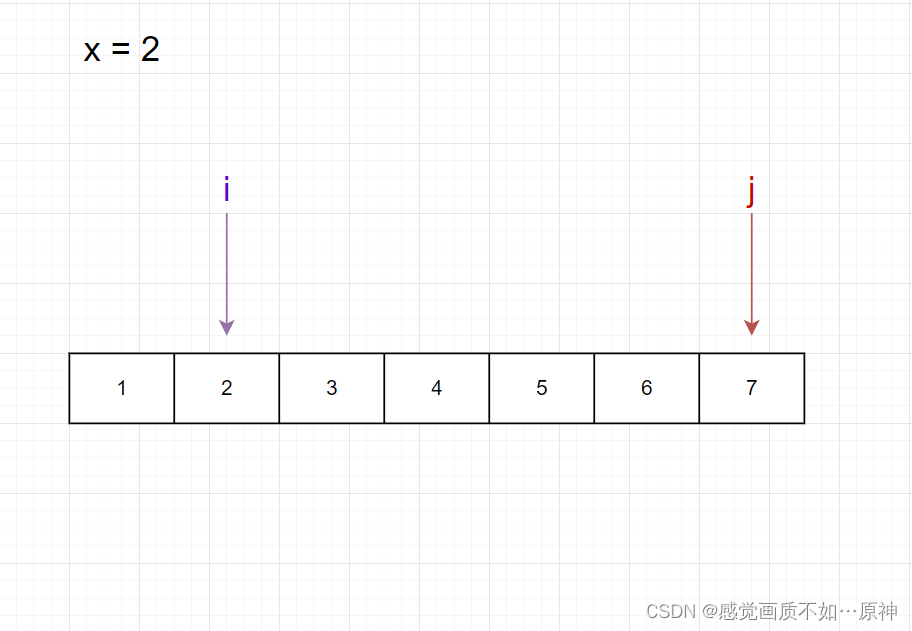
首先我们先要 从右往左 找到 第一个小于等于 222 的元素。
没有找到 小于等于 222 的元素,但是两个指针相遇了,222 的位置确定了。
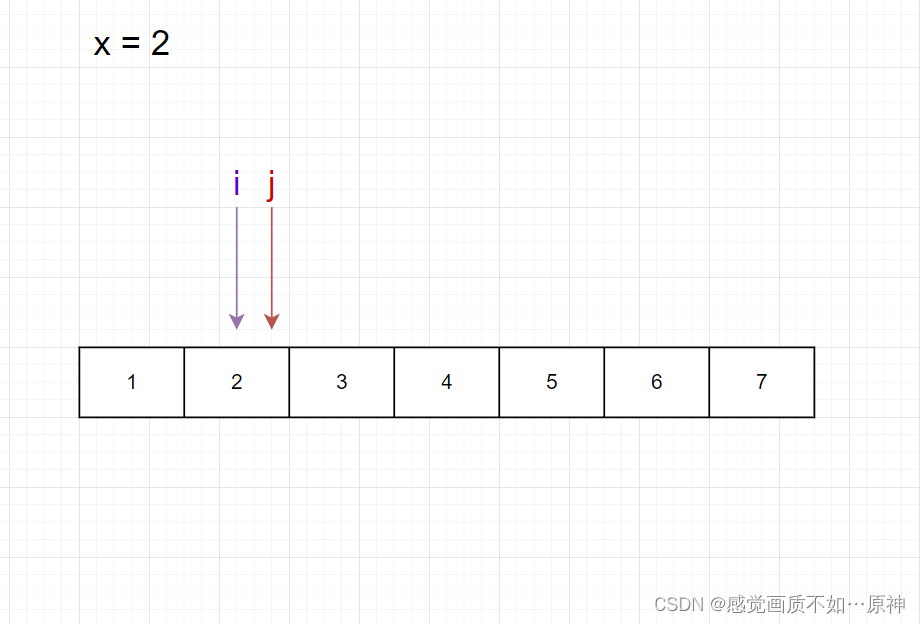
接下来对区间 [2,6][2,6][2,6] 的元素进行排序。

。。。。
我们发现对于 数组 a=[1,2,3,4,5,6,7]a = [1,2,3,4,5,6,7]a=[1,2,3,4,5,6,7] ,区间 [0,6][0,6][0,6],我们要递归的区间分别为:
- [0,6][0,6][0,6],指针移动的次数为6
- [1,6][1,6][1,6],指针移动的次数为5
- [2,6][2,6][2,6],指针移动的次数为4
- [3,6][3,6][3,6],指针移动的次数为3
- [4,6][4,6][4,6],指针移动的次数为2
- [5,6][5,6][5,6],指针移动的次数为1
总结:如果我们选择区间的第一个元素,也就是 a[l]a[l]a[l] 当作基准元素 xxx 的话。对于这种已经排好序的数组,再进行排序的话,一共会递归 n−1n - 1n−1 层。第一层指针扫过的次数为 n−1n - 1n−1;第二层指针扫过的次数为 n−2n - 2n−2;第三层指针扫过的次数为 n−3n - 3n−3.。。。
(n−1)+(n−2)+(n−3)+....+2+1=n(n−1)2(n-1) + (n-2) + (n-3) + ....+2 +1 = \frac{n(n-1)}{2} (n−1)+(n−2)+(n−3)+....+2+1=2n(n−1)
故,时间复杂度是 O(n2)O(n^2)O(n2)。
取区间的第一个元素作为基准元素 xxx 的话,是可以构造出一组数据直接把你卡成 O(n2)O(n^2)O(n2) 的。同理,取最后一个元素 或者是 取中间那个元素,也是可以构造出把你卡成 O(n2)O(n^2)O(n2) 的数据的。
正确的做法:对于区间 [l,r][l,r][l,r] ,我们应该是随机选择一个元素当作基准元素 xxx。
代码:
//随机选择swap(a[l] , a[l + rand() % (r - l + 1)]);int x = a[l];我们先将第一个元素 a[l]a[l]a[l] 和区间 [l,r][l,r][l,r] 中随机一个元素交换,再选择 a[l]a[l]a[l] 当作 xxx,这样就相当于直接从 [l,r][l,r][l,r] 中随机选择了一个元素。
正确的代码:
#include <iostream>
#include <algorithm>using namespace std;const int N = 1e5+10;
int a[N];void quick_sort(int l,int r){if(l >= r) return;//随机选择swap(a[l] , a[l + rand() % (r - l + 1)]);int x = a[l];int i = l ,j = r;while(i < j){while(i < j && a[j] > x) j--;if(i < j) a[i++] = a[j];while(i < j && a[i] < x) i++;if(i < j) a[j--] = a[i];}a[i] = x;quick_sort(l,i-1);quick_sort(i+1,r);
}int main(){int n;cin>>n;for(int i = 1;i <= n;i++) scanf("%d",&a[i]);quick_sort(1,n);for(int i = 1;i <= n;i++) printf("%d ",a[i]);return 0;
}这时我们再提交一次,就能够通过了。
四、一些细节问题
1.为什么是先从右往左找到第一个小于等于 xxx 的元素,再从左往右找到第一个大于等于 xxx 的元素?交换一下顺序行不行?
答案是不行。
用 a=[7,5,6,3,1,2,8]a = [7,5,6,3,1,2,8]a=[7,5,6,3,1,2,8] 举例。
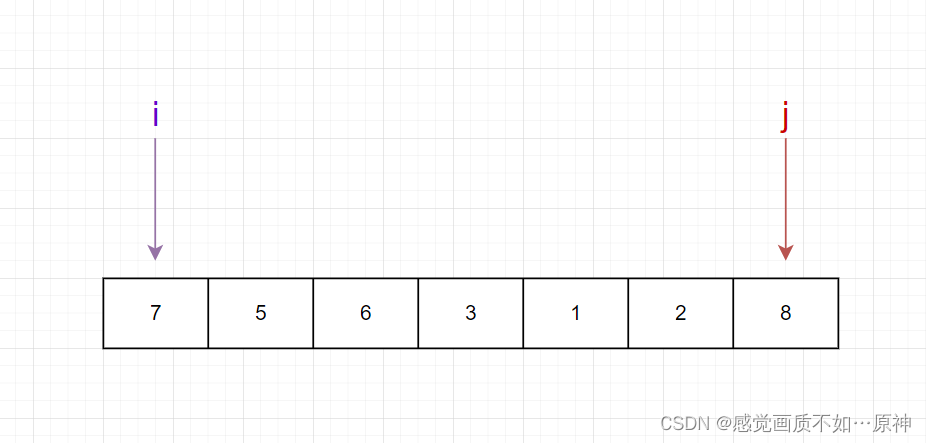
首先选择第一个元素 777 当作基准元素,相当于是从第一个位置拿出来了这个数,所以此时第一个位置相当于是空的。

首先 jjj 向左找到第一个 小于等于 xxx 的元素,放到位置 iii。

iii 再向右找到第一个大于等于 xxx 的元素,放到位置 jjj。
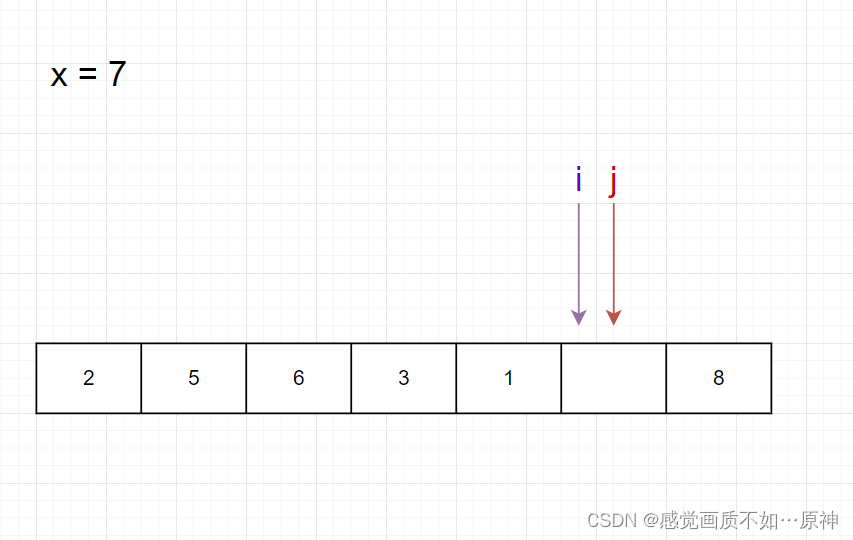
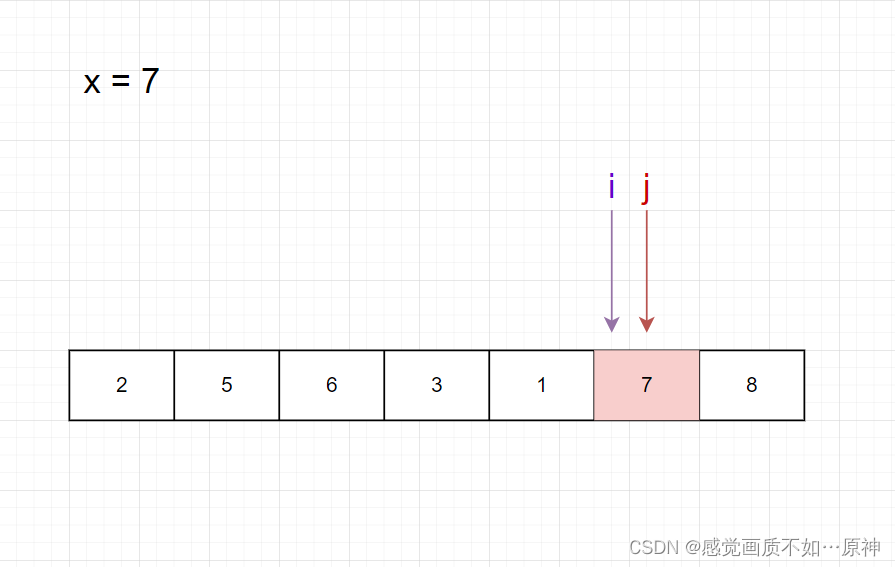
因为此时 iii 和 jjj 都指向了同一个位置,所以 a[i]=xa[i] = xa[i]=x。
此时位置 iii 左边的都是小于 xxx 的元素,位置 iii 右边的都是大于 xxx 的元素。
接着在递归左右两边,直到让整个数组变有序。
如果考虑先从左往右找到第一个大于等于 xxx 的元素,再从右往左找到第一个小于等于 xxx 的元素。
指针 iii 先从左往右找到第一个大于等于 777 的元素。
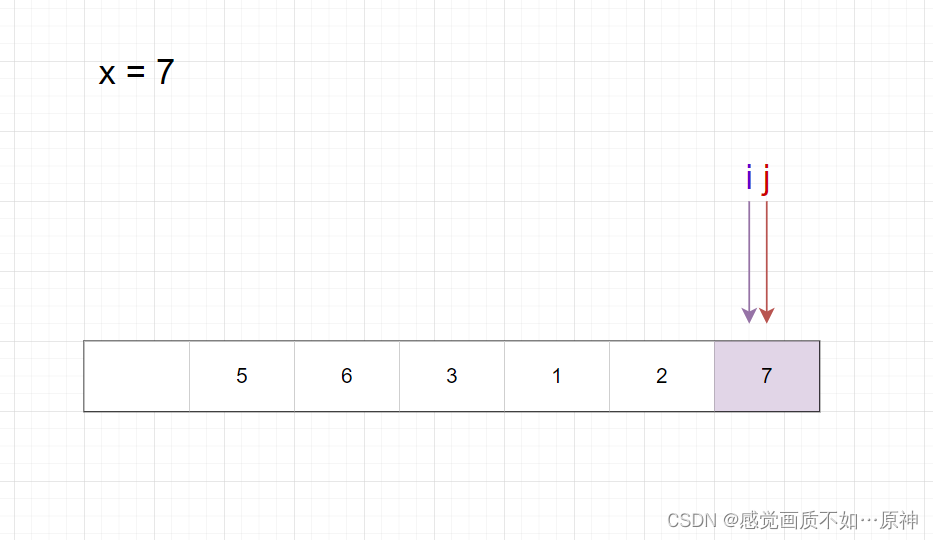
注意:这时,原来 a[j]=8a[j] = 8a[j]=8 这个数据就丢失了。
所以必须是 先从右往左找到第一个小于等于 xxx 的元素,再从左往右找到第一个大于等于 xxx 的元素。
1.为什么是从右往左找到第一个小于等于 xxx 的元素,再从左往右找到第一个大于等于 xxx 的元素?从右往左找到第一个小于 xxx 的元素,再从左往右找到第一个大于 xxx 的元素行不行?
答案是不行。
如果数组内的每个元素都不同,还不会出现问题。
如果数组内每个元素都相同,使用这组数据又会被卡成 O(n2)O(n^2)O(n2)。
可以自己举例子试一下。