MATLAB求解二维线性优化问题
- 前言
- 正文
- 函数实现
- 可视化结果
前言
二维线性优化问题指的是在二维空间中,对于一个由线性函数构成的目标函数,通过限制自变量的范围或满足特定的约束条件,寻找一个最优解(最小值或最大值)。这个问题可以用以下形式的数学模型来描述:
min/maxz=c1∗x1+c2∗x2subjectto:a1∗x1+a2∗x2<=b1a3∗x1+a4∗x2<=b2lb<=x1<=ublb<=x2<=ub\begin{equation}\begin{split} min/max z = c1*x1 + c2*x2\\ subject to: a1*x1 + a2*x2 <= b1\\ a3*x1 + a4*x2 <= b2\\ lb <= x1 <= ub\\ lb <= x2 <= ub \end{split}\end{equation} min/maxz=c1∗x1+c2∗x2subjectto:a1∗x1+a2∗x2<=b1a3∗x1+a4∗x2<=b2lb<=x1<=ublb<=x2<=ub
其中,x1x_1x1和x2x_2x2是自变量,c1c_1c1和c2c_2c2是常数,a1a_1a1、a2a_2a2、a3a_3a3、a4a_4a4、b1b_1b1和b2b_2b2也是常数,表示约束条件和目标函数的系数。最小化zzz表示寻找目标函数的最小值,最大化zzz表示寻找目标函数的最大值。在约束条件下,x1x_1x1和x2x_2x2的取值必须满足上下界(lblblb和ububub)的限制和不等式约束。在这个问题中,优化的目标是找到一组满足约束条件的自变量值,使得目标函数的值最小或最大。
粒子群优化(PSO)算法是一种基于群体智能的优化算法,它可以用于优化二维线性问题。以下是使用PSO算法解决二维线性优化问题的基本步骤:
- 定义适应度函数:将目标函数定义为适应度函数,即 f(x1,x2)=c1x1+c2x2f(x_1,x_2) = c_1x_1+c_2x_2f(x1,x2)=c1x1+c2x2。
- 初始化种群:设置粒子数量、位置范围、速度范围等参数,随机生成粒子的位置和速度。
- 计算适应度:根据粒子的位置计算适应度值。
- 更新全局最优解和局部最优解:根据适应度值更新全局最优解和局部最优解。
- 更新粒子速度和位置:根据当前位置和速度、全局最优解和局部最优解更新粒子的速度和位置。
- 检查终止条件:检查粒子的位置是否达到预设的最大迭代次数或适应度值是否达到预设的最小值,若满足则停止迭代,输出最优解。
在优化过程中,我们可以使用Matlab进行可视化操作,将优化过程和最终结果以图形化的方式展示出来,更直观地观察算法的运行情况和优化效果。
正文
下面我们使用粒子群优化算法求解下列二维线性函数的优化问题:
minf(x)=x12+x22−2x1−4x2+5minf(x) = x1^2 + x2^2 - 2x1 - 4x2 + 5 minf(x)=x12+x22−2x1−4x2+5
函数实现
% 设置PSO参数
num_particles = 100; % 粒子数量
num_iterations = 200; % 迭代次数
c1 = 1.5; % 学习因子1
c2 = 1.5; % 学习因子2
w = 0.7; % 惯性权重
lb = -10; % 自变量下限
ub = 10; % 自变量上限
n = 2; % 自变量个数% 初始化粒子群
particles = rand(num_particles, n) .* (ub - lb) + lb;
velocities = zeros(num_particles, n);
pbest = particles;
pbest_fitness = inf(num_particles, 1);
gbest = zeros(1, n);
gbest_fitness = inf;% 迭代PSO算法
for i = 1:num_iterations% 更新粒子速度和位置for j = 1:num_particles% 计算学习因子r1 = rand;r2 = rand;phi_p = c1 * r1;phi_g = c2 * r2;% 更新速度和位置velocities(j,:) = w * velocities(j,:) ...+ phi_p * (pbest(j,:) - particles(j,:)) ...+ phi_g * (gbest - particles(j,:));particles(j,:) = particles(j,:) + velocities(j,:);% 确保粒子位置在边界内particles(j,:) = max(particles(j,:), lb);particles(j,:) = min(particles(j,:), ub);end% 更新个体最优解和全局最优解for j = 1:num_particlesfitness = particles(j,1)^2 + particles(j,2)^2 - 2*particles(j,1) - 4*particles(j,2) + 5;if fitness < pbest_fitness(j)pbest(j,:) = particles(j,:);pbest_fitness(j) = fitness;endif fitness < gbest_fitnessgbest = particles(j,:);gbest_fitness = fitness;endend% 可视化当前迭代的粒子群和最优解scatter(particles(:,1), particles(:,2), 'k.');hold on;scatter(gbest(1), gbest(2), 'r*');hold off;title(sprintf('Iteration %d, Best Fitness: %g', i, gbest_fitness));drawnow;
end在上述代码中,我们设置了粒子数量为100100100,迭代次数为200200200。学习因子c1c1c1和c2c2c2分别设置为1.51.51.5,惯性权重www设置为0.70.70.7。
可视化结果
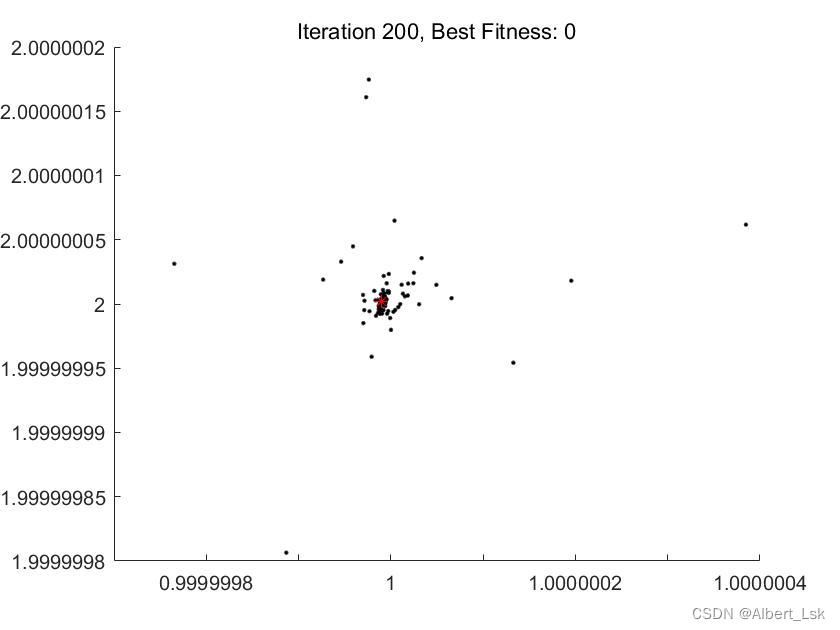
通过上图可知求解出的x1,x2x_1,x_2x1,x2分别为111和222。


![[论文速览] Sparks of Artificial General Intelligence: Early experiments with GPT-4](https://img-blog.csdnimg.cn/e7a12c37a257461989e266da30a93bc6.png)