目录
- 图灵机(turing machine)
- 例子
- 格局(configuration)
- Turing's Thesis
图灵机(turing machine)
学过计算机的人总归会多或少得听说过图灵机这种东西,但是图灵机究竟是什么呢?图灵机其实也是自动机的一种,并且图灵机会在状态转换过程中操作一个无限的tape
tape的样子如下图所示,tape里面包含字符,其中后面那个两竖一横的符号是blank的意思,它是一个特殊的字符,用来填满无限的tape
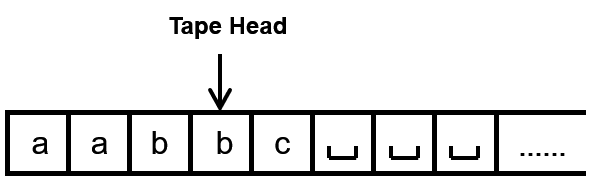
tape head指向当前tape上的字符
tape上的操作
- 可以对tape head指向的字符进行读/扫描操作
- 可以对tape head指向的字符进行写/更新操作
- 将tape head左移一格
- 将tape head右移一格
操作规则:
1、
每一步操作都要执行一下操作
- 读取当前的字符
- 更新当前格子中的字符
- 左移一格或者右移一格
如果当前tape指向最左边的格子,那么执行左移操作将不会发生移动
如果你不想更改当前格的字符,那么执行更新操作的时候只要让它更新为和当前字符一样即可
2、
操作行为类似于有限状态机
有初始状态
终止状态有两种:
- accept state
- reject state
计算结束后状态会变成下列三种中的一种:
- 终止并且接受(accept)
- 终止并且拒绝(reject)
- 循环(loop,就是说没有终止)
下面是图灵机的正式定义,Turing Machine可以表示为一个七元组 ( S , Σ , Γ , δ , s 0 , b , F ) (S,Σ,Γ,δ,s_{0},b,F) (S,Σ,Γ,δ,s0,b,F)
- S是一组状态的集合
- Σ Σ Σ是输入字母表
- Γ Γ Γ是tape的字母表
- δ δ δ是转换函数
- s 0 s_{0} s0是初始状态
- b b b是空符号
- F F F是终止状态的集合(包括accept或reject)
转换函数 δ δ δ定义为:
S × Σ → Γ × ( R / L ) × S S×Σ\rightarrow Γ×(R/L)×S S×Σ→Γ×(R/L)×S
这里的(R/L)就是执行左移或者右移操作,R就是向右(right)移动,L就是向左(left)移动
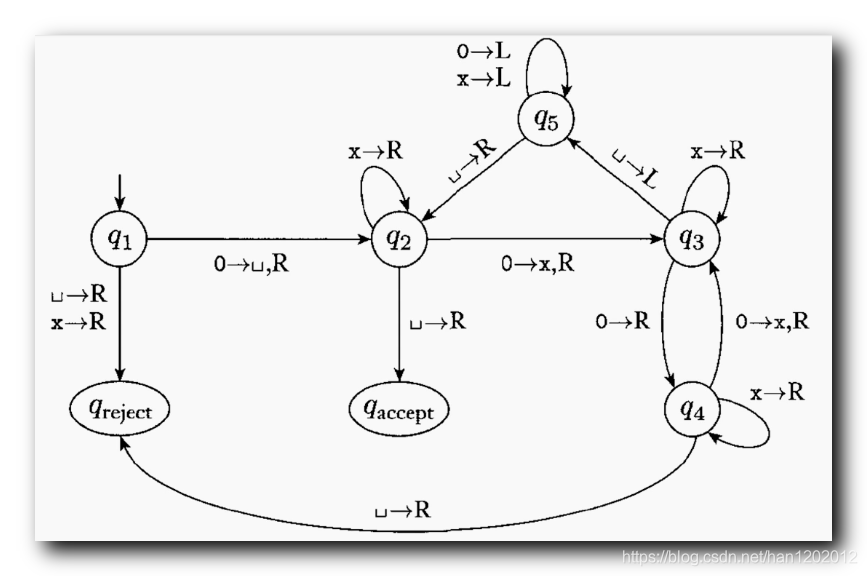
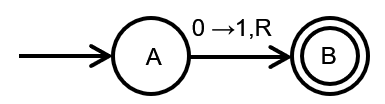
以下面这张图为例,在图上 0 → 1 , R 0\rightarrow 1,R 0→1,R代表的含义是,在状态A时接收字符0,那么将会转变为状态B,并且在当前磁头位置写下1这个字符,然后磁头向右移动一格
例子
接下来我们通过构建一个图灵机,并且实际运算一下,看看图灵机究竟是如何进行计算的
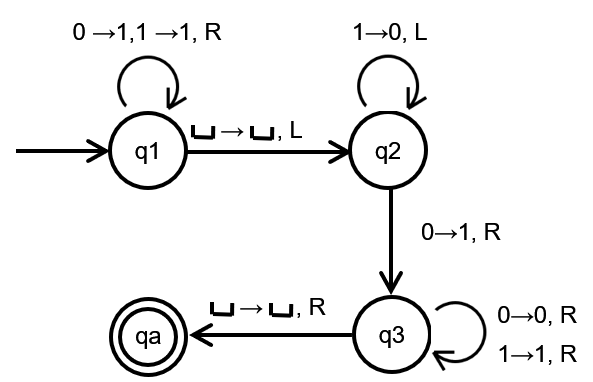
我们要构建图灵机,用于计算n+1函数,下图的初始状态是q1,结束状态是qa
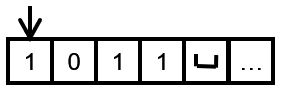
假设输入的数字为1011(二进制),初始时tape head指向第一个值
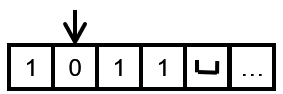
第一步读取一个1,自动机会通过 1 → 1 , R 1\rightarrow 1,R 1→1,R这个转换,转换后仍然变成 q 1 q_{1} q1,在第一格写入1,并将tape head右移一格
接下来的步骤和上面一样分别读取0,1,1仍然转变为 q 1 q_{1} q1,并且写上和原来相同的数字
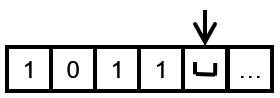
这时候的tape head指向了空字符,按照状态机的转换 q 1 q_{1} q1只能转变为 q 2 q_{2} q2,要注意的是,tape head会往左移动一格
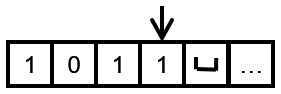
我们看看 q 2 q_{2} q2这边的转换,碰到1就写入0,并且向左移动tape head,因为按照二进制加法的逻辑,最后一位如果是1,那么+1后变成0,并且会进一位,如果最后一位是0,那么就直接变成1就行了,故此有了图上 q 2 q_{2} q2的转换
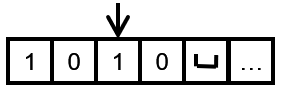
再执行一次上面的操作
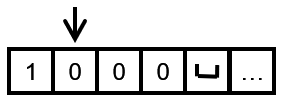
这次读取到了0,所以状态 q 2 q_{2} q2将会转变为 q 3 q_{3} q3,并且将0覆写为1,然后向右移动一格
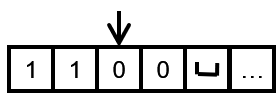
来到了 q 3 q_{3} q3状态,在这个状态下,只要单纯向右移动即可,因为写入的数字是相同的
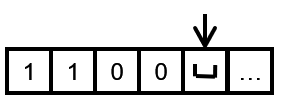
终于到了最后一步啦,看到读取空字符,然后 q 3 q_{3} q3状态就会转变为 q a q_{a} qa的接受状态,因为到达了终止状态,满足了图灵机的终止条件,所以图灵机运行完毕
我们来看看,我们输入的数字是1011,然后输出的数字是1100,所以我们实现的这个图灵机完成了n+1这个函数的操作步骤
格局(configuration)
configuration翻译成了格局,但这个东西其实就是一个图灵机在当前状态下的快照,由当前状态下tape中的字符,tape head指向的位置,以及当前自动机的状态这三个元素组成,可以简单的用如下图所示图灵机的格局
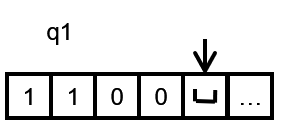
用字符串表示格局的话,是类似于下面这样的:
▹ \triangleright ▹ 1100 q 1 q_{1} q1 11001
▹ \triangleright ▹符号代表开始位置,里面的 q 1 q_{1} q1代表当前的状态,里面的字符代表的tape中的字符,tape head指向的是状态右边的第一个字符,所以在这个例子里面,tape head指向的是1
Turing’s Thesis
Turing’s Thesis
1、任何能被数字计算机执行的事情,Turing Machine同样也能够完成(从这里可以看出Turing Machine能力相当强大)
2、如果你能写出一个算法来解决某个问题,那么同样可以写出一个图灵机程序来解决相同的问题