前言

我正在刷卡哥的“代码随想录”，自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。
代码随想录此题链接

题目

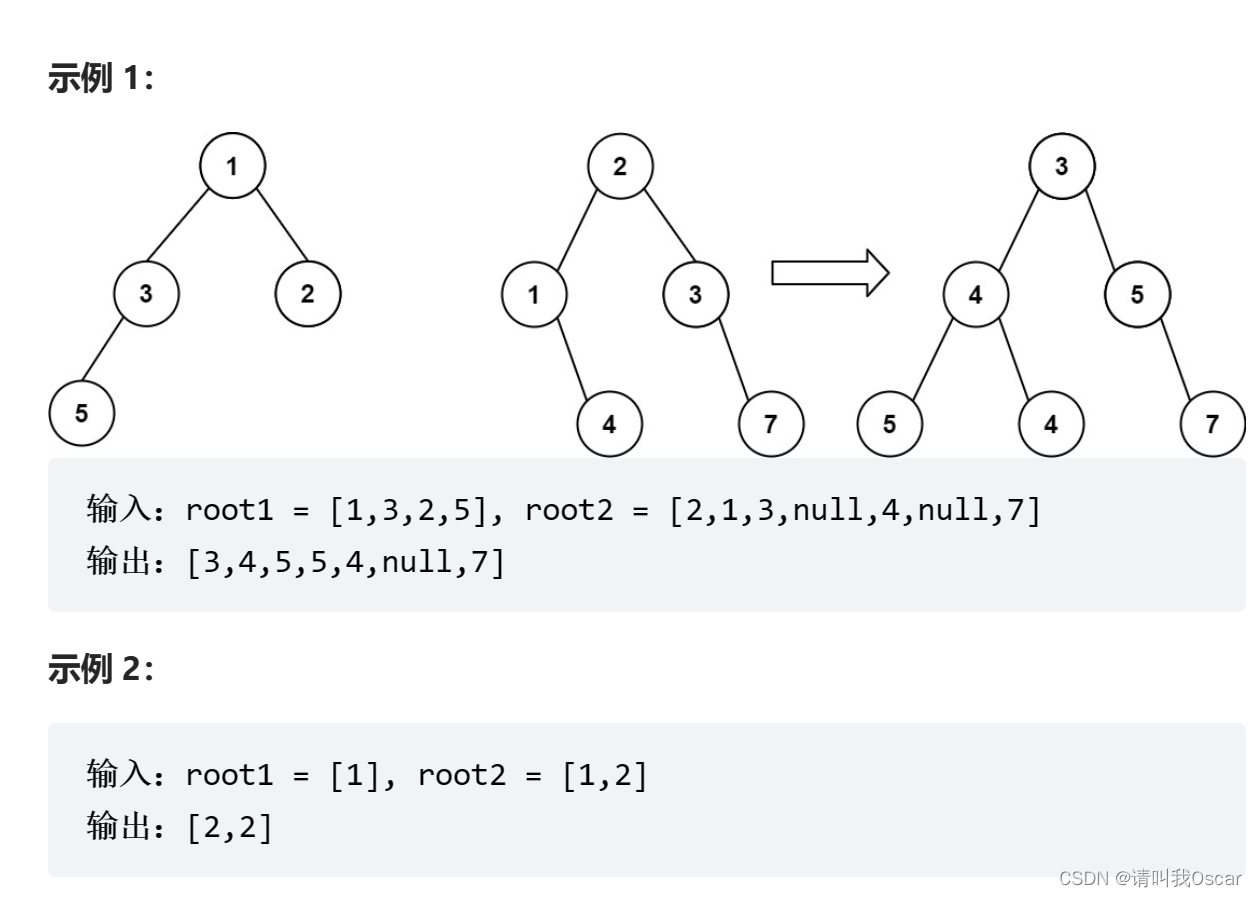
给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始

在这里插入图片描述

1.同时递归两棵二叉树（前序递归）

遍历两棵二叉树，如果第一棵二叉树的当前节点为空则返回第二棵二叉树的节点，反之则返回第一课的二叉树结点；
若两棵二叉树当前节点的都不为空则创建一个新的节点，节点的值为当前两棵二叉树当前的节点值之和。
新节点的左孩子分别递归两棵树当前节点的左孩子，
新节点的右孩子分别递归两棵树当前节点的右孩子，

2. 本题思路分析：

此题可以使用递归遍历，
三部曲：

第一步确定参数和返回值
参数：两棵二叉树的节点
返回值：当前节点
第二步截止递归的条件
当前第一棵树当前节点为空，返回第二棵树的当前节点，若第二棵树当前节点为空（此时第一棵树的节点不为空了）则返回第一棵树的当前节点。
第三步单层递归逻辑
将两棵树的当前节点之和相加，赋值给新建的树节点；
然后分别递归左右孩子节点分别给此新节点的左右孩子。

3. 算法实现

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {//前序遍历if(root1 == null){return root2;}else if(root2 == null){return root1;}TreeNode cur = new TreeNode(root1.val + root2.val);cur.left = mergeTrees(root1.left,root2.left);cur.right = mergeTrees(root1.right,root2.right);return cur;
}